
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С четырьмя неизвестными методом Гаусса.Содержание книги
Поиск на нашем сайте
Наиболее распространенным точным методом решения системы линейных уравнений является метод Гаусса. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему. Пусть дана произвольная система линейных уравнений:
........................................ а s 1х1+ а s 2х2+...+ аsпхп = bs. Будем производить над ней элементарные преобразования. Для этого выпишем матрицу из коэффициентов при неизвестных системы (1) с добавлением столбца свободных членов, другими словами расширенную матрицу Ā для системы (1):
Предположим, что с помощью таких преобразований удалось привести матрицу Ā к виду:
где все диагональные элементы b 11, b 22,..., brr отличны от нуля, а элементы, расположенные ниже диагональных, равны нулю. Матрице (3) соответствует система уравнений:
...................................... brrxr+...+brnxn=cr, которая получается из системы (1) с помощью некоторого числа элементарных преобразований и, следовательно, равносильна системе (1). Если в системе (4) r=n, то из последнего уравнения, имеющего вид bnnxn=cn (где bnn ≠ 0), находим единственное значение xn, из предпоследнего уравнения – значение xn-1 (поскольку xn уже известно) и т.д., наконец, из первого уравнения – значение x 1. Итак, в случае) r=n система имеет единственное решение. Если же r<n, то система (4) легко приводится к системе вида:
............................................ х r =a r, r +1х r +1+...+a r n х n +b r. которая и является по существу общим решением системы (1). Неизвестные х r+1,..., х n называются свободными. Из системы (5) можно будет найти значения х1,..., х r. Приведение матрицы Ā к виду (3) возможно только в том случае, когда исходная система уравнений (1) совместна. Если же система (1) несовместна, то такое приведение невозможно. Это обстоятельство выражается в том, что в процессе преобразований матрицы Ā в ней появляется строка, в которой все элементы равны нулю, кроме последнего. Такая строка соответствует уравнению вида: 0*х1+0*х2+...+0*х n = b, которому не удовлетворяют никакие значения неизвестных, так как b ≠0. В этом случае система несовместна. В процессе приведения системы (1) к ступенчатому виду могут получаться уравнения вида 0=0. Их можно отбрасывать, так как это приводит к системе уравнений, эквивалентных прежней. При решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя все преобразования над её строками. Последовательно получающиеся в ходе преобразований матрицы обычно соединяют знаком эквивалентности. Решим следующую систему уравнений с 4-мя неизвестными:
х1+3х2+2х3+х4=11, 2х1+10х2+9х3+7х4=40, 3х1+8х2+9х3+2х4=37. Выпишем расширенную матрицу из коэффициентов при неизвестных с добавлением столбца свободных членов.
Произведём анализ строк расширенной матрицы: - к элементам 2-ой строки прибавим элементы 1-ой, делённые на (-2); - из 3-ей строки вычтем 1-ю строку; - к 4-ой строке прибавим 1-ю, умноженную на (-3/2). В качестве вычислительного средства воспользуемся инструментами программы Excel– 97. 1. Включите компьютер. 2. Подождите пока загрузится операционная система Windows, после чего откройте окно MicrosoftExcel. 3. Заполните ячейки таблицы значениями расширенной матрицы (рис. 11.1)
Рис. 11.1 Рис. 11.2 4. Для выполнения выбранного словесного алгоритма производим следующие действия. · Активизируйте ячейку А5 и с клавиатуры занесите в неё формулу вида =А2+А1/(-2), после чего автозаполнением занесите численные результаты в ячейки В5¸Е5; · В ячейке А6 разместим результат вычитания 1-ой строки из 3-ей, и снова, пользуясь автозаполнением, заполним ячейки В6¸Е6; · в ячейке А7 запишем формулу вида =А4+А1*(-3/2) и автозаполнением занесём численные результаты в ячейки В7¸Е7. · Далее скроем 2, 3 и 4 – строки, которые нам уже не нужны. Для этого воспользуемся пунктом меню ФОРМАТ®СТРОКА®СКРЫТЬ (см.§ 6). Результат показан на рис. 11.2. 5. Снова произведём анализ строк получившихся в результате элементарных преобразований матрицы, чтобы привести её к треугольному виду. ·К 6-ой строке прибавим 5-ю, умноженную на число (-10); ·из 7-ой строки вычтем 5-ю. Записанный алгоритм реализуем в ячейках А8, А9, после чего скроем 6 и 7 – строки (см. рис. 11.3).
Рис. 11.3 Рис. 11.4 6. И последнее, что нужно сделать, чтобы привести матрицу к треугольному виду – это к 9-ой строке прибавить 8-ю, умноженную на (-3/5), после чего скрыть 9-ю строку (рис. 11.4). Как вы можете видеть, элементы получившейся матрицы находятся в 1, 5, 8 и 10 строках, при этом ранг получившейся матрицы r = 4, следовательно, данная система уравнений имеет единственное решение. Выпишем получившуюся систему: 2х1+5х2+4х3+ х4 =20, 0,5х2 + 0,5х4=1, 5х3+х4 =10, -0,6х4=0. Из последнего уравнения легко находим х4=0; из 3-го уравнения находим х3=2; из 2-го – х2=2 и из 1-го – х1=1 соответственно.
Задания для самостоятельной работы.
Методом Гаусса решите системы уравнений:
Лабораторная работа № 15. Нахождение корней уравнения f(x)=0
Методы решения линейных и квадратных уравнений были известны еще древним грекам. Решение уравнений третьей и четвертой степеней были получены усилиями итальянских математиков Ш. Ферро, Н. Тартальи, Дж. Картано, Л. Феррари в эпоху Возрождения. Затем наступила пора поиска формул для нахождения корней уравнений пятой и более высоких степеней. Настойчивые, но безрезультатные попытки продолжались около 300 лет и завершились в 20-х годах ХХ1Х века благодаря работам норвежского математика Н. Абеля. Он доказал, что общее уравне6ие пятой и более высоких степеней неразрешимы в радикалах. Решение общего уравнения n-ой степени a0xn+a1xn-1+…+an-1x+an=0, a0¹0 (1) при n³5 нельзя выразить через коэффициенты с помощью действий сложения, вычитания, умножения, деления, возведения в степень и извлечения корня. Для неалгебраических уравнений типа х–cos(x)=0 (2) задача еще более усложняется. В этом случае найти для корней явные выражения, за редким случаем не удается. В условиях, когда формулы «не работают», когда рассчитывать на них можно только в самых простейших случаях, особое значение приобретают универсальные вычислительные алгоритмы. Известен целый ряд алгоритмов, позволяющих решить рассматриваемую задачу.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 2022; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.98.0 (0.006 с.) |

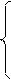 а11х1+ а12х2+...+ а1пхп = b 1,
а11х1+ а12х2+...+ а1пхп = b 1,

 b11x1+b12x2+...+b1rxr+...+b1nxn=c1,
b11x1+b12x2+...+b1rxr+...+b1nxn=c1, х1=a1, r +1х r +1+...+a1 n х n +b1,
х1=a1, r +1х r +1+...+a1 n х n +b1, 2х1+5х2+4х3+х4=20,
2х1+5х2+4х3+х4=20,








