Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа №2. Определители 3-го порядка и их вычисление.Содержание книги
Поиск на нашем сайте
Для введения понятия – определитель третьего порядка рассмотрим систему трёх линейных уравнений с тремя неизвестными: a11x1+ a12x2+ a13x3=b1 a21x1+ a22x2+ a23x3=b2 (1) a31x1+ a32x2+ a33x3=b3 Чтобы найти х1 умножим уравнения системы (1) соответственно на а22а33 - а32а23, а32а13-а12а33, а12а23-а22а13 и сложим получаемые левые и правые части. После приведения подобных членов (относительно х1, х2 и х3) окажется, что коэффициенты при х2 и х3 равны нулю. Предполагая, что коэффициент при х1 отличен от нуля, получим:
Составим таблицу чисел из коэффициентов при неизвестных х1, х2 и х3 системы (1):
Эта таблица чисел называется квадратной матрицей 3-го порядка (у неё три строки и три столбца). Выражение, стоящее в знаменателе формулы (2), можно составить из чисел матрицы А по следующему правилу. Произведение чисел, расположенных на главной диагонали, и два произведения чисел, расположенных в вершинах двух равнобедренных треугольников с основанием, параллельным главной диагонали, и с вершиной в противоположном углу, берутся со знаком плюс. Три произведения, которые строятся по такому же правилу, но относительно второй диагонали, берутся со знаком минус. Составленная таким образом сумма шести слагаемых (из которых три взяты со знаком плюс, а три – со знаком минус) называется определителем 3-го порядка матрицы А и обозначается через:
Итак, знаменатель в формуле (2) представляется в виде определителя ½ A ½. Что касается числителя, то, поскольку он получается из знаменателя заменой a11, a21, a31 соответственно на b1, b2, b3, то его можно представить в виде определителя
Аналогичным образом, если уравнения системы (1) умножим последовательно на а31а23 - а21а33, а11а33-а31а13, а21а13-а11а23 и результаты сложить, то найдём формулу для х2. Наконец, умножая уравнения (1) последовательно на а21а32 - а31а22, а31а12-а11а32, а11а22-а21а12, найдём формулу для х3.
Окончательно будем иметь:
где матрицы А 1, А 2, А 3 получаются из А заменой соответствующего столбца на свободные члены. Формулы (3) известны как формулы Крамера. Они получены задолго до появления современных информационных технологий и представляют пример формализации метода исключения неизвестных к алгоритму решения системы (1), подлежащему реализации средствами информационных технологий.
Итак, понятие определитель возникло в процессе получения метода решения линейных алгебраических уравнений, который был бы удобен для так называемого машинного счёта. Теперь для реализации процесса вычисления определителя 3-го порядка на базе современных информационных технологий, вернёмся к следующей формуле вычисления определителя
Формула (4) представляет математический алгоритм. Изложим программу реализации алгоритма, определяемого формулой (4) с использованием программ Word – 95 (97,2000), Калькулятор и Excel-95 (97, 2000), функционирующих в операционной системе Windows 95 (98, 2000). Для этого необходимо конкретизировать алгоритм, например, применительно к заданному определителю
Формулу (5) необходимо прежде всего переписать на экран компьютера. Для чего необходимо войти в текстовый редактор Word, после выполнения следующих операций. 1. Включите компьютер. 2. Подождите пока загрузится операционная система Windows, после чего откройте окно Microsoft Word. 3. Вставьте объект Microsoft Equation3. 0. 4. Перепишем формулу (5) в формульном редакторе. Для этого: · Вставьте шаблон определителя 3-го порядка в формульном редакторе: выполните нажатие ЛКМ в ШАБЛОНЕ СКОБОК на шаблон · Занесём числовые значения элементов определителя в свободные поля (§1, рис.9). Процесс заполнения свободных полей числами будем осуществлять с помощью клавиатуры. Для этого: · нажмите на клавишу с цифрой 4, после чего цифра 4 появится в свободном поле верхнего левого угла; · нажмите на клавишу Tab (активным станет поле, располагающееся справа от поля с цифрой 4); · нажмите на клавишу с изображением знака «-» и на клавишу с цифрой 3; · нажмите на клавишу Tab, после чего активным станет поле в верхнем правом углу; · нажмите на клавишу с изображением цифры 5; вся верхняя строка определителя окажется заполненной; · нажмите на клавишу Tab (активным станет поле, находящееся под цифрой 4, т.е. вторая строка определителя), где в такой же последовательности заполните вторую строку определителя цифрами 3, -2, 8 и третью цифрами 1, -7, 5. Таким образом, чтобы перейти из одного свободного поля в другое нужно воспользоваться клавишей Tab, а заполнять свободные поля значениями нужно при помощи цифровых клавиш.
& Далее, в тексте задачника будем обозначать: занесите числовые значения определителя (матрицы) в свободные поля.
5. Для записи правой части формулы (5) на экране необходимо: · после того, как будет заполнено последнее поле цифрой 5, два раза нажмите на клавишу Tab; · нажмите на клавишу с изображением знака «=»; · нажмите на клавишу с изображением цифры 4; · выполните нажатие ЛКМ на шаблон ОПЕРАТОРЫ (см. рис. 2.1) и выберите шаблон вида Таким же образом продолжим запись формулы (5) для вычисления определителя. В итоге на экране компьютера получим запись всего алгоритма (5) (рис.2.3):
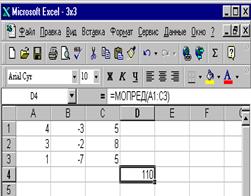
Рис. 2.3 Итак, программа Word нам позволил записать весь математический алгоритм (5) без использования бумаги и ручки, чем обычно пользуются в школе при решении задач линейной алгебры. 6. В качестве вычислительного средства воспользуемся программой Калькулятор. Для этого: ·выполните нажатие ЛКМ на кнопке ПУСК; ·в открывшемся меню передвигайте указатель мыши вверх до тех пор, пока не окажется подсвеченным пункт меню ПРОГРАММЫ, далее СТАНДАРТНЫЕ и затем КАЛЬКУЛЯТОР. Если калькулятор имеет вид обычного калькулятора (рис.2.4), то выполните нажатие ЛКМ на пункте Вид в строке меню ·выполните нажатие ЛКМ на пункте Инженерный.
Рис. 2.4 Рис.2.5 На экране монитора появится изображение инженерного калькулятора (рис. 2.5). ·Для удобства счёта перетащите калькулятор под формулу (рис.2.3) так, как это показано на рис. 2.6. 7. · выполните нажатие ЛКМ на цифре 4; · затем на знак * (знак умножения); · далее выполните нажатие ЛКМ на кнопку с изображением скобки (; · · выполните нажатие ЛКМ на кнопку с изображением скобки) и т.д. Таким образом, все вычисления на данном калькуляторе будут проводиться так же, как и на обыкновенном при условии, что нажимать на цифры нужно при помощи левой кнопки мыши (щёлкая указателем мыши на нужные цифры и кнопки), а отрицательные числа (числа со знаком минус) брать в скобки. ·После того, как на калькуляторе будет набрана формула (5), нажмите на знак «=» калькулятора и получится результат равный 110 (рис. 2.6). Итак, поставленная задача по вычислению определителей 3-го порядка решена программными средствами двух программ Word и Калькулятор. Программа Калькулятор не очень сильное вычислительное средство, так как он не обладает макро – средствами, позволяющими вычислять значение определителя в полностью автоматическом режиме. Однако, с методической точки зрения она очень полезна при решении несложных вычислительных задач, так как благодаря прозрачности промежуточных вычислений пользователь осваивает числовые расчёты. 8. Быструю проверку проделанных вычислений можно сделать в программе Excel, обладающей большими возможностями. Для этого: · заполните ячейки таблицы Excel значениями элементов определителя: A1=4, B1= -3, C1=5, A2=3, B2= -2, C2=8, A31, B3= -7,C3=5 (рис. 2.7). · Воспользуемся мастером функций, который располагается в стандартной панели инструментов и имеет значок вида a) активизируйте ячейку D4; b) вызовите мастер функций, выполнив нажатие ЛКМ в стандартной панели инструментов на кнопке fх; c) В появившемся окне КАТЕГОРИЯ выберите МАТЕМАТИЧЕСКИЕ нажатием ЛКМ, а в окне ФУНКЦИЯ - МОПРЕД, после чего выполните нажатие ЛКМ на ОК (см. рис. 2.8);
После того, как мы щёлкнем мышью по кнопке ОК, на мониторе появится окно второго шага вычисления определителя (рис. 2.9).! ( Если появившееся окно закроет определитель, то нужно сдвинуть его. Для этого:
 
· разместите указатель мыши в любом месте окна; · выполните нажатие ЛКМ и, не отпуская, переместите в нужное место с тем, чтобы стал виден определитель). · Выполните нажатие ЛКМ на 1-й элемент определителя, который находится в ячейке А1 и перетащите указатель мыши по главной диагонали до ячейки С3 (рис.2.9).
Рис. 2.9 Рис. 2.10 · Выполните нажатие ЛКМ на кнопке ОК. & Далее, в тексте задачника будем обозначать: воспользуйтесь функцией..., которая находится в мастере функций ƒх. Результат вычислений появится в ячейке D4 (см. рис. 2.10), который подтверждает правильность предыдущих вычислений. Из методических соображений, очевидно, что если при изучении темы: Определители 3-го порядка в качестве вычислительного средства достаточно применения программы калькулятор, то при решении систем алгебраических уравнений по формулам (3) с целью ускорения вычислительных процедур необходимо использовать программу Excel для вычисления определителей по описанной выше технологии, написанной на входном языке программы Excel.
Задания для самостоятельной работы. Вычислите следующие определители.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 359; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.151.89 (0.011 с.) |






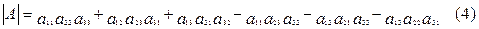

 , а в ШАБЛОНЕ МАТРИЦ на шаблон
, а в ШАБЛОНЕ МАТРИЦ на шаблон  .
.
 Рис. 2.1 Рис. 2.2
Рис. 2.1 Рис. 2.2 ; результат представлен на рис.2.2.
; результат представлен на рис.2.2.
 ;
;

 После придания экрану компьютера вид рис. 2.6 можно приступать к расчёту величины определителя. Для чего:
После придания экрану компьютера вид рис. 2.6 можно приступать к расчёту величины определителя. Для чего: затем на знак «—» и на цифру 2;
затем на знак «—» и на цифру 2; . Для этого:
. Для этого: