
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для создания таблицы удобно использовать уже готовую таблицу, используемую в предыдущей работе.Содержание книги
Поиск на нашем сайте
а) Сделайте еще одну копию Листа1. б) На новом листе вставьте новые столбцы там, где это необходимо. Для этого выделите столбец G и выполните два раза команду ВСТАВКА-СТОЛБЦЫ. в) Измените заголовок таблицы, так что бы он имел вид как на рисунке.
3. Возьмем в качестве шага
В ячейки А2, A3, А4 запишите значения, соответствующие отрезку интегрирования [3;5] и величине шага 0,25: 3;5, 0,25. В ячейке А5 рассчитайте число отрезков разбиения n по формуле
4. В столбец В введем значения Для этого в ячейку В2 введем 0; в ячейку B3 введем 1; выделим ячейки B2 и B1 и протянем их до ячейки В10 с помощью маркера заполнения. 5. Вычисление значений аргумента.
В ячейку С2 запишите формулу Excel: =A2 и нажмите Enter. В ячейке С2 появится значение нижнего предела интегрирования. В дальнейшем, при изменении числового значения в ячейке А2, будет изменяться число и в ячейке С2. В ячейку СЗ запишите значение следующей точки разбиения по формуле Excel: =С2+А4 и закрепите в ней адрес шага h - ячейку А4. Для этого дважды щелкните мышью в строке формул на адресе А4, чтобы выделить его, и нажмите клавишу F4. После этого адрес ячейки А4 станет абсолютным, на что указывает символ $ перед буквой столбца и номером строки адреса. Формула примет вид =C2+$А$4
В дальнейшем, при переносе формулы адрес А4, в отличие от адреса C2, меняться не будет. Перенесите формулу ячейки С3 вниз до десятой строки с помощью маркера заполнения. После выполнения этого действия столбец С таблицы будет заполнен значениями точек разбиения отрезка [3;5].
6. Вычисление значений функции.
В ячейке D2 запишите формулу Excel: =КОРЕНЬ(6+C2^4), по которой рассчитывается значение функции в точке C2. Для этого выделите ячейку D2 и, нажав ƒх на панели инструментов, выполните команду ВСТАВКА ФУНКЦИИ. Выберите категорию функций математические, далее функцию КОРЕНЬ, в строке «число» наберите 6+C2^4. Перенесите эту формулу ячейки D2 вниз до десятой строки с помощью маркера заполнения. После выполнения этого шага в столбце D таблицы окажутся значения функции во всех точках разбиения.
7. Перенесем, полученные в столбце D значения, в ячейки столбцов E и F. Для этого необходимо скопировать значения в ячейках столбца D, сделать активной ячейку E1, выполнить команду меню Правка-Специальная вставка, в диалоговом окне выбрать пункт Значения.
Далее в столбце D оставим только значения в ячейках D2 и D10 в столбце E – значения в ячейках E3, E5, E7, E9
8. В ячейках D12, E12, F12 подсчитаем сумму значений, расположенных в соответствующих столбцах. Для этого воспользуемся функцией СУММ (которая находится в мастере функций ƒх) или кнопкой автосуммы
9. Вычисление приближенного значения интеграла.
В ячейке G2 вычислите приближенное значение интеграла по формуле
После выполнения этого шага в ячейке G2 появится результат приближенного вычисления интеграла c шагом h = 0,25.
10. Вычислим интеграл по формуле Симпсона еще раз, беря удвоенный шаг 2 h =2∙0,25 = 0,5. При этом будем использовать данные столбцов D, E, F.
Поскольку мы увеличили шаг в 2 раза, то число отрезков разбиения уменьшилось в 2 раза и теперь В ячейке H2 запишите формулу Excel: =A4*2/3*(D12+4*(F4+F8)+2*F6). После выполнения этого шага в ячейке H2 появится результат приближенного вычисления интеграла c шагом h = 0,5.
11. Оценка погрешности вычисления. По правилу Рунге, абсолютная погрешность результата Выделите ячейку I2 и запишите формулу Excel: =ABS(H2-G2)/15. Для этого воспользуемся функцией ABS (которая находится в мастере функций ƒх). Абсолютная погрешность результата В результате выполненных шагов получится таблица:
Задание. Вычислить приближенно, пользуясь формулой Симпсона, определенный интеграл Определить погрешность метода по формуле
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.183.187 (0.009 с.) |


 . При этом
. При этом  .
. , т.е. запишите формулу Excel: =(А3-А2)/А4. В результате отрезок интегрирования окажется разбитым на 8 частей.
, т.е. запишите формулу Excel: =(А3-А2)/А4. В результате отрезок интегрирования окажется разбитым на 8 частей.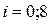 .
.


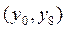 ;
; ; в столбце F – значения в ячейках F4, F6, F8
; в столбце F – значения в ячейках F4, F6, F8  .
. на панели инструментов.
на панели инструментов. , т.е. запишите формулу Excel: =A4/3*(D12+4*E12+2*E12).
, т.е. запишите формулу Excel: =A4/3*(D12+4*E12+2*E12).
 .
.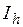 приближенно равна
приближенно равна  .
. . Замечание. Если бы d оказалось > 0,005, пришлось бы заново провести расчет с шагом
. Замечание. Если бы d оказалось > 0,005, пришлось бы заново провести расчет с шагом  .
.
 , разбивая отрезок интегрирования на 12 равных частей. Затем вычислить интеграл, разбив отрезок интегрирования на 6 частей.
, разбивая отрезок интегрирования на 12 равных частей. Затем вычислить интеграл, разбив отрезок интегрирования на 6 частей. .
.


