Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа №17. Анализ экономико-исторических явлений статистическими моделямиСодержание книги
Поиск на нашем сайте Известно, что историческая наука должна не только фиксировать во времени факты из жизни общества, но и устанавливать причинно - следственные связи, приводящие к тем или иным историческим явлениям. Процесс анализа причинно – следственных связей должен основываться на количественных соотношениях, отражающих сущность исторических явлений. В таком случае указанный анализ будет беспристрастным, т.е. исключающим субъективизм того или иного исследователя. Переход к беспристрастному анализу исторических фактов связан с их формализацией, т.е. установлению количественной меры того или иного явления и последующим представлением характера явления в форме математического закона. Для иллюстрации принципа формализации исторических явлений рассмотрим данные об аграрном развитии 50 губерний Европейской России на рубеже XIX - XX веков (табл.1) Таблица 1
Данная таблица обладает только тем свойством, что названия губерний представлены в алфавитном порядке, а данные по количеству десятин посевной земли на душу населения представлены в хаотическом виде. Из этих хаотически представленных данных невозможно установить их влияние на ход исторических процессов в Европейской части России. Обозначим через x «посев на душу в десятинах» эту величину примем в качестве количественного признака губерний. Если сгруппировать губернии из таблицы 1 по числовым значениям этого признака, то после выявления общих исторических событий внутри сгруппированных указанным образом губерний можно установить влияние признака х как причины на характер тех или иных исторических событий. Этот анализ можно произвести с использованием программы MS Excel. Для проведения указанного анализа фактические данные таблицы 1 необходимо ввести в память ПК. Это можно сделать вводом данных с клавиатуры, но это трудоемко. Во избежание ошибок при ручном вводе с клавиатуры произведем сканирование таблицы 1 ▲ Ввод данных с помощью FineReader Процесс ввода данных можно частично автоматизировать, для чего необходимо воспользоваться сканером и программой по распознаванию текста. Самой распространенной такой программой является продукт компании ABBYY под названием FineReader. Предпочтительно использовать поздние версии: 5.0, 6.0 или выше. Процесс оцифровки изображения текста и его распознавания можно условно разделить на ряд макроэтапов: 1. Запуск FineReader 2. Ввод изображения – сканирование. Процесс сканирования в общих чертах похож во всех типах интерфейсов сканеров. Как правило, он состоит из 3 этапов: Þ Предварительное сканирование – делается с целью определения области сканирования и его параметров (разрешение, муар, цветность и проч.) В случае многостраничного сканирования (одинаковые параметры страницы) первый макроэтап остается одинаковым для всех сканов. Þ Собственно сканирование – сканирование с рабочими параметрами выделенной области изображения Þ Экспорт или сохранение полученного изображения данных. В нашем случае осуществляется автоматический экспорт данных в FineReader 3. Сегментация изображения и определения его принадлежности к определенной категории. В нашем случае это таблица
4. Распознавание изображения.
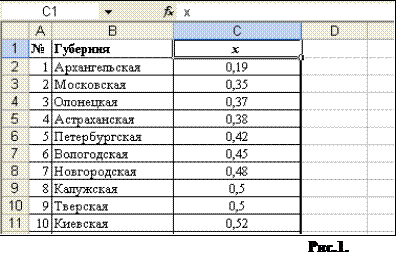
Возможно, полученные данные будут нуждаться в правке вследствие ошибок в распознавании. (рис. 1)
Введенный список ранжирован по возрастанию признака x в столбце С рабочего стола программы Excel (Лист 1) величины x изменяются от минимального xmin =0,19(ячейка С2) до максимального xmax =1,95(ячейка С51). Теперь весь ряд числовых значений
Для вычисления d в ячейку D1 введем формулу: =(F51-F2)/10. Нажмем Enter. После чего в ячейке D1 получим значение d равное 0,176.
Переходим на Лист 2 Excel. В ячейку А1 помещаем символ i, означающий номер интервала, в ячейки – B1 и С1 символ d, в ячейку D1 - символ x Для автоматического заполнения столбца А (Лист 2) необходимо ввести в ячейку А2 значение 1, в ячейку А3 значение 2. Затем выделить ячейки А2 и А3 и, «ухватившись» курсором за маркер виде черного квадратика
Теперь нам необходимо создать первую последовательность d, которая представляет собой числовую последовательность и 10 членов, где каждое последующее число больше предыдущего на величину d, а первый член равен 0,19. Для реализации этого необходимо внести в ячейку B2 значение 0,19, а в B3 формулу: =$B$2+(Лист1!$D$1*Лист2!A2). Примените автозаполнение до ячейки B11. В синтаксисе формулы встречается значок $ -этот условный символ в Excel означает придание свойства неизменности параметру, стоящего после него. Эта неизменность проявляется при использовании функции автозаполнение. Проследив зависимость в формуле, можно понять алгоритм вычислений. Вторая последовательность d (столбец С) аналогична первой за исключением того, что она начинается со значения 0,366, и ссылка на ячейку в формуле изменилась: =$ С $2+(Лист1!$D$1*Лист2!A2) (с В на С). Перейдем к последовательности xi (столбцу значений D). Последовательность будет представлять собой ряд средних арифметических значений из столбцов В и С по строке. Для реализации этого алгоритма внесём в ячейку D2 формулу: =(B2+C2)/2 иприменим автозаполнение до ячейки D11. Число xi называют статистическим числом, так как оно эквивалентно всем числам попадающим в i -ый интервал. Для вычисления чисел ni (столбец Е) необходимо осуществить счет числа губерний, попадающих в i -ый интервал. Чтобы осуществить расчет мы воспользуемся алгоритмом, состоящим из нескольких шагов. ▲ Алгоритм расчета числа значений, попадающих в определенный интервал Шаг 1. Выделим ячейки С2:С11 на Лист2 («:» условно обозначает интервал ячеек). Выполним операцию копирования воспользовавшись, например, «горячими» клавишами Ctrl+C («+» - одновременное нажатие). Щёлкнем по ячейке С13 правой клавишейи в появившемся контекстным меню выберем «Специальная вставка». В появившемся окне «Специальная вставка» выберем в поле«Вставить» радиокнопку значения. В поле «Операция» поставим галочку транспонировать. Столбец С2:С11 превратился в строку C13:L13. Назовем этот метод методом транспонированной вставки. Шаг 2. Перейдем на Лист 1. В ячейку Е2 внесём формулу: =ЕСЛИ(Лист2!C$13>=Лист1!$C2;1;0). Формула определяет значение ячейки 1, в случае если ячейка С13 больше или равна ячейке С2, в противном случае 0. Вставленные символы $ в формулу позволят нам применить функцию автозаполнения, сохраняя необходимый нам адрес ячейки. Применим функцию автозаполнения сначала в интервале E2:N2, а затем, сохранив выделение, протащим его вниз до ячейки N51. (Рис. 2)
Шаг 3. Выделим ячейку Е52 и нажмем значок суммы Рис.3
Таким образом, мы получили значения для ni.
Выделим ячейку E12 нажмем значок суммы
Вычисление частот pi попадения губерний в i -ый интервал осуществляется по формуле
Для реализации этого, введём в ячейку F2 формулу: =E2/E$12. Применим автозаполнение до ячейки F11. (Рис.4) Рис.4
Здесь столбцы D и F представляют ряд распределения статистической величины xi, т.е. таблицу значений этой величины и частоты pi их появления. Указанный ряд распределения характеризуется математическим ожиданием:
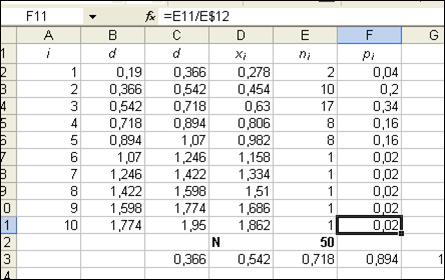
и средним квадратическим отклонением равным
В случае нормального закона распределения статистической величины x Величина же
▲Вычисление значений Шаг 1. Для вычисления математического ожидания – величины С этой целью внесём в ячейку G1 обозначение столбца «xi*Pi». В ячейку G2 внесём формулу: =D2*F2, применим автозаполнение до ячейки G11. Для вычисления Шаг 2. Вычисление Ø Вячейку Н1 введёмобозначение столбца Ø В ячейку Н12 введём формулу: =КОРЕНЬ(СУММ(H2:H11)) – расчет корня из суммы по столбцу Н. Получившийся результат – значение (Рис.5).
Столбцы D и Е (рис. 5) позволяют табличный ряд распределения статистической величины представить графически в виде так называемого многоугольника распределения. ▲ Построение многоугольника распределения статистической величины. Для этого: Ø Нажмем значок Мастер диаграмм В поле Тип выберем третий вариант, в Вид – четвертый. Шаг 1 из 4. (рис.6) Рис. 6
Ø
Нажимаем Далее. В поле Диапазон укажем: =Лист2!$F$2:$F$11 (можно просто выделить на листе). Перейдем на вкладку Ряд. В поле Подписи оси X укажем: =Лист2!$D$2:$D$11 (можно просто выделить на листе). Шаг 2 из 4. (Рис. 7).
Ø Нажимаем Далее. Переходим на закладку Заголовки. В поле Название диаграммы внесем: Многоугольник распределения случайной величины. Внесём обозначение осей xi и pi. На закладке Легенда снимем галочку Добавить легенду. Шаг 3 из 4. Ø Нажимаем Далее. В появившемся поле Поместить диаграмму на листе выберем отдельном. Шаг 4 из 4. Сделать на графике необходимые пометки можно с помощью панели Рисование. (Рис. 8)
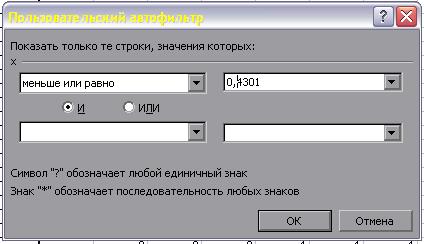
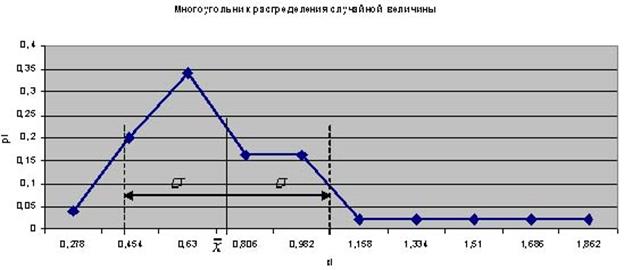
На рисунке 8 по оси абсцисс отложена величина посева на душу в десятинах в губерниях Европейской части России, а по оси ординат – pi, как относительная величина числа губерний, обладающих признаком x Указанные точки распределяют губернии на малоземельные или бедные ( Перейдём на Лист 1 и в соответствии с указанными интервалами определим перечни губерний, относящихся к категориям. Для этого в Excel предусмотрена функция Автофильтр. ▲ Применение функции Автофильтр. 1. Вычислим опорные точки интервалов. В ячейку E1 на Лист1 введём формулу: =Лист2!G12-Лист2!H12. Формула ссылается на Лист2 и вычисляет разницу 2. Выделим ячейки А1:С1 и выполнимкоманду Данные – Сортировка. Ячейки отметились символом Ø Нажмем его в ячейке С1 и выберем меню Условие. Это диалоговое окно позволяет осуществить отбор значений, попадающих в заданный интервал. В первом поле выберем меньше или равно. Во втором поле укажем значение из ячейки Е1 (рис. 9).
Рис. 9 Нажмем ОК и получим список значений, удовлетворяющий введенному условию:
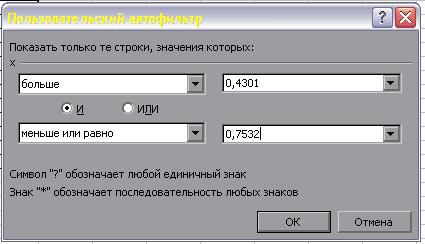
Скопируем этот список B2:B6 на Лист3 в ячейки А1:A6 (оставим первую строку для обозначения рядов) Ø В меню Автофильтр В первом поле выберем Больше, во втором введем значение из ячейки Е1. В третьем поле выберем меньше или равно, в четвертое поле значение из ячейки F1 (рис.10).
Рис. 10
Нажмем ОК и получим список значений, удовлетворяющий введенному условию:
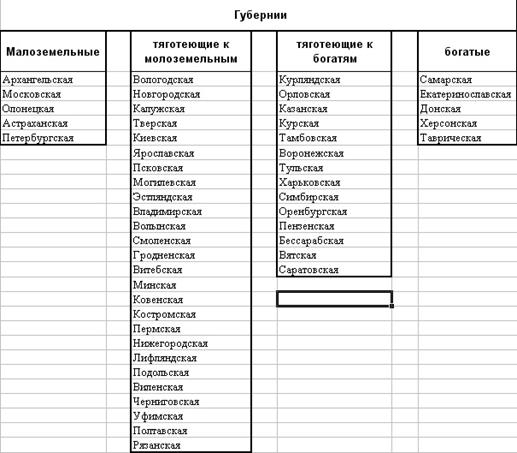
Скопируем этот список по столбцу В на Лист3 в ячейки С 2:С27 (оставим первую строку для обозначения рядов). Ø Аналогично применяя алгоритм для следующих двух интервалов и копируя полученный результат на Л ист3, мы получим следующие данные (столбцы названы в соответствии со смысловым значением интервала) (рис.11):
Рис. 11
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |

 x разобьем на десять интервалов и выберем ширину интервала d согласно следующей формулы:
x разобьем на десять интервалов и выберем ширину интервала d согласно следующей формулы: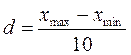
 , означающий число стоящее в середине i -го интервала, в ячейку Е1 - n
, означающий число стоящее в середине i -го интервала, в ячейку Е1 - n  , т.е. относительную величину ni.
, т.е. относительную величину ni.
 (при наведении курсор превращается в черный крестик) в нижнем правом углу выделения, «протащить» выделение до ячейки А11. Эта операция называется автозаполнение ячеек. В данном случае мы задали алгоритм простой последовательности чисел, указав ряд чисел 1, 2.
(при наведении курсор превращается в черный крестик) в нижнем правом углу выделения, «протащить» выделение до ячейки А11. Эта операция называется автозаполнение ячеек. В данном случае мы задали алгоритм простой последовательности чисел, указав ряд чисел 1, 2.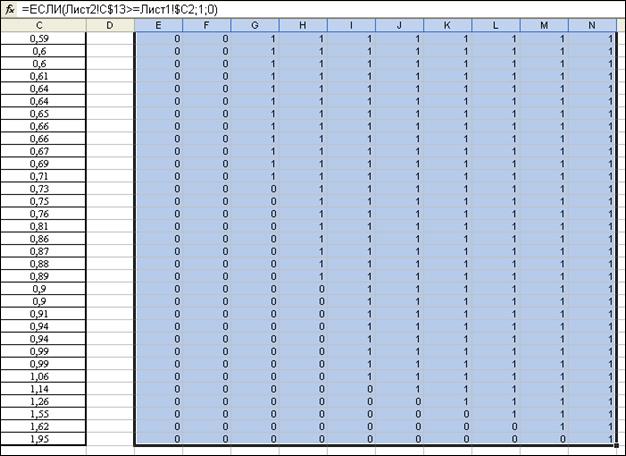
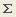 на панели инструментов. Автоматически по столбцу E посчитается сумма. Применим автозаполнение по строке до ячейки N51. В ячейку Е53 внесём формулу: =E52-D52. Применим автозаполнение до ячейки N53. Теперь эта строка содержит количество попавших в определённый интервал значений. (Рис.3)
на панели инструментов. Автоматически по столбцу E посчитается сумма. Применим автозаполнение по строке до ячейки N51. В ячейку Е53 внесём формулу: =E52-D52. Применим автозаполнение до ячейки N53. Теперь эта строка содержит количество попавших в определённый интервал значений. (Рис.3)


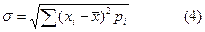
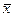 расположена посередине всего интервала изменения числовых значений x
расположена посередине всего интервала изменения числовых значений x 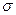 определяет меру рассеяния величин x
определяет меру рассеяния величин x 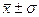 .
.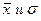
 на панели инструментов Стандартная, произойдет автоматическое суммирование по столбцу G. Получившийся результат – значение
на панели инструментов Стандартная, произойдет автоматическое суммирование по столбцу G. Получившийся результат – значение 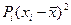 . В ячейку Н2 введём формулу: =F2*((D2-G$12)^2) в качестве реализации (4). Применим автозаполнение до ячейки H11.
. В ячейку Н2 введём формулу: =F2*((D2-G$12)^2) в качестве реализации (4). Применим автозаполнение до ячейки H11. на панели инструментов Стандартная.
на панели инструментов Стандартная.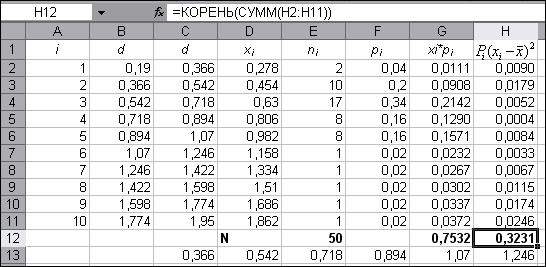
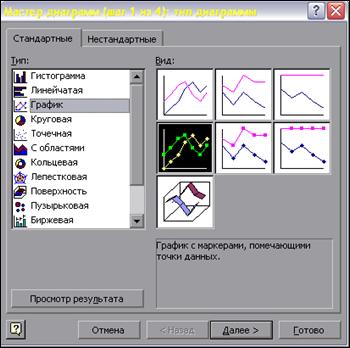 Рис.6
Рис.6
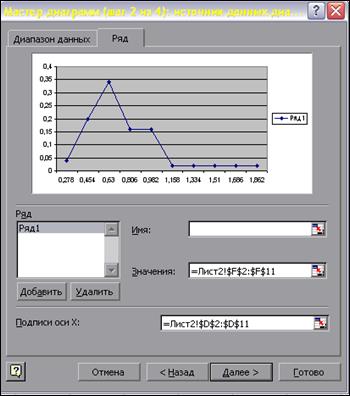 Рис.7
Рис.7
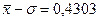 и
и 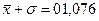 .
.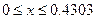 ), тяготеющие к бедным (
), тяготеющие к бедным (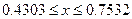 ),тяготеющие к богатым (
),тяготеющие к богатым (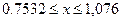 ) и многоземельные или богатые (
) и многоземельные или богатые (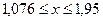 ).
).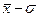 . Далее ячейка F1 содержит формулу =Лист2!G12 - прямая ссылка на значение
. Далее ячейка F1 содержит формулу =Лист2!G12 - прямая ссылка на значение 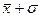 . Ячейка H1 содержит формулу =Лист2!C11. Таким образом, строка содержит опорные точки интервалов.
. Ячейка H1 содержит формулу =Лист2!C11. Таким образом, строка содержит опорные точки интервалов. - означает включенный режим автофильтрации.
- означает включенный режим автофильтрации.