Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Институт математики и информатикиСодержание книги
Поиск на нашем сайте
Правительство Москвы Московский департамент образования Государственное образовательное учреждение высшего профессионального образования Московский городской педагогический университет ИНСТИТУТ МАТЕМАТИКИ И ИНФОРМАТИКИ Кафедра естественнонаучных дисциплин
УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ДИСЦИПЛИНЫ
Дисциплина: Математика Направление подготовки: Психолого-педагогическое образование (Психология и педагогика дошкольного образования) (стандарт 0504б_зппдо) Степень(квалификация) бакалавр
Составитель: кандидат технических наук, доцент Селина В.О.
Москва 2012
Знания и умения выпускника определяются компетенциями:
Компетенция ОК-15 – Владеет методами количественного анализа и моделирования, теоретического и экспериментального исследования. Компетенция ОК-16 - Понимает роль и значение информации и информационных технологий в развитии современного общества и экономических знаний. Компетенция ОК-17 - Владеет основными методами, способами и средствами получения, хранения, переработки информации, имеет навыки работы с компьютером как средством управления информацией.
Стандарт дисциплины: аналитическая геометрия и линейная алгебра; дифференциальное и интегральное исчисления; дифференциальные уравнения; элементы теории вероятности; математическая статистика.
Программа курса:
I. Линейная алгебра Теория определителей: определители 2-го и 3-го порядков и правила их вычисления; определителя n-го порядка; свойства определителей, вычисление определителя разложением по элементам строки (столбца). Формулы Крамера для решения системы линейных алгебраических уравнений. Теорема Крамера о единственности решения системы линейных алгебраических уравнений. Матрицы: определение матрицы; ранг матрицы; элементарные преобразования матрицы; операции умножения и сложения матриц; единичная матрица; обратная матрица. Решение системы линейных алгебраических уравнений: теорема о числе решений, метод Гаусса, решение с помощью обратной матрицы.
II. Дифференциальное и интегральное исчисление.
Функция: определение, свойства и способы задания; производная, геометрический смысл производной, исследование функций с помощью первой и второй производной, дифференциал функций, инвариантность формы дифференциала. Интеграл: неопределенный интеграл как операция обратная дифференцированию, свойства неопределенного интеграла, приемы интегрирования; определенный интеграл и его вычисление, приложения определенного интеграла.
III. Дифференциальные уравнения и численные методы их решения Дифференциальные уравнения первого порядка. Типы дифференциальных уравнений и методы их решения. Линейные дифференциальные уравнения первого порядка. Дифференциальные уравнения n-го порядка. Задача Коши. Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и методы их решения. Численное интегрирование дифференциальных уравнений первого порядка методом Эйлера и Рунге-Коши. IV. Аналитическая геометрия
Компланарные векторы. Разложение вектора по трем некомпланарным векторам. Афинная система координат. Представление вектора в афинной системе координат. Переход от одной афинной системы координат к другой. Прямоугольная система координат в пространстве. Разложение вектора по ортам осей. Линейные операции над векторами в координатной форме. Деление отрезка в данном отношении. Скалярное произведение ортов. Векторное произведение координатных ортов. Векторно-скалярное произведение трех векторов. Полярная система координат на плоскости. Уравнение прямой линии. Общее уравнение прямой линии. Уравнение прямой в отрезках, проходящей через заданную точку в данном направлении. Угол между прямыми. Нормальное уравнение прямой. Расстояние от точки до прямой. Уравнение окружности как частный случай плоской линии. Параметрическое уравнение линии. Канонические координаты. Канонические уравнения параболы и эллипса. Параметры, определяющие эти кривые. Каноническое уравнение гиперболы. Плоскость и прямая в пространстве. Параметрическое и общее уравнение плоскости. Уравнение плоскости. Частные случаи уравнения плоскости. Взаимное расположение двух плоскостей. Прямая как пересечение двух плоскостей. Пучок плоскостей. Взаимное расположение двух прямых в пространстве. Два полупространства, определяемых данной плоскостью. Плоскость в прямоугольной системе координат. Нормальное уравнение плоскости. Расстояние от точки до плоскости. Угол между прямой и плоскостью. Угол между двумя плоскостями. Студент, не выполнивший необходимый минимум работ, до сессии не допускается. Приложение 1 Домашние задания Домашнее задание № 1. Определители.
Задача 1. Найти при каком значении параметра α определитель
Задача 2. Найти при каком значении α определитель
Задача 3. Найти при каком значении α определитель
Задача 4. Найти при каком значении α определитель
Задача 5. Найти при каком значении α определитель
Задача 6. Найти при каком значении α определитель
Задача 7. Найти при каком значении α определитель
Задача 8. Найти при каком значении α определитель
Задача 9. Найти значениеопределителя
Задача 10. Найти значение определителя
Задача 11. Найти значение определителя
Задача 12. Вычислить определитель
Задача 13. Вычислить определитель
Задача 14. Вычислить определитель
Задача 15. Вычислить определитель
Задача 16. Вычислить определитель
Задача 17. Вычислить определитель
Задача 18. Разложением по первой строке вычислить определитель
Задача 19. Разложением по первой строке вычислить определитель
Задача 20. Разложением по первой строке вычислить определитель
Задача 21. Разложением по первой строке вычислить определитель
Домашнее задание №2 Матрицы и операции над ними
Задача 1. Дана матрица
Найти сумму двух следующих ее элементов а11+ а32. Ответ: (- 7). Задача 2. Дана матрица найти сумму а12+ а23.
Ответ: (- 4). Задача 3. Найти сумму элементов, расположенных на главной диагонали.
Ответ: 15.
Задача 4. Найти сумму элементов, расположенных на второй диагонали.
Ответ: 9. Задача 5. Указать тип матрицы
Ответ: трапециевидная.
Задача 6. Указать тип матрицы
Ответ: единичная.
Задача 7. Указать тип матрицы
Ответ: верхняя.
Задача 8. Указать тип матрицы
Ответ: нижняя.
Задача 9. Указать тип матрицы
Ответ: симметричная.
Задача 10. Найти сумму двух следующих матриц
Ответ: Задача 11. Найти сумму двух следующих матриц
Ответ:
Задача 12. Найти сумму двух следующих матриц
Ответ:
Задача 13. Найти сумму двух следующих матриц
Ответ: Задача 14. Из матрицы А вычесть матрицу В:
Ответ:
Задача 15. Матрицу Ответ: λ• А=
Задача 16. Найти произведение А и В:
Ответ:
Задача 17. Найти произведение А и В:
Ответ: Задача 18. При каком значении параметра λ матрица
Ответ: λ = - 2
Задача 19. При каком значении параметра λ матрица
Задача 20. При каком значении параметра λ матрица
Задача 21. При каком значении параметра λ матрица
Задача 22. При каком значении параметра λ матрица
Задача 23. При каком значении параметра λ матрица
Ответ: λ = 2; Задача 24. Вычислить определители произведения матриц А и В
Ответ: Задача 25. Вычислить определители произведения матриц А и В
Ответ: Задача 26. Вычислить определители произведения матриц А и В
Ответ: Задача 27. Вычислить определители произведения матриц А и В
Ответ: Задача 28. Вычислить определители произведения матриц А и В
Ответ:
Задача 29. Найти ранг матрицы
Ответ: r = 1
Задача 30. Найти ранг матрицы
Ответ: r = 2
Задача 31. Найти ранг матрицы
Ответ: r = 2
Задача 32. Найти ранг матрицы
Ответ: r = 1
Задача 33. Найти ранг матрицы
Ответ: r = 2
Задача 34. При каком значении параметра λ матрица А не имеет обратной.
Ответ:
Задача 35. При каком значении параметра λ матрица А не имеет обратной.
Задача 36. При каком значении параметра λ матрица А не имеет обратной.
Задача 37. При каком значении параметра λ матрица А не имеет обратной.
Задача 38. При каком значении параметра λ матрица А не имеет обратной.
Задача 39. При каком значении параметра λ матрица А не имеет обратной.
Домашнее задание №3. Системы линейных алгебраических уравнений. Задача 1. Решить систему алгебраических уравнений
Задача 2. Решить систему алгебраических уравнений
Задача 3. Решить систему алгебраических уравнений
Задача 4. Решить систему алгебраических уравнений
Задача 5. Решить систему алгебраических уравнений
Задача 6. По заданным матрицам А и В восстановить вид системы линейных алгебраических уравнений:
Ответ: Задача 7. По заданным матрицам А и В восстановить вид системы линейных алгебраических уравнений:
Ответ: Задача 8. По заданным матрицам А и В восстановить вид системы линейных алгебраических уравнений:
Ответ: Задача 9. По заданным матрицам А и В восстановить вид системы линейных алгебраических уравнений:
Ответ: Задача 9. По заданным матрицам А и В восстановить вид системы линейных алгебраических уравнений:
Ответ:
Задача 10. По заданной системе линейных алгебраических уравнений третьего порядка восстановить вид матрицы системы:
Задача 11. По заданной системе линейных алгебраических уравнений третьего порядка восстановить вид матрицы системы:
Задача 12. По заданной системе линейных алгебраических уравнений третьего порядка восстановить вид матрицы системы:
Задача 13. По заданной системе линейных алгебраических уравнений третьего порядка восстановить вид матрицы системы:
Задача 14. По заданной системе линейных алгебраических уравнений третьего порядка восстановить вид матрицы системы:
Задача 15. Найти определители матриц следующих систем линейных алгебраических уравнений
Задача 16. Найти определители матриц следующих систем линейных алгебраических уравнений
Задача 17. Найти определители матриц следующих систем линейных алгебраических уравнений
Задача 18. Найти определители матриц следующих систем линейных алгебраических уравнений
Задача 19. Найти определители матриц следующих систем линейных алгебраических уравнений
Задача 20. Представить в матричном виде системы линейных алгебраических уравнений
Ответ: Задача 21. Представить в матричном виде системы линейных алгебраических уравнений
Ответ: Задача 22. Представить в матричном виде системы линейных алгебраических уравнений
Ответ:
Задача 23. Представить в матричном виде системы линейных алгебраических уравнений
Ответ:
Задача 24. Представить в матричном виде системы линейных алгебраических уравнений
Ответ: Домашнее задание №4 Область определения. Частные производные. Производная по направлению. Градиент. Дифференциал.
Задача 1. Найти область определения функции 2-ух переменных
Ответ: I и III квадранты без границ. Задача 2. Найти область определения функции
Ответ: Вся плоскость, за исключением точек окружности Задача 3. Найти область определения функции
Ответ: I и III квадранты. Частные производные. Задача 1. Вычислить
Ответ: Задача 2. Вычислить
Ответ: Задача 3. Вычислить
Ответ: Производная по направлению. Задача 1. Вычислить производную функции
В точке Ответ: 7. Задача 2. Вычислить производную функции
В точке Ответ: Градиент. Задача 1. Найти градиент функции
Ответ: Задача 2. Найти градиент функции
Ответ: Задача 3. Найти градиент функции
Ответ: Дифференциал. Задача 1. Найти дифференциалы следующих функций 1) Ответ: 2) Ответ: 3) Ответ: Задача 2. Вычислить приближенное значениечислового выражения Домашнее задание №5. Производные и экстремумы функций.
Приложение 2 Лабораторные работы Семестр I
Рис. 15.3 Рис. 15.4 Легко видеть, что при х=0,7 функция отрицательна, а при х=0,8 – положительна. 15. Повторим действия 6 – 10, заменяя в ячейке А2 число 0 на число 0,7, а в ячейке А3 изменив в формуле 1/10 на 1/100. Легко видеть, что при х=0,73 функция отрицательна, а при х=0,74 – положительна. 16. Еще раз повторим действия 6 – 10, заменяя в ячейке А2 число 0,7 на число 0,73, а в ячейке А3 изменив в формуле 1/100 на 1/1000. Получим таблицу значений (см. рис. 15.4). Значение Таблица 1
Требуется составить наиболее дешёвый рацион, при котором каждое животное получило бы необходимые количества питательных веществ А, В и С. Решение. Пусть х1, х2, х3 – количества кормов I, II, III видов, включаемые в ежедневный рацион (х i ³0, i =1, 2, 3). Тогда должно быть:
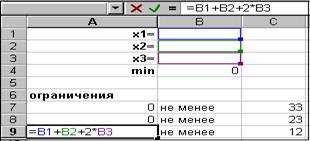
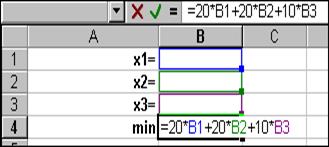
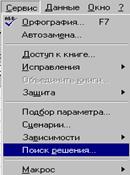
При этом линейная функция (стоимость рациона) f =20х1+20х2+10х3®min. (2) При решении задачи с помощью надстройки Поиск решения необходимо: 1. Открыть окно Microsoft Excel; 2. сделаем первый столбец А – столбцом заголовка, т.е. заполним ячейки A1¸А4 таблицы обозначениями х1, х2, х3 и min соответственно; 3. активизируйте ячейку В4 и запишите в неё формулу (2), см. рис. 16.1; 4. в область ячеек А7¸С9 запишите систему (1), см. рис. 16.2;
Рис. 16.1 Рис. 16.2 5. для решения поставленной задачи в меню Сервис выполните нажатие ЛКМ на Поиск решения…; 6.
7. У нас осталось незаполненным поле «Ограничения», поэтому ЛКМ нажмем на копке Добавить; 8. после того, как появилось окно Добавление ограничения активизируйте поле «Ссылка на ячейку» и выполните нажатие ЛКМ на ячейке А7. В следующем поле выберите знак «>=», затем в поле «Ограничения» выполните нажатие ЛКМ на ячейке С7 (см. рис. 16.4);
9. аналогично описанному в предыдущем пункте добавьте ограничения, записанные в область ячеек А8¸С9; 10. помимо ограничений, введённых нами в электронную таблицу, в задаче есть ещё одно ограничение, которое мы тоже должны внести (х i ³0). Поэтому мы должны добавить ещё одно ограничение: $B$1:$B$3>=0. 11. Теперь все ограничения нами учтены и мы можем нажать лкм на ОК, после чего мы снова попадаем в диалоговое окно Поиск решения, где лкм нажимаем на Выполнить. 12. Появляется диалоговое окно Результаты поиска решения, в котором компьютер предлагает по умолчанию сохранить найденное решение. Если вы согласны с полученными результатами, то лкм нажмите на кнопке ОК. Результат полученных вычислений представлен на рис. 16.5.
Рис. 16.5 Задача 2. На товарных станциях С 1 и С 2 имеется по 30 комплектов мебели. Известно, что перевозка одного комплекта со станции С 1 в магазины М1, М2, М3 стоит 1р., 3р., 5р., а стоимость перевозки со станции С 1 в те же магазины – 2р., 5р., 4р. необходимо доставить в каждый магазин по 20 комплектов мебели. Составить план перевозок так, чтобы затраты на транспортировку мебели были наименьшими. Решение. Количество комплектов мебели, перевозимых со станции С 1 в магазины М1, М2, М3 обозначим через х1, х2, х3, а со станции С 2 – через х4, х5, х6. Тогда схема перевозок буде выглядеть следующим образом: Таблица 2
В соответствии с условием задачи х i ³0 (i =1, 2, …, 6). Задача сводится к тому, чтобы найти такое неотрицательное решение системы (3)
при котором линейная функция (стоимость перевозок)
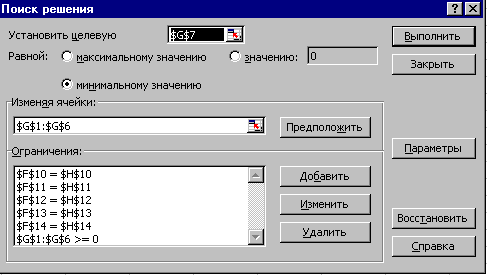
имеет наименьшее значение. Далее приступим к решению задачи в программе Microsoft Excel. Для этого: 13. сделайте столбец F – столбцом заголовка, т.е. заполните ячейки F1¸ F7 таблицы обозначениями х1, х2, х3 х4, х5, х6 и min соответственно; 14. выполните действия, аналогичные действиям, описанным в пунктах 3–11, меняя только ссылки на ячейки, в результате чего окно Поиск решения будет выглядеть так как представлено на рис. 16.6, а решение задачи – на рис. 16.7.
Рис. 16.6
Рис. 16.7
Задания для самостоятельной работы. Задача №1. Для участия в командных соревнованиях по лёгкой атлетике спортклуб должен выставить команду, состоящую из спортсменов I и II разрядов. Соревнования проводятся по бегу, прыжкам в высоту и прыжкам в длину. В беге должны участвовать 5 спортсменов, в прыжках в длину – 8 спортсменов, в прыжках в высоту – не более 10. Количество очков, гарантируемое спортсмену каждого разряда по каждому виду, указано в таблице:
Распределить спортсменов команды так, чтобы сумма очков команды была наибольшей, если известно, что в команде I разряд имеют только 10 спортсменов. Задача №2. Три завода производят одно и то же изделие, которое отправляется четырем потребителям. Известно, что I завод поставляет 90 вагонов изделий, II – 30 вагонов, III – 40 вагонов. Для потребителей требуется: первому – 70 вагонов, второму – 30, третьему – 20 и четвёртому – 40. Стоимость (в руб.) перевозки одного вагона между каждым поставщиком и потребителем указаны в следующей таблице:
Определить минимальный по стоимости план перевозок.
Задача №3. Груз, хранящийся на складах, в каждом соответственно 60, 80 и 106 машин, требуется перевезти в четыре магазина. В первый магазин требуется 44 машины, во второй – 70, в третий – 50, в четвёртый – 82. Стоимость прогона одной машины за 1 км составляет 10 коп. расстояния между складами и магазинами указаны в таблице:
Составить оптимальный по стоимости план перевозки груза из складов в магазины.
Семестр II Задания 1. Для последовательности 1) перейдите на новый лист. Для этого поместите указатель мыши на ярлычок листа, с которым вы будете работать (Лист2) и щелкните мышью на нем. Если новых листов больше нет, то вставьте его, выбрав команду Вставка → Лист. После этого добавится новый лист со следующим порядковым номером. Оставьте активной ячейку А1. 2) выберите команду Сервис → Макрос → Макросы, затем в окне диалога Макросы подтвердите выбор Макроса1 и щелкнитена кнопке Выполнить; 3) в ячейку А1 дополнительно введите 4)в ячейку В5 введите формулу первого члена последовательности:=(A5^3-A5-3)/(2*A5^2+A5+1);
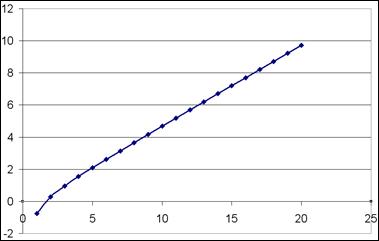
5) выполните последовательно оставшиеся пункты. В качестве ответа вы должны получить график функции f(n). Ответ: 2. Для последовательности
Ответ: 3. Для последовательности
Ответ:
|

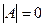
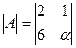 Ответ: α=3.
Ответ: α=3.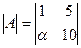 Ответ: α = 2;
Ответ: α = 2;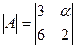 Ответ: α = 1;
Ответ: α = 1;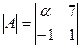 Ответ: α = - 7;
Ответ: α = - 7;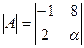 Ответ: α = -16;
Ответ: α = -16;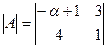 Ответ: α = - 11;
Ответ: α = - 11;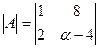 Ответ: α = 20;
Ответ: α = 20;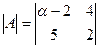 Ответ: α = 12
Ответ: α = 12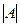 :
: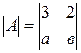 Ответ:
Ответ: 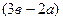
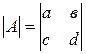 , Ответ:
, Ответ: 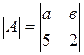 , Ответ:
, Ответ: 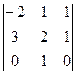 , Ответ:
, Ответ: 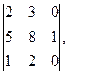 Ответ:
Ответ: 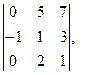 Ответ:
Ответ: 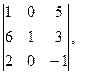 Ответ:
Ответ: 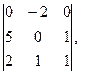 Ответ:
Ответ: 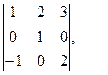 Ответ:
Ответ: 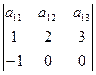 Ответ:
Ответ: 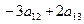
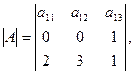 Ответ:
Ответ: 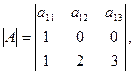 Ответ:
Ответ: 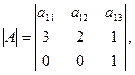 Ответ:
Ответ: 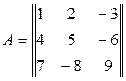
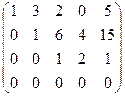
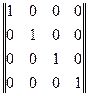
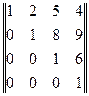
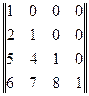
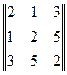

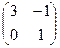
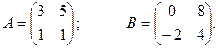
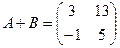 ;
;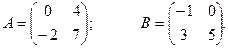
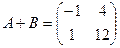 ;
;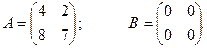
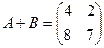
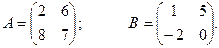
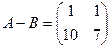 ;
;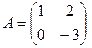 умножить на число λ=2.
умножить на число λ=2.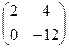 ;
;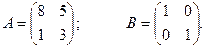
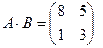 ;
;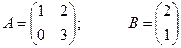
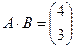
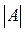 является вырожденной.
является вырожденной.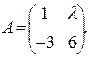
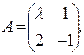 . Ответ: λ= -2;
. Ответ: λ= -2;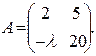 . Ответ: λ= - 8;
. Ответ: λ= - 8;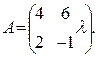 . Ответ: λ= 3;
. Ответ: λ= 3;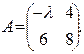 . Ответ: λ= - 3;
. Ответ: λ= - 3;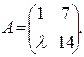 .
.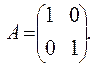 ,
, 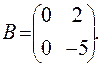 ,
,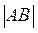 =0;
=0;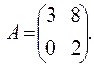 ,
, 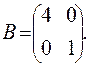 ,
,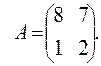 ,
, 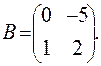 ,
,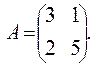 ,
, 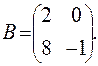 ,
,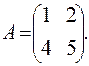 ,
, 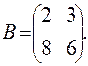 ,
,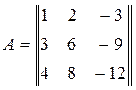
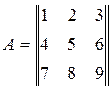
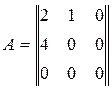
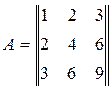
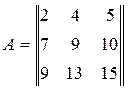
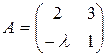
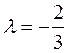
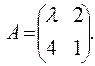 ,, Ответ:
,, Ответ: 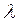 = 8;
= 8;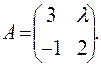 ,, Ответ:
,, Ответ: 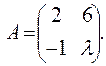 ,, Ответ:
,, Ответ: 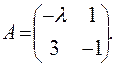 ,, Ответ:
,, Ответ: 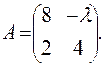 , Ответ:
, Ответ: 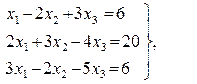 Ответ: х1 = 8, х2 = 4, х3 = 2;
Ответ: х1 = 8, х2 = 4, х3 = 2;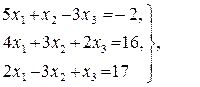 Ответ: х1 = 3, х2 = - 2, х3 = 5;
Ответ: х1 = 3, х2 = - 2, х3 = 5;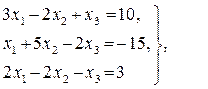 Ответ: х1 = 1, х2 = - 2, х3 = 3;
Ответ: х1 = 1, х2 = - 2, х3 = 3;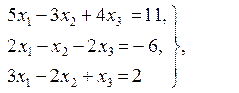 Ответ: х1 = 1, х2 = 2, х3 = 3;
Ответ: х1 = 1, х2 = 2, х3 = 3;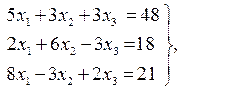 Ответ: х1 = 3, х2 = 5, х3 = 6
Ответ: х1 = 3, х2 = 5, х3 = 6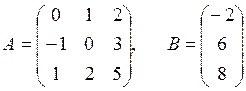
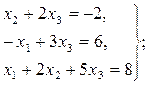
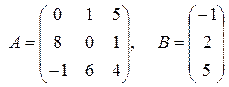
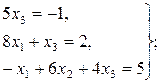
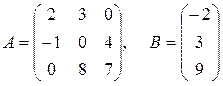
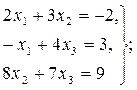
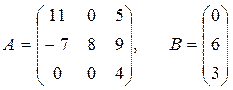
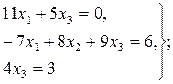
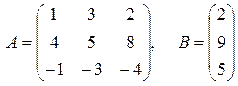
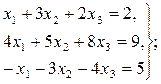

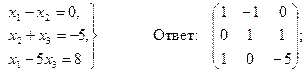

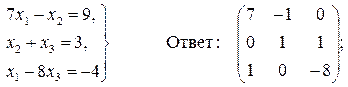
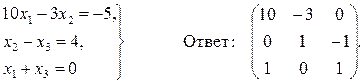
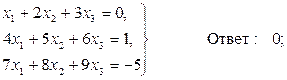
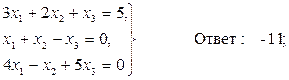
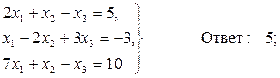
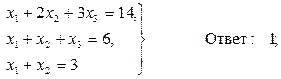
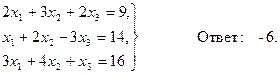
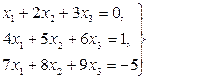
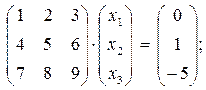
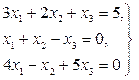
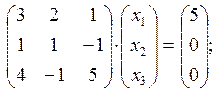
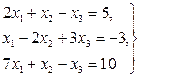
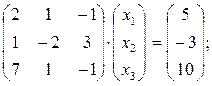
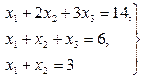
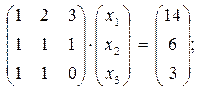
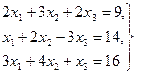

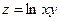
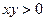
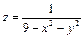
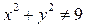
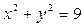
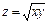
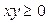
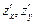
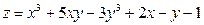
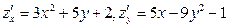
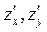
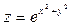
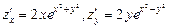
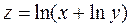
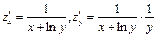
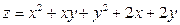
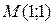 по направлению вектора
по направлению вектора 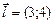
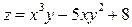
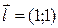
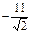
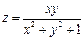 в точке
в точке 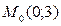
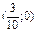
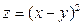 в точке
в точке 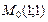
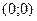
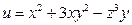 в точке
в точке 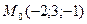
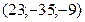
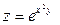
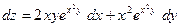
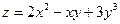
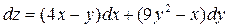
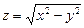
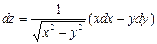
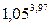 с помощью полного дифференциала 1-го порядка функции двух переменных
с помощью полного дифференциала 1-го порядка функции двух переменных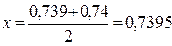 можно считать корнем уравнения с точностью до 0,0005.
можно считать корнем уравнения с точностью до 0,0005.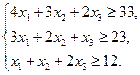 (1)
(1)
 в появившемся окне в поле «Установить целевую» нажатием ЛКМ выделите ячейку В4; в поле «Изменяя ячейки»выделите область В1¸В3; нажатием ЛКМ установите флажок в поле «минимальному значению» (см. рис. 16.3).
в появившемся окне в поле «Установить целевую» нажатием ЛКМ выделите ячейку В4; в поле «Изменяя ячейки»выделите область В1¸В3; нажатием ЛКМ установите флажок в поле «минимальному значению» (см. рис. 16.3).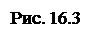

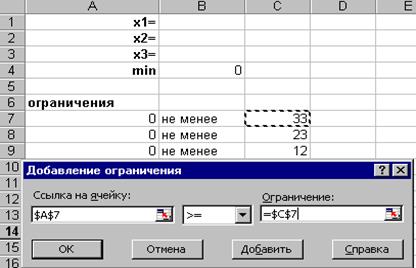 Рис. 16.4
Рис. 16.4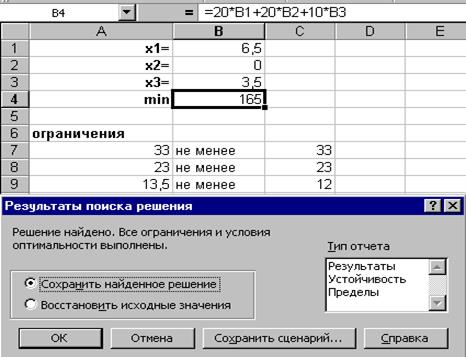
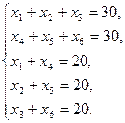 (3)
(3)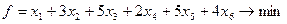 (4)
(4)
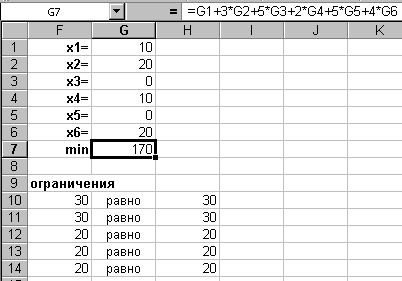
 Потребители
Поставщики
Потребители
Поставщики
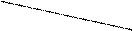 Магазины
Склады
Магазины
Склады
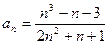 создайте таблицу и постройте график, по аналогии с примером, описанным выше, пользуясь при этом записанным Макросом1 на новом Листе2. С этой целью выполните следующие действия:
создайте таблицу и постройте график, по аналогии с примером, описанным выше, пользуясь при этом записанным Макросом1 на новом Листе2. С этой целью выполните следующие действия: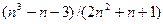 .
.
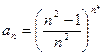 создайте таблицу и постройте график.
создайте таблицу и постройте график.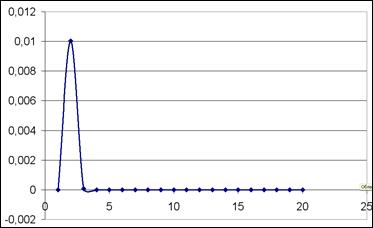
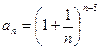 создайте таблицу и постройте график.
создайте таблицу и постройте график.