
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрица. Линейные операции с матрицами. Умножение матриц, обратная матрица.Содержание книги
Поиск на нашем сайте
Матрица – таблица чисел, состоящая из m строк и n столбцов Под линейными операциями над матрицами понимают: сложение матриц, умножение матриц на любое действительное число. Для данных операций справедливо 8 аксиом: 1) A+B=B+A 2) A+(B+C)=(A+B)+C 3) A+θ=A 4) A+(-A)= θ 5) 1*A=A 6) 7) α(A+B)=αA+Αb 8) (α+β)A=αA+Βa Умножение матриц. Для перемножения матриц необходимо чтобы кол-во столбцов у 1й матрицы = кол-ву строк у 2й матрицы. Матрица-строка умножается на матрицу столбец. Свойства умножения матриц: 1)A*B≠B*A 2) A*E(1я матрица)=E*A=A 3)A*(BC)=(AB)*C 4) A*(B+C)=AB+AC 5) (A+B)*C=AC+BC (матрицы умножаются строго по порядку) Обратные матрицы. Обр. матр. Называется вырожденной, если ее определитель равен 0, в противном случае невырожденной. Если С=AB и определитель С=0, то матрица С-вырожденная и хотя бы одна из А и B тоже вырожденная. B – обратная матрица к А, если справедливо равенство AB=BA=E и обозначается 2)
6. Элемнтарные преобразования матриц. Приведение к ступенчатому виду. Эл. Преобразования: 1) перестановка местами любых 2х строк или столбцов матрицы. 2) Умножение любой строки или столбца на любое действ. Число не равное 0. В результате преобразований получается новая матрица эквивалентная данной, причем их определители равны. Метод гаусса, ранг матрицы. Матрица А порядка MxN называется ступенчатой, если для любых Аij=0 при i>j, для любых i>r, для любых Aii≠0 при i≤r и r≥1, r≤min(m,n) Amxn=
7. Пространство Множество элементов x,y,z…. 1) X+Y=Z 1) Множество действ чисел 2) множество геометрических векторов 3) множество матриц одного порядка 4) множество многочленов какой-либо степени и т.д. N-мерным арифметическим вектором называется упорядоченная совокупность n-чисел(действит) и записывается Рассмотрим линейное пространство L для него справедливы 8 аксиом, удовлетворяющие введенным в пространстве L операций сложения элементов и умножения элементов на число. 1) x+y=y+x 2) x+(y+z)=(x+y)+z 3) x+θ=x 4)
8. Линейная зависимость. Базис. Линейное пространство в Линейно зависимые и линейно независимые системы векторов. Опр. Система векторов (e1,e2,…ek) Теорема необходимое и достаточное условие линейной зависимости системы векторов. Для того, чтобы система векторов (e1,e2,…ek)
Свойства линейно зависимых и линейно независимых систем векторов: 1) Любая система содержащая Базис линейного пространства. Опред. Линейное пространство L называется n-мерным, если в нем существует линейно-независимые системы n векторов, а любая система состоящая из n+1 вектора линейно зависимая. В этом случае число n называется размерностью линейного пространства L и обозначается dimL=n или Теорема в n мерном пространстве L существует базис из n векторов. Без док-ва. Рассмотрим арифметическое пространство Теорема о единственности разложения вектора по базису. Если система векторов e1,e2,…,en образует базис в пространстве
Подпространство линейного пространства
|
|||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 209; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.103.151 (0.008 с.) |


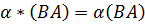
 . Теорема о существовании обратной матрицы. Если матрица А невырожденная, то у нее существует обратная матрица, которая находится по формуле
. Теорема о существовании обратной матрицы. Если матрица А невырожденная, то у нее существует обратная матрица, которая находится по формуле  Матрица
Матрица 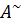 получается из матрицы А заменой каждого элемента матрицы А его алгебраическим дополнением. Теорема о единственности обратной матрицы. Если матрица обратима, то у нее существует только 1 обратная матрица. Док-во: предоложим, что у матрицы А есть 2 обратных матрицы B,C. Тогда т.к. B – обратная к А, следовательно AB=BA=E, но с другой стороны AC=CA=E Рассмотрим матрицу B=BE по 5 свойству умножения матриц B=BE=B(AC)=(BA)C=EC=C,что противоречит свойству, следовательно B=C. Свойства обратных матриц: 1)
получается из матрицы А заменой каждого элемента матрицы А его алгебраическим дополнением. Теорема о единственности обратной матрицы. Если матрица обратима, то у нее существует только 1 обратная матрица. Док-во: предоложим, что у матрицы А есть 2 обратных матрицы B,C. Тогда т.к. B – обратная к А, следовательно AB=BA=E, но с другой стороны AC=CA=E Рассмотрим матрицу B=BE по 5 свойству умножения матриц B=BE=B(AC)=(BA)C=EC=C,что противоречит свойству, следовательно B=C. Свойства обратных матриц: 1)  Док-во:
Док-во:  Докажем, что
Докажем, что  *
*  ‑ обратная к (AB) (AB)(
‑ обратная к (AB) (AB)( )=A(B
)=A(B  )
)  =AE
=AE  =E(
=E( )(AB)=
)(AB)=  3) |
3) | 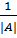 4) определитель транспонированной матрицы
4) определитель транспонированной матрицы  |(
|( )|=
)|= 
 rg=1 Любую прямоугольную матрицу можно привести к ступенчатому виду с помощью элементарных преобразований путем перестановки любых 2х строк, умножения любой строки на число или сложения любых 2х строк. Способ приведения любой прямоугольной матрицы к ступенчатой форме-метод Гаусса.
rg=1 Любую прямоугольную матрицу можно привести к ступенчатому виду с помощью элементарных преобразований путем перестановки любых 2х строк, умножения любой строки на число или сложения любых 2х строк. Способ приведения любой прямоугольной матрицы к ступенчатой форме-метод Гаусса.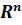 арифметических векторов (линейное пространство).
арифметических векторов (линейное пространство). L называется линейным пространством, если для любых элементов x и y из L и для любых α
L называется линейным пространством, если для любых элементов x и y из L и для любых α  =(x1,x2,…,xn)
=(x1,x2,…,xn)  Для арифметических векторов справедливы операции сложения векторов и умножение вектора на число и аналогичные операции с векторами. Геометрические векторы можно рассматривать, как трехмерные арифметические вектора, а пространство геометрических векторов можно рассматривать, как пространство 3х мерных арифметических векторов.
Для арифметических векторов справедливы операции сложения векторов и умножение вектора на число и аналогичные операции с векторами. Геометрические векторы можно рассматривать, как трехмерные арифметические вектора, а пространство геометрических векторов можно рассматривать, как пространство 3х мерных арифметических векторов.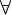 x
x 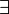 (-x)
(-x)  7)
7)  Элементы линейного пространства принято называть векторами. Пространство- векторное линейное пространство.
Элементы линейного пространства принято называть векторами. Пространство- векторное линейное пространство. Достаточность: Пусть 1 из векоров системы можно представить в виде лин. Комбинации остальных векторов системы. Тогда докажем, что система линейно зависимая. Пусть для определения ek является линейной комбинацией остальных векторов системы. Тогда для него найдутся числа
Достаточность: Пусть 1 из векоров системы можно представить в виде лин. Комбинации остальных векторов системы. Тогда докажем, что система линейно зависимая. Пусть для определения ek является линейной комбинацией остальных векторов системы. Тогда для него найдутся числа  ek=
ek= 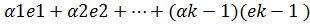
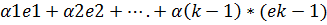 + (‑ 1)*ek=
+ (‑ 1)*ek= 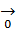 А значит αk=-1≠0 А это значит, что не все α1, α2, αk равны 0. Это значит что система линейно зависимая ч.т.д.
А значит αk=-1≠0 А это значит, что не все α1, α2, αk равны 0. Это значит что система линейно зависимая ч.т.д. . Базисом линейного пространства L называется любая система из n линейно-независимых векторов пространства L, причем любой вектор x принадлежащий пространству L может быть представлен в виде линейной комбинации базисных векторов, т.е. если система векторов (e1,e2,…,en) из L образует базис пространства L, то любой вектор x из L можно представить в виде
. Базисом линейного пространства L называется любая система из n линейно-независимых векторов пространства L, причем любой вектор x принадлежащий пространству L может быть представлен в виде линейной комбинации базисных векторов, т.е. если система векторов (e1,e2,…,en) из L образует базис пространства L, то любой вектор x из L можно представить в виде 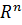 e1(1,0,0,…,0) e2 (0,1,0,…0) e3 (0,0,1,..,0) en (0,0,0,…,0,1) Данная система линейно независимая, т.к. чтобы α1e1+ α2e2+ α3e3=0 равенство выполнялось каждое α должно быть равно 0. Причем любой вектор x принадлежащий пространству
e1(1,0,0,…,0) e2 (0,1,0,…0) e3 (0,0,1,..,0) en (0,0,0,…,0,1) Данная система линейно независимая, т.к. чтобы α1e1+ α2e2+ α3e3=0 равенство выполнялось каждое α должно быть равно 0. Причем любой вектор x принадлежащий пространству  Множество L элементов из
Множество L элементов из 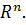 Пример. Рассмотрим множество L, арифметических векторов пространства
Пример. Рассмотрим множество L, арифметических векторов пространства 



