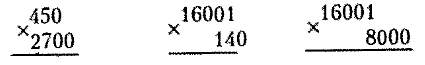Внетабличное умножение и деление

Случаи внетабличного умножения и деления изучаются в следующем порядке. Сначала рассматриваются правила умножения числа на сумму и суммы на число. Затем изучается умножение и деление чисел, оканчивающихся нулем, вводится умножение двузначного числа на однозначное и умножение однозначного числа на двузначное. Далее вводится правило деления суммы на число, на основе которого раскрывается прием деления двузначного числа на однозначное. Наконец, рассматривается деление двузначного числа на двузначное. При изучении этой темы вводится проверка умножения и деления.

Деление с остатком. Работа над делением с остатком в пределах 100 расширяет знания учащихся о действии деления, создает новые условия для применения знаний табличных результатов умножения и деления, для применения вычислительных приемов внетабличного умножения и деления, а также своевременно готовит учащихся к изучению письменных приемов деления.

Особенностью деления с остатком по сравнению с известными детям действиями является тот факт, что здесь по двум данным числам — делимому и делителю - находят два числа: частное и остаток.

Поэтому при изучении деления с остатком важно опираться на этот опыт детей и вместе с тем обогатить его. Полезно начать работу с решения жизненно практических задач. Например: «15 тетрадей раздай ученикам, по 2 тетради каждому. Сколько учеников получили тетради и сколько тетрадей осталось?»

Затем раскрывается соотношение между делителем и остатком: если при делении получается остаток, то он всегда меньше делителя.

В III и IV классах необходимо как можно больше включать разнообразных упражнений на все изученные случаи умножения и деления.

Письменное умножение и деление:

Большие числа удобно перемножать и делить письменно в столбик. Письменное умножение — это поразрядное умножение. Каждый разряд второго множителя умножается на первый множитель как одноразрядное число. В произведении поэтапного (разрядного) умножения первый разряд попадает в столбец того разряда второго множителя, на который умножают.

Правило. При умножении в столбик два множителя располагаются один под другим так, чтобы разряды чисел совпадали (находились в одном столбце). Слева ставится знак «х».

Если один из множителей или оба множителя оканчиваются нулями, то числа записываются так, чтобы значащие цифры наименьшего из разрядов находились в одном столбце. Нули переносятся в произведение и в поле записи поэтапных произведений не заносятся.

Поэтапные (разрядные) произведения складываются по разрядам и под чертой записывается результат. Слева от слагаемых произведений ставится знак «+».

Письменное умножение в столбик равноценно письменному умножению по разрядам в строку. При письменном умножении в строку применяются сочетательный и распределительный законы умножения (сумму заменяем слагаемыми и первый множитель умножаем на каждое из слагаемых).

Пример.
1 014 * 258 = 261 612
1 014 * 258 = 1 014 * (200 + 50 + 8) = 1 014 * 200 + 1 014 * 50 + 1014 * 8 = 202 800 + 50 700 + 8 112 = 261 612

Чтобы перемножить в столбик числа, оканчивающиеся нулями, нужно их подписать друг под другом так, чтобы первая справа значащая цифра первого множителя стояла под первой справа значащей цифрой второго множителя

.

Например: 1 014 * 258 = 261 612

· 1014 — первый множитель

· Х

· 258 — второй множитель

· --------- поэтапные произведения:

· 8112 — слагаемое (первое произведение)

· + 5070 — слагаемое (второе произведение)

· 2028 — слагаемое (третье произведение)

· ---------

· 261612 — сумма (результат умножения)

Примеры записи умножении чисел, оканчивающихся нулями.

· 450

· Х

· 270

· ---------

· 315 (45 * 7 = 315)

· +

· 90 (45 * 2 = 90)

· ---------

· 121500

Внимание! Нули в конце множителей в поэтапном умножении не принимают участия, а сразу все нули множителей переносятся в результат вычислений.

Правильная запись:

 

Неправильная запись

Письменное деление многозначных натуральных чисел осуществляется и в строку, и в столбик по этапам.

Правило. При письменном делении двух натуральных чисел слева записывается делимое, а справа от него через вертикальную черту — делитель.

Под делимым в столбец записываются поэтапные произведения каждого разряда частного на делитель. После каждого поэтапного произведения проводим горизонтальную черту, под которой записывается разность делимого и произведения, которая должна быть всегда меньше делителя, если разряд частного вычислен верно. Дополнив разность следующим разрядом делимого, принимаем это число за следующее поэтапное делимое.

Деление по этапам производим до первого разряда заданного условием делимого. Если последняя разность 0 или число, меньшее делителя, то деление натуральных чисел окончено.

Частное по разрядам (от большего к меньшему) записывается под горизонтальной чертой под делителем. В частном должно быть столько же разрядов, сколько этапов деления.

Рассмотрим пример: 12 546: 82
Производим деление первого этапа. Множитель (1) записываем как высший разряд частного. Вычисляем разность делимого и произведения первого этапа деления (125 — 82 = 43) и дописываем к ней справа один разряд из делимого, который стоит после наименьшего разряда числа, взятого для первого этана деления. Полученное число (434) служит делимым второго этапа
деления.

Делимое второго этапа делим на делитель (434: 82), определяем следующий разряд в частном (5) и остаток после второго этапа деления (24). Дописываем к остатку следующий разряд делимого и выполняем третий этап деления (246: 82). Определяем третье число в частном (3) и остаток (0).

Деление окончено после третьего этапа, следовательно, в частном — трех разрядное число (153).

Проще такое деление производить в столбик также в три этана (деление углом — это тоже поэтапное деление):

Делимое кратно 82, так как разделилось без остатка.

Основное свойство частного

Правило. Если делимое и делитель умножить или разделить на одно и то же натуральное число, то их частное не изменится.

Например:
12: 4 = 3

умножим делимое и делитель на 5, получим:
60: 20 = 3

Например:
625: 125 = 5
разделим делимое и делитель на 25, получим:
125: 5 = 5