Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 15. Теоремы сложения и умножения вероятностей. Формула полной вероятности и формула БайесаСтр 1 из 21Следующая ⇒
Операции над случайными событиями. Алгебра событий. Понятие совместности событий. Полная группа событий. Зависимость и независимость случайных событий. Условная вероятность события. Теорема сложения вероятностей для совместных и несовместных событий. Теорема умножения вероятностей зависимых и независимых событий. Полная группа событий. Понятие гипотезы. Априорные и апостериорные вероятности событий. Формула полной вероятности. Формула Байеса.
Тема 16. Повторение опытов. Поток событий Последовательность независимых испытаний. Формула Бернулли. Асимптотическая формула Пуассона и условия ее применения. Локальная теорема Муавра–Лапласа. Свойства функции
Тема 17. Случайные величины Понятие дискретной случайной величины. Закон распределения случайной величины. Функция распределения, ее свойства. Арифметические операции над случайными величинами. Числовые характеристики случайной величины. Понятие непрерывной случайной величины. Функция распределения, плотность распределения, их взаимосвязь и свойства. Числовые характеристики непрерывной случайной величины. Виды распределений. Нормальный закон распределения.
Тема 18. Системы случайных величин. Закон больших чисел. Случайные векторы. Закон распределения. Условные распределения случайных величин. Числовые характеристики случайных векторов. Условные математические ожидания. Функции регрессии. Ковариационная матрица. Коэффициенты корреляции. Функции случайных векторов и случайных величин, их законы распределения. Понятие о различных формах закона больших чисел. Леммы (неравенства) Чебышева и Маркова. Теоремы Бернулли и Чебышева. Центральная предельная теорема Ляпунова. Значение закона больших чисел для математической статистики.
Тема 19. Основные понятия математической статистики. Оценка функции распределения и параметров закона распределения Основы статистического описания. Гистограмма и полигон частот. кумулятивная кривая. Эмпирическое распределение и его свойства. Точечные оценки. Понятие статистики и достаточной статистики. Оценки наибольшего правдоподобия и их свойства. Интервальные оценки. Доверительные интервалы и области. Интервальные оценки параметров нормального, биномиального и пуассоновского распределений. Критерий Стьюдента и доверительные пределы для разности средних значений в двух нормальных выборках.
Тема 20. Проверка статистических гипотез Статистическая проверка гипотез. Критерии значимости, основанные на интервальных оценках (связь между уровнем значимости и коэффициентом доверия). Критерий и его связь с распределением. Применение критерия в случае распределения, зависящего от известных параметров. Примеры применения критерия. Общее понятие о статистической проверке гипотез. Простые и сложные гипотезы. Критерий и критическая область. Ошибки первого и второго рода. Гипотезы о математическом ожидании и дисперсии нормально распределенной случайной величины. Критерий Пирсона для проверки гипотезы о законе распределения. 1.4.3. Тематические планы изучения дисциплины
Очная форма обучения Срок обучения 5 лет
Заочная форма обучения Срок обучения 6 лет
Заочная форма обучения Срок обучения 3 года 6 месяцев
Примерный перечень вопросов к зачетам и экзаменам I. Математический анализ
1. Понятие функции. Общие свойства функций. Понятие обратной функции. 2. Определение числовой последовательности. Ограниченные и монотонные числовые последовательности. 3. Определение предела последовательности. 4. Основные теоремы о пределах последовательностей. Предельный переход в неравенствах. 5. Определение предела функции. Предел функции в точке и на бесконечности. Односторонние пределы. 6. Бесконечно малые и бесконечно большие функции и их свойства. 7. Теоремы о пределе функций. 8. Первый и второй замечательные пределы функций. 9. Сравнение бесконечно малых функций. 10. Понятие непрерывной функции. Непрерывность функции в точке и на множестве. 11. Точки разрыва функции и их классификация. Основные свойства непрерывных функций. 12. Понятие производной функции. Определение односторонних производных.
13. Геометрический и физический смысл производной. Уравнение касательной и нормали к функции в точке. 14. Общие правила дифференцирования и вычисления производной функции. 15. Связь между понятиями дифференцируемость и непрерывность функций. 16. Вычисление производной сложной функции. Производная обратной функции. Производная неявной функции. 17. Понятие эластичности функции. Общие свойства эластичности функции. 18. Понятие дифференциала функции и его геометрический смысл. Правила вычисления дифференциала функции. 19. Производная и дифференциал высших порядков. 20. Теоремы Ферма, Ролля, Лагранжа, Коши. 21. Правило Лопиталя. 22. Формулы Тейлора и Маклорена. 23. Исследование поведения функций с помощью производной. Возрастающие и убывающие функции, признак монотонности. 24. Точки локального экстремума функции. Необходимые и достаточные условия существования экстремума функции. 25. Понятие выпуклой функции. Точки перегиба функции. 26. Асимптоты графика функции. Общая схема исследования функций с помощью производной. 27. Первообразная функции. Определение неопределенного интеграла. Основные свойства неопределенного интеграла. 28. Методы интегрирования. Метод замены переменной интегрирования. Интегрирование по частям. 29. Определение определенного интеграла, основные свойства. 30. Интеграл с переменным верхним пределом. 31. Формула Ньютона-Лейбница. 32. Замена переменной интегрирования в определенном интеграле. 33. Формула интегрирования по частям в определенном интеграле. 34. Понятие несобственных интегралов. 35. Основные понятия и определения функций многих переменных. 36. Понятие предела и непрерывности функций многих переменных. 37. Частные производные 1-го и 2-го порядков функций многих переменных. Понятие полного дифференциала функции многих переменных. 38. Экстремум функций многих переменных на примере функций двух переменных. 39. Необходимые и достаточные условия существования локального экстремума функции двух переменных 40. Определение параметров эмпирических зависимостей методом наименьших квадратов.
II. Линейная алгебра.
41. Понятие матрицы. Основные определения. 42. Действия над матрицами. Определение равенства матриц. Линейные операции над матрицами (сложение и вычитание матриц, умножение матрицы на действительное число). 43. Умножение матриц. Свойства произведения матриц. 44. Определение операции транспонирования матриц. Свойства операции транспонирования матриц. 45. Понятие определителя матрицы. Определители 1-го, 2-го и 3-го порядков. Определители n -го порядка. 46. Определение минора и алгебраического дополнения элемента матрицы. 47. Свойства определителей. 48. Понятие обратной матрицы. Определение невырожденной матрицы. Правило вычисления обратной матрицы. 49. Общие свойства обратной матрицы. 50. Решение систем линейных уравнений. Основные понятия, терминология и определения. 51. Решение систем n линейных уравнений с n неизвестными матричным способом.
52. Метод Крамера для решения систем n линейных уравнений с n неизвестными. 53. Метод Гаусса для решения систем n линейных уравнений с n неизвестными. 54. Теорема Кронекера – Капелли (без доказательства). 55. Примеры экономических приложений методов линейной алгебры. Модель Леонтьева многоотраслевой экономики. 56. Прямоугольная и полярная системы координат. Понятие уравнения линии. 57. Простейшие задачи аналитической геометрии. Расстояние между двумя точками. Деление отрезка в данном отношении. Площадь треугольника. 58. Линии первого порядка. Общее уравнение линии первого порядка в прямоугольной системе координат. 59. Уравнение прямой линии с угловым коэффициентом. Уравнение прямой, проходящей через заданную точку в данном направлении. Уравнение прямой, проходящей через две точки. Уравнение прямой линии в отрезках. 60. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых линий. 61. Координаты точки пересечения двух прямых, заданных общими уравнениями. 62. Расстояние от заданной точки до прямой линии, заданной общим уравнением. 63. Линии второго порядка. Общее уравнение линий 2 – ого порядка в прямоугольной системе координат. 64. Определение окружности. Каноническое уравнение окружности в прямоугольной системе координат. 65. Определение эллипса. Каноническое уравнение эллипса в прямоугольной системе координат, смысл его параметров, понятия эксцентриситета и директрисы эллипса. Формулы для вычисления фокальных радиусов текущей точки эллипса. 66. Определение гиперболы. Каноническое уравнение гиперболы в прямоугольной системе координат, смысл её параметров, асимптоты гиперболы, понятия эксцентриситета и директрисы гиперболы. Формулы для вычисления фокальных радиусов текущей точки гиперболы. 67. Общее определение кривых второго порядка, основанное на использовании понятий эксцентриситет и директриса. 68. Каноническое уравнение параболы в прямоугольной системе координат, смысл её параметра. Уравнение директрисы параболы. 69. Анализ общего уравнения кривых второго порядка. Приведение его к канонической форме (теорема без доказательства). Примеры.
III. Теория вероятностей и математическая статистика
70. Вероятность как частота события. Классическая вероятностная модель. Аксиомы теории вероятностей 71. Сумма событий. Совместные и несовместные события. Теорема сложения для классической модели. Следствия теоремы сложения. 72. Произведение событий. Зависимые и независимые события. Понятие условной вероятности. Теорема умножения для классической модели. Следствия теоремы умножения. 73. Формула полной вероятности. 74. Теорема Байеса. 75. Повторение испытаний. Формула Бернулли. 76. Случайные величины, их виды и примеры. 77. Функция распределения как универсальная характеристика случайных величин и ее свойства. 78. Плотность распределения непрерывной случайной величины и ее свойства. 79. Математическое ожидание случайной величины, мода, медиана. 80. Свойства математического ожидания. 81. Дисперсия случайной величины, среднее квадратическое отклонение. 82. Свойства дисперсии. 83. Равномерное распределение случайной величины и его параметры. 84. Биномиальное распределение случайной величины и его параметры. 85. Распределение Пуассона и его параметры. 86. Нормальное распределение случайной величины и его параметры. 87. Закон распределения системы двух случайных величин. 88. Функция распределения системы двух случайных величин. 89. Условные законы распределения системы двух случайных величин. 90. Числовые характеристики системы двух случайных величин. 91. Регрессия и корреляция. Коэффициент корреляции и его свойства. 92. Линейная регрессия. 93. Неравенство Чебышева. 94. Основные предельные теоремы. Центральная предельная теорема. 95. Генеральная совокупность и выборка (основные понятия). Способы организации выборок. Вариационный ряд. 96. Эмпирическая функция распределения и ее свойства. Гистограмма. Полигон частот. 97. Состоятельные и несмещенные оценки для математического ожидания и дисперсии. 98. Состоятельная и несмещенная оценка для вероятности. 99. Доверительный интервал. Доверительная вероятность. 100. Доверительный интервал для математического ожидания при известном σ. 101. Распределение Стьюдента. Доверительный интервал для математического ожидания при неизвестном σ. 102. Распределение 103. Доверительный интервал для вероятности. 104. Общая задача проверки гипотез. Критическая область и область принятия решений. 105. Проверка гипотез о законе распределения (критерий Пирсона). Список рекомендуемой литературы
1. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 1: Учеб. пособие для вузов / П.Е.Данко, А.Г.Попова, Т.Я.Кожевникова. – 6-е изд. – М.: ООО «Издательство Оникс»: ООО Издательство «Мир и Оразование», 2006 2. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 2: Учеб. пособие для вузов / П.Е.Данко, А.Г.Попова, Т.Я.Кожевникова. – 6-е изд. – М.: ООО «Издательство Оникс»: ООО Издательство «Мир и Оразование», 2006 3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие – 11-е изд., перераб. – М.: Высшее образование, 2006 4. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом приложении: Учебник. – 4-е изд., испр. – М.: Дело, 2003 5. Кремер Н.Ш. Высшая математика для экономических специальностей: учебник и практикум / Н.Ш.Кремер, Б.А.Путко, И.М.Тришин, М.Н.Фридман; под ред. Н.Ш. Кремера. – 3-е изд., перераб. и доп. – М.: Издательство Юрайт; Высшее образование, 2010 6. Кремер Н.Ш., Путко Б.А., Тришин И.М. Математика для экономистов: от Арифметики до Эконометрики: учеб.-справоч. пособие / под ред. проф. Н.Ш. Кремера. – М.: Высшее образование, 2009 7. Математика для экономистов. Задачник: учебно-методическое пособие / кол. авторов; под ред. С.И.Макарова, М.В.Мищенко. – М.: КРОКУС, 2008. – 360 с. 8. Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями: Учебное пособие. – Москва: ИКЦ «МарТ»; Ростов-н/Д: Издательский центр «МарТ», 2005 9. Практикум по высшей математике для экономистов: Учеб. пособие для вузов / Кремер Н.Ш., Тришин И.М., Путко Б.А. и др.; Под ред. проф. Н.Ш.Кремера. – М.:ЮНИТИ-ДАНА, 2005 10. Трофимов В.В., Данко С.П., Колесник В.А. Математика. Учебное пособие для студентов специальностей гуманитарных направлений – М.: ИКЦ «МарТ»; Ростов-н/Д: Издательский центр «МарТ», 2007 11. Шипачев В.С. Высшая математика: Учеб для вузов / В.С.Шипачев. – 6-е изд., стер. – М.: Высш. шк., 2003 1.7. Примерные задания контрольных работ для студентов Заочной формы обучения
1. Найти предел функции. а)
б)
2. Найти производную функции. а) б)
3. Найти вторую производную функции. а) б)
4. Записать дифференциал второго порядка функции
5. Вычислить интегралы. а) в)
6. Найти матрицу С = А ´–3 В, где А =
7. Решить систему линейных уравнений:
а) по формулам Крамера; б) методом Гаусса.
8. Решить матричное уравнение:
9. Даны три вектора:
10. Составить уравнение плоскости, проходящей через точку
11. Решить задачу об использовании ресурсов: а) геометрическим методом: б) симплексным методом. Для изготовления двух видов продукции Р 1 и Р 2 используют четыре вида ресурсов S 1, S 2, S 3 и S 4. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице.
Прибыль, получаемая от реализации единицы продукции Р 1 и Р 2, составляет m и n рублей соответственно. Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.
12. Группа состоит из т студентов факультета УЭФ, п студентов факультета АПК и (т + п) студентов факультета ПЭФ. Какова вероятность того, что 3 первых студента, явившихся на экзамен, окажутся: а) с факультета ПЭФ; б) двое с факультета АПК и один с факультета УЭФ?
13. Экзаменационный билет содержит 3 вопроса. Вероятность того, что студент ответит на первый, второй вопросы, равна по
14. Деталь, необходимая для сборки прибора, поступает с двух автоматов, производительность которых одинакова. Вычислить вероятность поступления на сборку стандартной детали, если первый из автоматов дает в среднем
15. Заданы математическое ожидание М и среднее квадратическое отклонение
16. Самостоятельно собрать данные о длине слов в книгах какого-либо писателя (объем выборки должен быть п ≥ 50). (В решении обязательно следует указать писателя и те его произведения, из которых делалась выборка). Необходимо: 1) Провести первичную обработку выборки: построить вариационный ряд, определить размах выборки, построить статистический ряд, записать эмпирический закон распределения. 2) Провести частотную табуляцию выборки, построить гистограмму и полигон частот выборки. 3) Построить выборочную функцию распределения. 4) Вычислить выборочные характеристики: среднее выборочное, выборочную дисперсию, несмещенную оценку дисперсии. 5) При уровне значимости α = 0,05 проверить гипотезу о том, что длина слов распределена по нормальному закону. Параметры распределения оцениваются по выборке: математическое ожидание – по среднему выборочному, среднее квадратическое отклонение – по квадратному корню из несмещенной оценки дисперсии.
1.8. Методические указания для студентов Методические указания для студентов Очной формы обучения
Успешное освоение курса предполагает активное и творческое участие студента на всех этапах обучения путем планомерной повседневной работы на лекциях, практических занятиях и при самостоятельной подготовке. При подготовке к практическим занятиям студентам следует внимательно поработать с текстом лекции, учебным материалом рекомендуемого учебника, разобрать решение ключевых задач, выписать необходимые формулы, выполнить задания для самостоятельного решения, подготовить теоретический материал, предложенный для самостоятельного изучения, подготовить вопросы, которые вызвали затруднения. Студенту рекомендуется вовремя выполнять расчетно-графические задания (РГЗ), готовиться к контрольным работам, текущему, рубежному контролю. При подготовке к защите РГЗ, зачету или экзамену следует изучить конспект лекций и просмотреть литературу, рекомендуемую преподавателем.
Методические указания для студентов Заочной формы обучения
В соответствии с учебным планом студенты заочной формы обучения изучают дисциплину «Математика» на 1 и 2 курсах (или только на 1 курсе – при сокращенных сроках обучения). Содержание учебного материала определяют требования пГОС ВПО по специальности 080504 – Государственное и муниципальное управление. Рабочим учебным планом для заочной формы обучения в каждом семестре предусмотрено выполнение письменной контрольной работы. Цель выполнения контрольных работ состоит в закреплении и проверке знаний, полученных студентами в процессе самостоятельного изучения учебного материала. Прежде чем приступить к выполнению работы, студент должен проработать рекомендуемую литературу. Задания в контрольной работе охватывают основные темы курса. Контрольную работу необходимо выполнить самостоятельно и представить точно в установленные графиком сроки. Номер индивидуального варианта задач контрольных работ выбирается по двум последним цифрам зачетной книжки студента: т и п. Контрольная работа составлена в десяти вариантах. В приведенной ниже таблице устанавливается соответствие варианта и значение чисел т и п.
Контрольная работа, выполненная не по своему варианту, не зачитывается.
Контрольная работа выполняется и оформляется при соблюдении правил: 1. Контрольная работа выполняется от руки (или машинописным способом) в отдельной ученической тетради (или на белых листах формата А4) предпочтительно пастой (чернилами) синего цвета. 2. На обложке записывается
3. Номер варианта выбирается по двум последним цифрам зачетной книжки студента. 4. Задачи располагаются в порядке, указанном в задании на контрольную работу под своими номерами. 5. Условие задачи полностью, без сокращений переписывается из задания на контрольную работу. После условия задачи отдельной строкой записывается слово «Решение», а далее последовательно по пунктам с подробным объяснением, без сокращений слов, аккуратно и четко, со ссылками на необходимые теоремы, утверждения, определения понятий и формулы излагается ход решения. 6. Оставляются поля для замечаний преподавателя. Выполненную контрольную работу необходимо предъявить в учебное отделение, сотрудники которого передадут работу преподавателю для проверки. Преподаватель делает замечания к решениям задач, указывает на недостатки оформления и выносит заключение о допуске работы к зачету или возвращает ее студенту на доработку. Студент учитывает и устраняет замечания в той же тетради после заключения преподавателя, правильно и подробно излагая соответствующие преобразования и объяснения в разделе «Работа над ошибками». Зачет по контрольной работе студент получает лишь только после выполнения работы над замечаниями и собеседования с преподавателем. Студенты, не защитившие контрольную работу, к сдаче экзамена (зачета) по дисциплине «Математика» не допускаются.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 673; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.63.236 (0.174 с.) |
. Интегральная теорема Муавра–Лапласа. Функция Лапласа и ее свойства.
. Доверительный интервал для дисперсии.
в) 
г) 
в) 
г) 
.
; б) 
;
; г) 
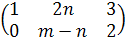, В = 
.
, 
, 
. Найти координаты вектора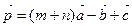 
и разложить его по векторам 
и 
.
и 
.
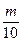, на третий – 
. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить: а) на все вопросы; б) по крайней мере на два вопроса.
% нарушений, второй – 
нормально распределенной случайной величины х. Найти: 1) вероятность того, что х примет значение, принадлежащее интервалу 
; 2) вероятность того, что абсолютная величина отклонения 
окажется меньше 
, если М = 12, 
, 
, 
, 
.
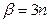