
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выборочная функция распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для эмпирической случайной величины, заданной эмпирическим законом распределения, можно записать и построить выборочную функцию распределения. Функция распределения случайной величины задана на всей числовой оси и определяется равенством: F (x) = P (ξ < x), т.е. функция распределения равна вероятности того, что случайная величина примет значение меньше х. При x ≤ 1 событие ξ 20< 1 невозможно, т.к. нет значений ξ20 меньше 1, а вероятность невозможного события равна нулю, следовательно, F (x) = P (ξ 20< 1) = 0. На промежутке 1 < x ≤ 2 событие ξ 20< 2 состоит в том, что ξ 20 принимает значение 1, соответственно вероятность такого события равна 0,1, т.е. F (x) = P (ξ 20< 2) = 0,1. На промежутке 2 < x ≤ 4 событие ξ 20< 4 состоит в том, что ξ 20 принимает значение 1 или 2, соответственно вероятность такого события равна F (x) = P (ξ 20< 4) = 0,3. На промежутке 4 < x ≤ 5 событие ξ 20< 5 состоит в том, что ξ 20 принимает значение или 1, или 2, или 4. Соответственно вероятность такого события равна F (x) = P (ξ 20< 5) = 0,65. На промежутке 5 < x ≤ 6 событие ξ 20< 6 состоит в том, что ξ 20 принимает значение или 1, или 2, или 4, или 5. Соответственно вероятность такого события равна F (x) = P (ξ 20< 6) = 0,75. И.т.д. Таким образом, выборочная функция распределения имеет вид:
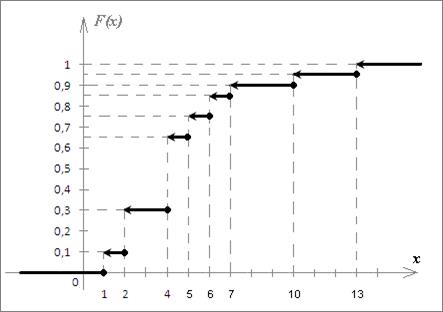
Определив значения функции распределения на всей числовой оси, можно построить ее график (Рис.1).
Рис.1.
График выборочной функции распределения имеет ступенчатый вид и строится в виде отрезков: левее наименьшего значения (х = 1) значение функции равно 0 (т.е. график совпадает с горизонтальной осью); в каждой следующей точке xi происходит скачек на величину вероятности νi.. Например, в точке х 1 = 1 скачек равен ν 1 = . 0,1(см. эмпирический закон распределения); в точке х 2 = 2 скачек равен ν 2 = 0,2; в точке х 3 = 4 скачек равен ν 3 = 0,2; и т.д. Правее наибольшего значения (х 8 = 13) функция равна единице. Стрелки и точки на концах отрезков показывают, что функция определена на полуинтервалах. Частотная табуляция При большом объеме выборки ее элементы группируют. Для этого интервал, содержащий все значения выборки (от x min до x max), разбивают на т непересекающихся интервалов. При этом считается, что правая граница интервала принадлежит следующему интервалу (последний интервал содержит обе свои границы). Число интервалов т можно выбрать произвольно или найти по формуле Стерджесса:
где п – объем выборки. Тогда длина каждого интервала равна После этого подсчитывают частоты nj – количество элементов выборки, попавших в j -й интервал, и накопленные частоты. Результаты сводят в таблицу частот группированной выборки. Процесс формирования такой таблицы называется частотной табуляцией. Проведем частотную табуляцию выборки из нашего примера. Определим число интервалов по формуле Стерджесса:
Число т должно быть целым, т.е. либо 5, либо 6. Т.к. размах выборки равен Таким образом, разбиваем интервал значений выборки (от 1 до 13) на В первом столбце таблицы записываем номер интервала от 1 до 6. Затем, используя статистический ряд выборки, определяем границы интервалов и записываем их во втором столбце: 1) наименьшее значение выборки равно 1, значит, начинаем построение с 1: от 1 → 1 + 2 = 3 → до 3; 2) от 3 → 3 + 2 = 5 → до 5; 3) от 5 → 5 + 2 = 7 → до 7; 4) от 7 → 7 + 2 = 9 → до 9; 5) от 9 → 9 + 2 = 11 → до 11; 6) от 11 → 11 + 2 = 13 → до 13. Наибольшее значение выборки равно 13, значит, интервалы определены верно. В третьем столбце запишем середины полученных интервалов. Середину интервала (а; b) можно найти по формуле:
Таблица 1
В четвертом столбце записываем интервальные частоты, т.е. частоты попадания элементов выборки в данный интервал, например: в 1-й интервал попадают значения 1 и 2, при этом значение 1 встречается 2 раза (п 1 = 2)[15], значение 2 встречается 4 раза (п 2 = 4), поэтому первая интервальная частота равна во 2-й интервал попадают значения 3 и 4, при этом значение 3 вообще не встречается в выборке, значение 4 встречается 7 раз (п 3 = 7), поэтому вторая интервальная частота равна в 3-й интервал попадают значения 5 и 6, при этом значение 5 встречается 2 раза (п 4 = 2), значение 6 встречается также 2 раза (п 4 = 2), поэтому третья интервальная частота равна В пятом столбце Таблицы 1 записываем накопленные частоты по принципу: j -я частотанакопл. =. (j – 1)-я частотанакопл+ j -я частотаинт. Например: 1-я накопленная частота равна 6, т.к. предыдущая накопленная частота равна 0 (ее нет), а 1-я интервальная частота равна 6 (см. 4-й столбец): 0 + 6 = 6; 2-я накопленная частота равна 13, т.к. предыдущая (1-я) накопленная частота равна 6, а 2-я интервальная частота равна 7 (см. 4-й столбец): 6 + 7 = 13; 3-я накопленная частота равна 17, т.к. предыдущая (2-я) накопленная частота равна 13, а 3-я интервальная частота равна 4 (см. 4-й столбец): 13 + 4 = =17 и т.д. На этом частотная табуляция выборки заканчивается.
Вариационный ряд можно представить и графически, построив полигон и гистограмму частот выборки. Графическое изображение выборки позволяет визуально оценить плотность вероятности распределения генеральной совокупности. Для построения полигона и гистограммы выборки в рассмотренном примере воспользуемся данными данным Таблицы 1. На координатной плоскости по горизонтальной оси откладываем значения выборки (xi), по вертикальной оси – частоты (ni) (Рис.2). Единичные отрезки по осям могут быть различны (их размер выбирают, руководствуясь принципом наглядности).
Рис. 2 Гистограмма. На отрезках, равных интервалам Таблицы 1 (2-й столбец), строятся прямоугольники, высота которых равна соответствующим интервальным частотам (4-й столбец Таблицы 1). Полученный набор прямоугольников называется гистограммой выборки. Полигон. Соединим отрезками середины верхних сторон прямоугольников гистограммы. Полученная ломаная линия называется полигоном выборки (на Рис.2 она обозначена красным цветом).
Проверка гипотезы о законе распределения
Рассмотрим процесс проверки гипотезы о законе распределения на примере из предыдущего раздела. Пример. Книгу «Винни-Пух и все-все-все» открывали на случайной странице, где выбирали случайное слово. При этом фиксировали длину этого слова. В результате 20 опытов получена следующая выборка: 4, 1, 4, 5, 1, 13, 4, 10, 2, 4, 7, 2, 2, 4, 6, 4, 5, 6, 2, 4. Требуется: 1) Вычислить выборочные характеристики: среднее выборочное, выборочную дисперсию, несмещенную оценку дисперсии. 2) При уровне значимости α = 0,05 проверить гипотезу о том, что длина слов распределена по нормальному закону. Параметры распределения оцениваются по выборке: математическое ожидание – по среднему выборочному, среднее квадратическое отклонение – по квадратному корню из несмещенной оценки дисперсии.
Выборочные характеристики Выборочное среднее может быть найдено по формуле
где k – число различных элементов выборки, п – объем выборки. Выборочная дисперсия:
Несмещенная оценка дисперсии:
Обычно процесс вычисления выборочных характеристик оформляют в виде таблицы (Таблица 2). В нашем примере k = 8, п = 20, значения xi и ni приведены в статистическом ряде выборки. Заполнение расчетной таблицы начинаем с заполнения столбцов xi и ni, записывая в них данные статистического ряда. Затем вычисляем произведения xi · ni и результаты заносим в третий столбец. В последней строке суммируем данные, получили 90. Теперь вычисляем среднее выборочное, поделив получившуюся сумму на объем выборки, т.е. на 20.
Теперь, вычислив среднее выборочное, заполняем четвертый столбец, записывая в него соответствующие разности
Таблица 2
В пятом столбце записываем квадраты значений предыдущего столбца, например:
Далее умножаем полученные значения пятого столбца на соответствующие частоты (из второго столбца) и результат записываем в последнем столбце, например:
В последней строке суммируем данные последнего столбца, получили 165,00. Теперь вычислим выборочную дисперсию:
Несмещенную оценку дисперсии найдем, зная выборочную дисперсию:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 4576; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.116 (0.011 с.) |

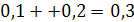 , т.е.
, т.е.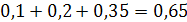 , т.е.
, т.е. , т.е.
, т.е.
 ,
,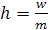 , где w – размах выборки.
, где w – размах выборки.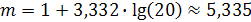 .
.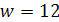 , то удобнее взять т = 6, т.к. в этом случае длина одного интервала
, то удобнее взять т = 6, т.к. в этом случае длина одного интервала  . Если мы возьмем т = 5, то
. Если мы возьмем т = 5, то  , что не очень удобно, т.к. значения выборки целые.
, что не очень удобно, т.к. значения выборки целые.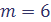 интервалов с шагом
интервалов с шагом 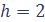 . Результаты заносим в таблицу (Таблица 1).
. Результаты заносим в таблицу (Таблица 1). , например: для 1-го интервала
, например: для 1-го интервала  ; для 2-го интервала
; для 2-го интервала 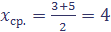 и т.д.
и т.д.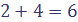 ; в первой строке записываем 6;
; в первой строке записываем 6;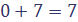 ; во второй строке записываем 7;
; во второй строке записываем 7; ; в третьей строке записываем 4 и т.д.
; в третьей строке записываем 4 и т.д.
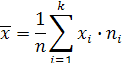
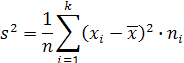
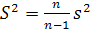 .
.
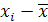 , например:
, например: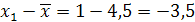 Записываем в первой строке -3,5;
Записываем в первой строке -3,5; Записываем во второй строке -2,5 и т.д.
Записываем во второй строке -2,5 и т.д.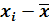

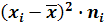
 Записываем в первой строке 12,25;
Записываем в первой строке 12,25; Записываем во второй строке 6,25 и т.д.
Записываем во второй строке 6,25 и т.д.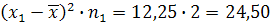 Записываем в первой строке 24,50;
Записываем в первой строке 24,50;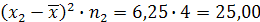 Записываем во второй строке 25,00 и т.д.
Записываем во второй строке 25,00 и т.д.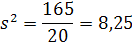
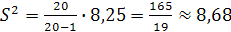 .
.


