
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ЛОДУ второго порядка с постоянными коэффициентамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим процесс нахождения общего решения ЛОДУ второго порядка с постоянными коэффициентами на примерах.
Пример 1. Решить уравнение Решение. Составим характеристическое уравнение:
Решаем его:
Записываем общее решение данного уравнения:
где С 1 и С 2 – произвольные независимые постоянные.
Пример 2. Решить уравнение Решение. Составим характеристическое уравнение:
Решаем его:
Записываем общее решение данного уравнения:
где С 1 и С 2 – произвольные независимые постоянные. Пример 3. Решить уравнение Решение. Составим характеристическое уравнение:
Дискриминант равен: Найдем a и b:
Тогда общее решение записывается в виде:
где С 1 и С 2 – произвольные независимые постоянные.
§ 10. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Дифференциальное уравнение второго порядка называются линейным неоднородным дифференциальным уравнением (ЛНДУ) с постоянными коэффициентами, если оно имеет вид:
где p и q – некоторые действительные числа, r (x) – некоторая функция. Для каждого ЛНДУ вида Это имеет существенное значение, т.к. общее решение ЛНДУ напрямую связано с общим решением соответствующего ЛОДУ. Универсальным методом для нахождения общего решения ЛНДУ является метод вариации постоянных, который заключается в следующем. Пусть мы нашли общее решение соответствующего ЛОДУ:
Тогда общее решение ЛНДУ находят в виде:
предполагая, что постоянные С 1 и С 2 зависят от переменной х, т.е. являются функциями. При этом функции С 1(х) и С 2(х) могут быть найдены поэтапно. Сначала находят их первые производные из системы уравнений:
где r (x) – функция, стоящая в правой части исходного ЛНДУ. Затем, решая дифференциальные уравнения первого порядка, находят сами функции.
В заключении найденные функции С 1(х) и С 2(х) подставляют в общее решение ЛОДУ. Рассмотрим применение метода вариации постоянных на примере.
Пример. Решить уравнение Решение. 1. Решим соответствующее ЛОДУ:
2. Выпишем отдельно функции у 1 и у 2, найдем их производные:
3. Составим систему уравнений и решим ее:
Получили, что С 1' = –1, С 2' = 1/ е х = е –х.
4. Решим дифференциальные уравнения:
5. Найденные С 1 и С 2 подставим в общее решение ЛОДУ, получим искомое общее решение ЛНДУ:
Следует отметить, что метод вариации постоянных позволяет решить любое ЛНДУ вне зависимости от r (x) – функции, стоящей в правой части исходного ЛНДУ. Однако этот метод достаточно сложен, поэтому в ряде случаев для отыскания общего решения ЛНДУ применяют второй метод – метод решения ЛНДУ со специальной правой частью. Этот метод основан на теореме, которая определяет структуру общего решения ЛНДУ. Теорема (Структура общего решения ЛНДУ). Общее решение ЛНДУ есть сумма общего решения соответствующего ЛОДУ и какого-либо частного решения исходного ЛНДУ:
Таким образом, нам надо найти общее решение ЛОДУ, что сделать не трудно, и отыскать какое-нибудь частное решение исходного ЛНДУ. Вид этого частного решения устанавливается по виду правой части исходного ЛНДУ, т.е. по виду функции r (x). Рассмотрим некоторые возможные случаи. 1. Функция r (x) – многочлен степени т:
Тогда частное решение следует искать в виде
где k – число корней характеристического уравнения, равных нулю, т.е. k = 0, если q ¹ 0 k = 1, если q = 0, p ¹ 0 k = 2, если q = 0, p = 0. Пример. Найти частное решение уравнения Решение. Правая часть уравнения – многочлен первой степенны, следовательно, частное решение надо искать в виде
Определим значение параметра k: т.к. в левой части дифференциального уравнения q = 0, p = –3 ¹ 0, то k = 1, тогда частное решение имеет вид
Чтобы найти числа С 0 и С 1, найдем производные от нашего у ч.н. и подставим их в исходное уравнение:
Соответствующие коэффициенты в правой и левой частях равенства должны быть равны, следовательно, можно записать систему уравнений:
Решая эту систему, получим С 1 = – 1, С 0 = – 1. Теперь, зная значения коэффициентов С 0 и С 1, подставим их в уравнение
2. Функция r(x) – произведение числа на показательную функцию:
В этом случае частное решение следует искать в виде
где n – число корней характеристического уравнения, равных а, т.е. п = 0, если k 1 ¹ а, k 2 ¹ а, п = 1, если k 1 = а, k 2 ¹ а или k 1 ¹ а, k 2 = а п = 2, если k 1 = k 2 = а
Пример. Найти частное решение уравнения Решение. Правая часть уравнения – это произведение числа на показательную функцию, следовательно, частное решение надо искать в виде
Число а = 3 по условию. Чтобы определить значение параметра п, надо найти корни характеристического уравнения:
Т.к. оба корня характеристического уравнения неравны числу а, то п = 0, тогда частное решение имеет вид:
Чтобы найти число С 0, найдем производные от нашего у ч.н. и подставим их в исходное уравнение:
Подставим С 0 = 1 в уравнение
3. Функция r (x) – сумма тригонометрических функций вида:
где А, В, b – некоторые действительные числа, причем b ¹ 0. Тогда частное решение следует искать в виде
где s = 1, если p = 0, q > 0, s = 0, во всех других случаях.
Пример. Найти частное решение уравнения Решение. Правая часть уравнения – это тригонометрическая функций вида:
частное решение следует искать в виде
Параметр s = 0, т.к. не выполняется условие p = 0, q > 0, следовательно,
Чтобы найти числа С 0 и С 1, найдем производные от нашего у ч.н. и подставим их в исходное уравнение:
Коэффициенты при соответствующих тригонометрических функциях в правой и левой частях равенства должны быть равны, следовательно, можно записать систему уравнений:
Решая эту систему, получим С 1 = 0,1 и С 0 = 0,3. Теперь, зная значения коэффициентов С 0 и С 1, подставим их в уравнение
Подводя итог, составим алгоритм нахождения общего решения ЛНДУ второго порядка с постоянными коэффициентами со специальной правой частью: 1. Привести уравнение к виду 2. Составить соответствующее однородное уравнение: 3. Найти 4. Используя Таблицу 2, определить общий вид частного решения ЛНДУ. 5. Найти числа Сi и записать 6. Записать искомое общее решение ЛНДУ по формуле:
Таблица 2 Таблица частных решений
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1941; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.134.162 (0.011 с.) |





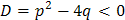
 ,
, 

 .
.

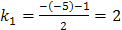 ,
,  .
. ,
, .
.

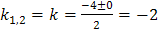 .
. ,
, .
. .
. .
. .
. ,
, ,
, , для которого легко можно найти общее решение (см.алгоритм).
, для которого легко можно найти общее решение (см.алгоритм).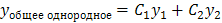 .
. ,
, С 1' · y 1
С 1' · y 1
 .
.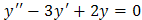


 ,
, 
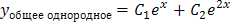
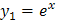 ,
, 
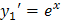 ,
, 



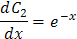



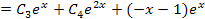 .
.

 ,
,
 .
.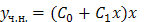 .
. ,
, .
.


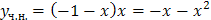 .
.
 ,
,
 .
.


 .
. ,
,

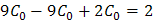
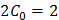

 .
.
 ,
,
 , где b = 1.
, где b = 1. .
. .
. ,
, .
.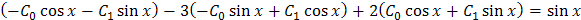


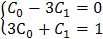
 .
.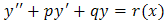 , где p и q – некоторые действительные числа, r (x) – некоторая функция.
, где p и q – некоторые действительные числа, r (x) – некоторая функция. .
. – общее решение этого однородного уравнения, используя Таблицу 1.
– общее решение этого однородного уравнения, используя Таблицу 1.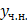 – частное решение исходного неоднородного уравнения.
– частное решение исходного неоднородного уравнения.



