
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ЛНДУ второго порядка с постоянными коэффициентамиСодержание книги
Поиск на нашем сайте
Со специальной правой частью
Пример. Найти общее решение уравнения Решение. 1. Уравнение уже приведено к нужному виду. 2. Соответствующее ЛОДУ имеет вид: Его характеристическое уравнение:
3. По таблице 1 находим вид общего решения ЛОДУ:
где С 1 и С 2 – произвольные независимые постоянные. 4. Правая часть исходного уравнения
Параметр k = 0, т.к. q = 3 ¹ 0, следовательно,
5. Чтобы найти числа С 0, С 1 и С 2, найдем производные от нашего у ч.н. и подставим их в исходное уравнение:
Соответствующие коэффициенты в правой и левой частях равенства должны быть равны, следовательно, можно записать систему уравнений:
Решая эту систему, получим С 2 = 0,5; С 1 = – 1,5; С 0 = 1,75. Теперь, зная значения коэффициентов С 0, С 1 и С 2, подставим их в уравнение
6. Искомое общее решение ЛНДУ имеет вид:
В заключение приведем одно замечание, которое часто применяется при решении дифференциальных уравнений: Если правая часть уравнения
т.е.
Приложение 1 Вывод формул общего решения ЛОДУ второго порядка с постоянными коэффициентами
Случай 1. Дискриминант больше нуля, следовательно, корни k 1 и k 2 действительные и различные:
В этом случае частными решениями ЛОДУ являются функции
где С 1 и С 2 – произвольные независимые постоянные.
Случай 2. Дискриминант равен нулю, следовательно, корни k 1 и k 2 действительные и равные:
В этом случае имеем лишь одно частное решение Покажем, что наряду с Действительно, подставим функцию
ß
Но k – это корень характеристического уравнения, следовательно,
Это значит, что функция Таким образом, у нас есть два различных частных решения ЛОДУ:
где С 1 и С 2 – произвольные независимые постоянные.
Случай 3. Дискриминант меньше нуля. В этом случае уравнение не имеет действительных корней, корни квадратного уравнения в этом случае – комплексные числа. Комплексные числа – особое числовое множество, в котором можно извлекать квадратный корень из отрицательных чисел. В этом множестве есть элемент i, который называется мнимая единица и обладает свойством: При таких условиях можно извлекать корень из любого отрицательного числа: Любое комплексное число можно представить в виде
где a и b – действительные числа. При этом a называется действительной частью комплексного числа, bi называется мнимой частью комплексного числа. Нетрудно доказать, что привычное нам множество действительных чисел R является подмножеством множества комплексных чисел С: R Ì С. Но вернемся к нашему ЛОДУ, для которого характеристическое уравнение имеет отрицательный дискриминант: Найдем корни характеристического уравнения
Таким образом, характеристическое уравнение имеет два различных комплексных корня где Следовательно, частными решениями исходного ЛОДУ будут функции К сожалению, эти частные решения содержат мнимую единицу, что не очень хорошо, т.к. мы должны найти решение ЛОДУ на множестве действительных чисел. Попробуем преобразовать наши частные решения так, чтобы они не содержали мнимую единицу. Воспользуемся формулами Эйлера:
Тогда
Теперь мы можем найти два действительных частных решения:
В итоге общее решение ЛОДУ имеет вид
где С 1 и С 2 – произвольные независимые постоянные,
Приложение 2 Раздаточный материал
ЛОДУ:
Характеристическое уравнение:
Таблица возможных общих решений
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1090; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |



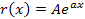
 ,
,
 где А, В, b – числа, b ¹ 0
где А, В, b – числа, b ¹ 0


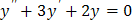


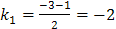 ,
,  .
.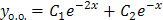 ,
, – многочлен второй степени, тогда согласно Таблице 2, частное решение ЛНДУ ищем в виде:
– многочлен второй степени, тогда согласно Таблице 2, частное решение ЛНДУ ищем в виде: .
. .
. ,
, .
.



 .
. .
. является суммой некоторых функций:
является суммой некоторых функций:  , то частное решение этого уравнения есть сумма частных решений уравнений
, то частное решение этого уравнения есть сумма частных решений уравнений , где i =1, 2, … п,
, где i =1, 2, … п, .
. k 1 ¹ k 2
k 1 ¹ k 2 и
и  . Следовательно, общее решение ЛОДУ имеет вид:
. Следовательно, общее решение ЛОДУ имеет вид: ,
, k 1 = k 2 = k
k 1 = k 2 = k , а для нахождения общего решения ЛОДУ нам необходимо два различных частных решения. Как найти второе?
, а для нахождения общего решения ЛОДУ нам необходимо два различных частных решения. Как найти второе? .
. , найдя предварительно ее производные. Имеем:
, найдя предварительно ее производные. Имеем:


 .
. ; кроме того, по теореме Виета
; кроме того, по теореме Виета  или
или  , т.е.
, т.е.  . Тогда
. Тогда .
. является решением ЛОДУ.
является решением ЛОДУ. ,
, , откуда
, откуда  .
. .
. ,
,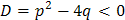 .
. :
:
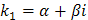 и
и  ,
, ,
, 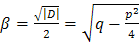 .
. и
и  .
. ,
,  .
. ,
,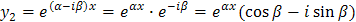 .
. и
и  .
. ,
,


