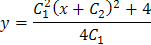Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 3. Дифференциальные уравнения второго порядка. Решение ду, допускающих понижение порядкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оглавление
§ 7. Дифференциальные уравнения второго порядка Дифференциальное уравнение второго порядка Теорема о существовании и единственности решения дифференциального уравнения второго порядка Задача Коши Общее решение дифференциального уравнения второго порядка Частное решение дифференциального уравнения второго порядка Пример § 8. Дифференциальные уравнения второго порядка, допускающие понижение порядка 1. Уравнение 2. Уравнение 3. Уравнение § 7. Дифференциальные уравнения второго порядка
Дифференциальное уравнение второго порядка связывает независимую переменную, искомую функцию и ее первую и вторую производные. В частных случаях в уравнении могут отсутствовать x, Дифференциальное уравнение второго порядка в общем случае имеет вид:
или, если это возможно, в виде, разрешенном относительно второй производной:
Как и в случае уравнения первого порядка, для такого уравнения справедлива теорема. Теорема о существовании и единственности решения ДУ второго порядка. Пусть в уравнении
Задача нахождение решения уравнения Общим решением дифференциального уравнения второго порядка называется функция 3) она является решением этого дифференциального уравнения при любых конкретных значениях постоянных С 1 и С 2; 4) каковы бы ни были начальные условия, существуют единственные значения постоянных С 1 = С10 и С 2 = С20 такие, что функция Значения постоянных С 10 и С 20 можно найти из системы уравнений
Частным решением дифференциального уравнения второго порядка называется всякое решение Рассмотрим на простейшем примере, какой вид имеет общее и частное решение дифференциального уравнения второго порядка. Пример. Найти решение уравнения Решение. Обозначим
Возвращаясь к исходной переменной, снова получим уравнение первого порядка:
Полученное общее решение зависит от двух произвольных постоянных С 1 и С 2. Для нахождения частного решения уравнения воспользуемся начальными условиями. В задаче дано, что у (1) = 2, подставляя это условие в общее решение С другой стороны, известно, что Из системы уравнений:
находим, что
В ходе решения данного примера мы свели решение дифференциального уравнения второго порядка к интегрированию уравнений первого порядка, что существенно упростило вычисления. Рассмотрим отдельно типы уравнений второго порядка, которые можно решать таким методом.
§ 8. Дифференциальные уравнения второго порядка, допускающие понижение порядка
Преобразование дифференциального уравнения второго порядка, в ходе которого с помощью замены переменной его сводят к уравнению первого порядка, называется понижением порядка. Простейшими уравнениями, допускающими понижение порядка, являются следующие: 1) 2) 3) Рассмотрим последовательно, как осуществляется понижение порядка и как интегрируется каждое из указанных уравнений.
1. Уравнение Принцип решения этого типа уравнений мы рассмотрели в примере. Введем новую функцию v (x), положив
Возвращаясь к замене, получим
или
Пример. Найти общее решение уравнения Решение. Пусть
Решая это уравнение первого порядка, получим:
Т.к.
2. Уравнение Это уравнение не содержит явно искомой функции у. Вводя, как и в предыдущем случае, новую функцию
Допустим, что найдено общее решение этого уравнения v = φ (x, C 1). Заменяя в этом решении функцию v на
Отсюда общее решение уравнения
Пример. Найти общее решение уравнения Решение. Пусть
Разделяя переменные и решая уравнение первого порядка, получим:
где Возвращаясь к первоначальной переменной
Таким образом, общее решение уравнения имеет вид:
Выделим из него частное решения, используя начальные условия. Во-первых, у (1) = 0, следовательно, Во-вторых, y ' (1) = 1, т.е. Решим систему уравнений:
Подставив найденные значения С 1 и С 2 в общее решение уравнения, получим искомое частное решение:
или
3. Уравнение Для понижения порядка уравнения введем новую функцию v (y), зависящую от у, полагая Продифференцируем это равенство по х, помня, что у является функцией от переменной х, т.е. v (y) – сложная функция:
Т.к. Подставляя выражения
Пусть функция
Интегрируя его, находим общий интеграл первоначального уравнения:
Пример. Найти общее решение уравнения Решение. Вводим новую неизвестную функцию v (y), полагая
Разделим переменные в получившемся уравнении:
Интегрируя, находим
Пусть
Выражая отсюда функцию v (y), получим
Произведем обратную замену
Разделяя переменные, получим:
Преобразовывая полученное выражение, выразим искомую функцию:
К дифференциальным уравнениям второго порядка сводится решение многих задач математики (например, задача о цепной линии), физики (некоторые задачи о движении тела, учитывающие сопротивление среды), экономической динамики и др.
Дифференциальные уравнения
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 7860; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.208.243 (0.008 с.) |



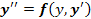
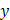 и
и  . Однако уравнение второго порядка обязательно должно содержать вторую производную
. Однако уравнение второго порядка обязательно должно содержать вторую производную  .
.
 .
. функция
функция  и ее частные производные по у и по
и ее частные производные по у и по  ) этой области, данное уравнение имеет единственное решение
) этой области, данное уравнение имеет единственное решение  , удовлетворяющее начальным условия: у (х 0) = у 0 и
, удовлетворяющее начальным условия: у (х 0) = у 0 и  .
. , которая зависит от двух произвольных постоянных С 1 и С 2 и удовлетворяет условиям:
, которая зависит от двух произвольных постоянных С 1 и С 2 и удовлетворяет условиям: является решением уравнения
является решением уравнения 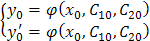 .
. уравнения
уравнения  при конкретных значениях постоянных С 1 = С10 и С 2 = С20.
при конкретных значениях постоянных С 1 = С10 и С 2 = С20. при условиях у (1) = 2,
при условиях у (1) = 2,  .
. , тогда
, тогда  , и уравнение примет вид
, и уравнение примет вид  или
или  . Решая это уравнение первого порядка, получим:
. Решая это уравнение первого порядка, получим:







 или
или  .
.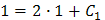 или
или  .
.
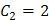 . Тогда искомое частное решение имеет вид:
. Тогда искомое частное решение имеет вид: .
. ;
; ;
; .
. .
.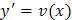 , тогда
, тогда 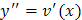 . Подставив полученные выражения в уравнение
. Подставив полученные выражения в уравнение 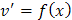 или
или 

 .
. или
или 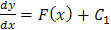


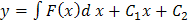 .
. .
. или
или  .
.
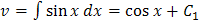 .
.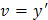 , то
, то 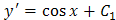 , тогда
, тогда
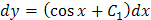
 .
. .
. и замечая, что
и замечая, что  .
. или
или 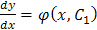 .
. .
.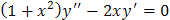 и выделить из него частное решение, удовлетворяющее начальным условиям у (1) = 0, y '(1) = 1.
и выделить из него частное решение, удовлетворяющее начальным условиям у (1) = 0, y '(1) = 1.




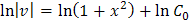
 ,
, .
. или
или  , откуда
, откуда
 .
. .
. или
или  .
. или
или  .
.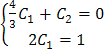 ↔
↔  ↔
↔ 

 .
. .
. .
. .
. , то
, то  .
. .
. является общим решением этого уравнения. Вспоминая, что
является общим решением этого уравнения. Вспоминая, что  ,получаем уравнение с разделяющимися переменными:
,получаем уравнение с разделяющимися переменными: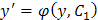 или
или  .
.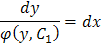
 .
.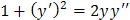 .
. .
.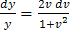 .
. ,
,
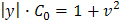
 .
. .
. .
. или
или  .
.

 .
.