
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение лнду второго порядка с постоянными коэффициентами и правой частью специального вида.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим ЛНДУ второго порядка с постоянными коэффициентами т.е. уравнение
Где p и g – некоторые числа согласно вышеприведенной теореме. Однако, для уравнений с постоянными коэффициентами существует более простой способ нахождения у*,если правая часть I. Cуть метода, называемого методом неопределенных коэффициентов, состоит в следующем: по виду правой части f(x) уравнения (24) записывают ожидаемую форму частного решения с неопределенными коэффициентами, затем подставляют его в уравнение (24) и из полученного тождества находят значение коэффициентов. Вариант 1. Правая часть имеет вид Уравнение (24) запишется в виде В этом случае частное решение y* ищется в виде
а) Пусть
После подстановки функции y* и ее производных в уравнение (25) и сокращения на Слева многочлен степени n с неопределенными коэффициентами, справа – многочлен степени n, но с известными коэффициентами. Приравнивая коэффициенты при одинаковых степенях, получим систему (n + 1) алгебраических уравнений для определения коэффициентов
б) Пусть
В левой части многочлен степени (n-1), а в правой многочлен степени n.Чтобы получить тождество многочленов в решении у* нужно иметь многочлен тоже степени (n-1), поэтому частное решение у* следует искать в виде
в) Пусть
Вариант 2. Правая часть уравнения (24) имеет вид
Можно показать, что в этом случае частное решение у* последнего уравнения следует искать в виде
r – число, равное кратности
Примечания: 1) При подстановке функции (28) в (27) приравнивают многочлены, стоящие перед одноименными тригонометрическими функциями в левой и правой частях уравнения. 2) Формула (28) сохраняется и в случаях, когда 3) Если правая часть уравнения (24) есть сумма вида I или II то для нахождения у* следует использовать теорему о наложении решений. Пример: Найдем общее решение
Поэтому частное решение данного уравнения имеет вид
4.Решение ЛНДУ n- го порядка Рассмотрим линейное неоднородное ДУ n-го
Теорема: Общее решение ЛНДУ n-го порядка равно сумме частного решения у* неоднородного уравнения и общего решения
Частное решение ЛНДУ n-го порядка может быть найдено, если известно общее решение Система уравнений для нахождения неизвестных
Однако, для ЛНДУ n – го порядка с постоянными коэффициентами, правая часть которого имеет специальный вид, частное решение у* может быть найдено методом неопределенных коэффициентов. Метод подбора частного решения у* уравнения Пример: Найдем Отсюда Найдем у*;
8.6 Системы дифференциальных уравнений Для решения многих практических задач в различных областях науки и техники нередко требуется использовать не одну, а много функций. Нахождение этих функций может привести к нескольким ДУ, каждое из которых содержит независимую переменную. Совокупность всех этих ДУ и образует систему. Системой ДУ называется совокупность ДУ каждое из которых содержит независимую переменную, искомые функции и их производные. Общий вид системы ДУ первого порядка, содержащей n искомых функций
Система ДУ первого порядка, разрешенных относительно производной, т.е. система вида
называется нормальной системой ДУ. При этом предполагается, что число уравнений равно числу искомых функций. Замечание: Во многих случаях системы уравнений и уравнения высших порядков можно свести к нормальной системе (1). Так система трех ДУ второго порядка
описывающая движение точки в пространстве, путем введения новых переменных
Подобную операцию можно производить и с системами уравнений, содержащих производные более старшего порядка. Отсюда следует полезность изучения именно нормальных систем. Решением системы (1) называется совокупность из n функций Задача Коши для системы ставится так: найти решение системы уравнений (1) удовлетворяющее начальным условиям (2).Условия существования и единственность решения определяется теоремой Коши. Теорема Коши: Если в системе (1) все функции непрерывны вместе со своими частными производными по Меняя в области Д точку Это решение является общим, если по заданным начальным условиям (2) можно однозначно определить постоянные
Решение, получающееся из общего, при конкретных значениях постоянных (
Одним из основных методов решения нормальной системы ДУ является метод сведения системы к одному ДУ высшего порядка. (Обратная задача – переход от ДУ к системе – рассмотрена ранее) Сам метод основан на следующих соображениях: Пусть задана система нормальных ДУ (1).Продифференцируем по х любое, например, первое уравнение Подставив в это равенство значение производных
Из первых (n-1) уравнений системы (3) выразим функции
Найденные значения
Продифференцировав его (n-1) раз и подставив значения производных
Пример: Решить систему уравнений Продифференцируем первое уравнение: Составим систему уравнений Подставляем z во второе уравнение последней системы:
Получили ЛОДУ второго порядка. Решаем его; характеристическое уравнение имеет вид
Найдем функцию z.Значения Таким образом, общее решение данной системы уравнений имеет вид:
|
||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

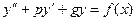 (24)
(24) Общее решение этого уравнения представляет собой сумму общего решения
Общее решение этого уравнения представляет собой сумму общего решения 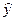 соответствующего однородного уравнения и частного решения у* неоднородного. Частное решение может быть найдено методом вариации произвольных постоянных.
соответствующего однородного уравнения и частного решения у* неоднородного. Частное решение может быть найдено методом вариации произвольных постоянных.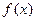 уравнения имеет «специальный вид»:
уравнения имеет «специальный вид»: 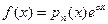 или II.
или II. 
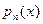 - многочлен степени n.
- многочлен степени n.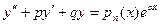 (25)
(25)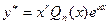 . Здесь r – число равное кратности
. Здесь r – число равное кратности  , как корня характеристического уравнения.
, как корня характеристического уравнения.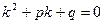 (т.е. r – число, показывающее, сколько раз
(т.е. r – число, показывающее, сколько раз 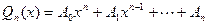 - многочлен степени n, записанный с неопределенными коэффициентами
- многочлен степени n, записанный с неопределенными коэффициентами 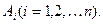
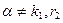 . Следовательно,
. Следовательно,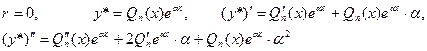
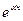 , получим:
, получим: 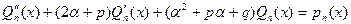 (26)
(26)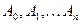 .
.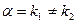 . В этом случае искать решение в форме
. В этом случае искать решение в форме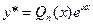 нельзя, т.к.
нельзя, т.к. 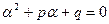 , и уравнение (26)принимает вид
, и уравнение (26)принимает вид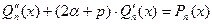 .
.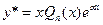 (в частном решении положить (r = 1)).
(в частном решении положить (r = 1)).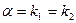 . В этом случае
. В этом случае  , а поэтому уравнение (26) принимает вид
, а поэтому уравнение (26) принимает вид  . Слева стоит многочлен степени n-2. Понятно, что чтобы иметь слева многочлен степени n,частное решение у* следует искать в виде
. Слева стоит многочлен степени n-2. Понятно, что чтобы иметь слева многочлен степени n,частное решение у* следует искать в виде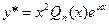 (т.е. в частном решении уравнения надо положить r =2).
(т.е. в частном решении уравнения надо положить r =2).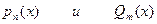 - многочлены степени n и m соответственно,
- многочлены степени n и m соответственно, 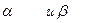 - действительные числа. Уравнение (24) запишется в виде
- действительные числа. Уравнение (24) запишется в виде 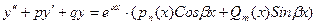 (27)
(27)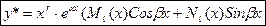 (28), где
(28), где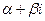 , как корня характеристического уравнения
, как корня характеристического уравнения 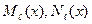 - многочлены степени
- многочлены степени  с неопределенными коэффициентами,
с неопределенными коэффициентами, 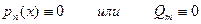 .
.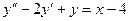
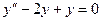 , его характеристическое уравнение
, его характеристическое уравнение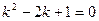 имеет корень
имеет корень  кратности 2. Значит
кратности 2. Значит 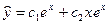 . Находим частное решение исходного уравнения.В нем правая часть
. Находим частное решение исходного уравнения.В нем правая часть 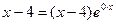 есть формула вида
есть формула вида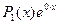 , причем
, причем 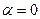 не является корнем характеристического уравнения
не является корнем характеристического уравнения 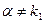 . Поэтому, частное решение ищем как частное решение уравнения (25) в виде
. Поэтому, частное решение ищем как частное решение уравнения (25) в виде 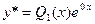 ,т.е.
,т.е. 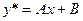 , где A и B – неопределенные коэффициенты.Тогда
, где A и B – неопределенные коэффициенты.Тогда 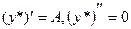 . Подставив
. Подставив 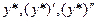 в исходное уравнение получим
в исходное уравнение получим 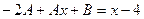 , или
, или 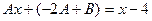 . Приравнивая коэффициенты при одинаковых степенях
. Приравнивая коэффициенты при одинаковых степенях  получаем систему уравнений
получаем систему уравнений 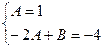 , отсюда А=1,В=-2.
, отсюда А=1,В=-2.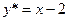 . Следовательно,
. Следовательно,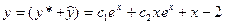 - искомое общее решение уравнения.
- искомое общее решение уравнения.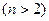 с постоянными коэффициентами и правой специальной частью.
с постоянными коэффициентами и правой специальной частью.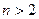 порядка
порядка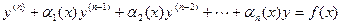 , где
, где 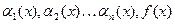 - заданные непрерывные функции на (
- заданные непрерывные функции на ( ,b). Соответствующее ему однородное уравнение имеет вид
,b). Соответствующее ему однородное уравнение имеет вид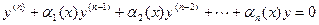
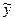 соответствующего ему однородного уравнения т.е.
соответствующего ему однородного уравнения т.е. 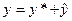 .
.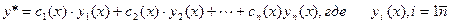 - частные решения, образующие фундаментальную систему однородного уравнения.
- частные решения, образующие фундаментальную систему однородного уравнения.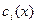 имеет вид
имеет вид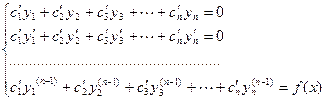
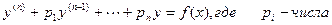 , а правая часть f(x) имеет специальный вид описанный в п.3 для случая n =2, переносится без всякого изменения и на случай уравнения, имеющего порядок
, а правая часть f(x) имеет специальный вид описанный в п.3 для случая n =2, переносится без всякого изменения и на случай уравнения, имеющего порядок 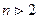 .
.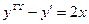
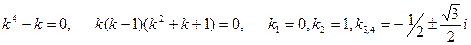
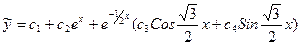
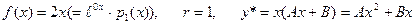 , следовательно
, следовательно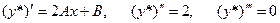 . Тогда
. Тогда 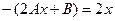 , откуда А= -1,В=0 и получим
, откуда А= -1,В=0 и получим 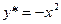 . Следовательно функция
. Следовательно функция 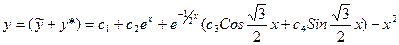 является общим решением уравнения.
является общим решением уравнения.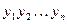 , следующий:
, следующий: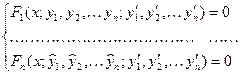
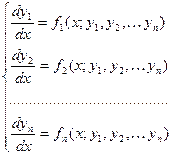 (1)
(1)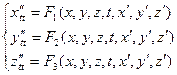
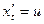 ,
, 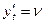 и
и 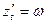 можно привести к нормальной системе ДУ.
можно привести к нормальной системе ДУ.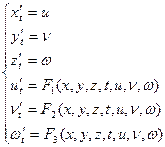
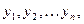 удовлетворяющих каждому из уравнений этой системы. Начальные условия для системы (1) имеют вид
удовлетворяющих каждому из уравнений этой системы. Начальные условия для системы (1) имеют вид 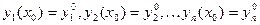 . (2)
. (2) в некоторой области
в некоторой области 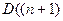 - мерного пространства), то в каждой точке
- мерного пространства), то в каждой точке 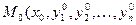 этой области существует, и притом единственное, решение
этой области существует, и притом единственное, решение 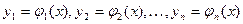 системы, удовлетворяющее начальным условиям (2).
системы, удовлетворяющее начальным условиям (2).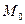 (т.е. начальные условия) получим бесчисленное множество решений, которое можно записать в виде решения зависящего от n произвольных постоянных:
(т.е. начальные условия) получим бесчисленное множество решений, которое можно записать в виде решения зависящего от n произвольных постоянных: 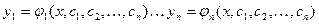
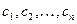 , из системы уравнений
, из системы уравнений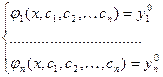

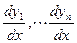 из системы (1) получим
из системы (1) получим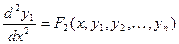 . Продолжая этот процесс (дифференцируем- подставляем- получаем) найдем:
. Продолжая этот процесс (дифференцируем- подставляем- получаем) найдем: 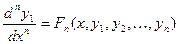 . Соберем все уравнения в систему
. Соберем все уравнения в систему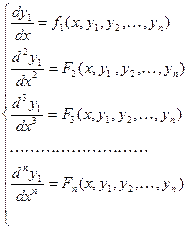 (3)
(3)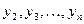 через
через 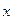 , функцию
, функцию  и ее производные
и ее производные 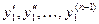 . В результате получим:
. В результате получим: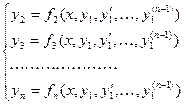 (4)
(4)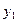 :
: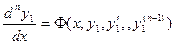 . Пусть его решение есть
. Пусть его решение есть 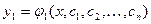 .
.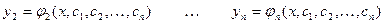 .
.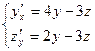
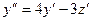 , подставляем
, подставляем 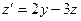 в полученное равенство
в полученное равенство  .
. . Из первого уравнения системы выражаем z через y и
. Из первого уравнения системы выражаем z через y и  :
: 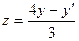 (5)
(5)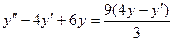 т.е.
т.е. 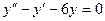
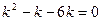 ,
, 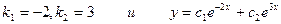 - общее решение уравнения.
- общее решение уравнения.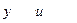
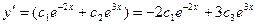 подставим в выражение z через
подставим в выражение z через 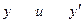 (5).Получим:
(5).Получим: 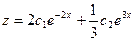 .
.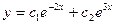 ,
, 


