
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение определенного интегралаСодержание книги
Поиск на нашем сайте
Пусть в нашем распоряжении есть функция
Если при этом интегральная сумма Sn имеет предел равный J, который не зависит от способа разбиения отрезка Теор. Коши. Если функция Непрерывность функции является достаточным условием ее интегрируемости. Однако, неопределенный интеграл может существовать и для некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва.
2)
 задана непрерывная функция задана непрерывная функция  . Нарисуем график этой функции. Фигура ограниченная сверху графиком функции . Нарисуем график этой функции. Фигура ограниченная сверху графиком функции  , снизу осью ox, сбоку линиями x=a и x=b называется криволинейной трапецией. Найдем площадь этой трапеции. Для этого отрезок , снизу осью ox, сбоку линиями x=a и x=b называется криволинейной трапецией. Найдем площадь этой трапеции. Для этого отрезок  разделим точками разделим точками  на n частей и т.д. повторяя то, что мы делали выше, получим на n частей и т.д. повторяя то, что мы делали выше, получим  - будет равна площади ступенчатой фигуры и приближено площади криволинейной трапеции - будет равна площади ступенчатой фигуры и приближено площади криволинейной трапеции
С уменьшением всех величин
Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции. В этом и состоит геометрический смысл определенного интеграла. Работа переменной силы Пусть материальная точка перемещается под действием силы F, направленной вдоль оси OX и имеющей переменную величину
Точность этого равенства возрастает с уменьшением
Формулы Ньютона-Лейбница Пусть Теорема: Если Доказательство: Для этого отрезок Преобразуем каждую разность в скобках по формуле Лагранжа Получим: т.е.
Формула Ньютона-Лейбница позволяет получить удобный способ вычисления определенных интегралов. Чтобы вычислить определенный интеграл от неправильной функции на отрезке Пример:
|
||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.156.91 (0.008 с.) |

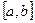 .
. .
. выберем произвольную точку
выберем произвольную точку  и вычислим значение функции в ней, т.е.величину
и вычислим значение функции в ней, т.е.величину 
 и получим величину
и получим величину  .
. .Сумма подобного вида называется интегральной суммой функции
.Сумма подобного вида называется интегральной суммой функции  длину наибольшего частичного отрезка
длину наибольшего частичного отрезка  .
. так, что
так, что  .
. . Таким образом,
. Таким образом,  . Числа
. Числа  и b называются нижними и верхними пределами интегрирования,
и b называются нижними и верхними пределами интегрирования, 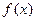 - подынтегральной функцией,
- подынтегральной функцией, 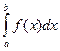 , называется интегрируемой на этом участке.
, называется интегрируемой на этом участке. Геометрический смысл определенного интеграла
Геометрический смысл определенного интеграла
 точность приближения S криволинейной трапеции к S прямоугольной увеличивается. Точность записанного выше соотношения возрастает. Поэтому за точное значение площади криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры Sn, когда
точность приближения S криволинейной трапеции к S прямоугольной увеличивается. Точность записанного выше соотношения возрастает. Поэтому за точное значение площади криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры Sn, когда 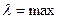 ,
,  .
. , то есть
, то есть  .
. . Найдем работу по перемещению точки М на
. Найдем работу по перемещению точки М на  . Для определения приближенного значения работы на всем участке
. Для определения приближенного значения работы на всем участке  .
.
 .
. - функция, интегрируемая на
- функция, интегрируемая на  - непрерывна на отрезке
- непрерывна на отрезке  ее первообразная на отрезке
ее первообразная на отрезке  ), то имеет место соотношение
), то имеет место соотношение 
 .
. . Рассмотрим соотношение
. Рассмотрим соотношение  .
. .
. ,
,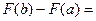
 . Т.к.
. Т.к.  . Получим:
. Получим: .
. значений этой первообразной на концах отрезка
значений этой первообразной на концах отрезка  .
.


