
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые приложения степенных рядовСодержание книги
Поиск на нашем сайте Приближенное вычисление значений функций Пусть требуется вычислить значение функции Для рядов лейбницевского типа
Приближенное вычисление определенных интегралов Бесконечные ряды применяются для вычисления неопределенных и определенных интегралов в случае, когда первообразная не выражается в конечном виде через элементарные функции, либо нахождение первообразной сложно. Пусть требуется вычислить Пример. Вычислить интеграл Решение. Разложим подынтегральную функцию в ряд Макларена, заменяя x на (–x2)
VII Ряды Фурье Основные понятия При изучении процессов, имеющих периодический характер, т.е. процессов, которые через определенный промежуток времени повторяются, более целесообразно разлагать функции, описывающие эти процессы, не в степенной ряд, а в так называемый тригонометрический ряд. Напомним, что функция Для построения графика периодической функции периода T достаточно построить его на любом отрезке длины T и периодически продолжить его на всю область определения. Отметим основные свойства периодической функции: 1) Алгебраическая сумма периодических функций, имеющих один и тот же период T есть периодическая функция с периодом T. 2) Если функция 3) Если функция Доказательство: пусть С другой стороны Но В частности,
Функцию такого вида называют простой гармонической. Основным периодом этой функции является Проведем преобразование этой функции
Отсюда видно, что простое периодическое колебание описывается функциями Сложное гармоническое колебание, возникающее в результате наложения конечного (или бесконечного) числа простых гармоник, также описывается функциями типа Понятно, что при наложении простых гармоник получаем периодическую функцию, описывающую сложное периодическое колебание (периодический процесс). Возникает вопрос: всякую ли периодическую функцию, описывающую периодический процесс, можно представить в виде суммы простых гармоник вида (1) и (2). Если да, то как найти неизвестные параметры каждой из этих гармоник? Ответим сначала на второй, а затем и на первый вопрос.
|
||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 845; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

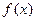 при
при  с заданной точностью
с заданной точностью  . Если функцию
. Если функцию  можно разложить в степенной ряд
можно разложить в степенной ряд 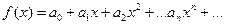 и
и  , то точное значение
, то точное значение 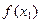 равно сумме этого ряда при
равно сумме этого ряда при 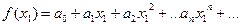 , а приближенное – частичной сумме
, а приближенное – частичной сумме  , т.е.
, т.е.  Точность этого равенства увеличивается с ростом
Точность этого равенства увеличивается с ростом 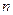 , абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т.е.
, абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т.е. 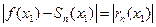 , где
, где  Таким образом, ошибку
Таким образом, ошибку  можно найти, оценив остаток
можно найти, оценив остаток 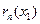 ряда.
ряда. . В остальных случаях (ряд знакопеременный или знакоположительный) составляют ряд из модулей членов ряда и для него стараются найти (подобрать) положительный ряд с большими членами (обычно это сходящийся ряд геометрической прогрессии), который легко бы суммировался. И в качестве оценки
. В остальных случаях (ряд знакопеременный или знакоположительный) составляют ряд из модулей членов ряда и для него стараются найти (подобрать) положительный ряд с большими членами (обычно это сходящийся ряд геометрической прогрессии), который легко бы суммировался. И в качестве оценки  берут величину остатка этого нового ряда.
берут величину остатка этого нового ряда. с точностью до
с точностью до  , то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычисления определяют так же, как и при вычислении значений функции.
, то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычисления определяют так же, как и при вычислении значений функции. с точностью до
с точностью до 

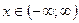 . Интегрируя обе части равенства на отрезке
. Интегрируя обе части равенства на отрезке  , лежащем внутри интервала сходимости
, лежащем внутри интервала сходимости  , получим
, получим  Получили ряд Лейбницевского типа. Так как
Получили ряд Лейбницевского типа. Так как  , а
, а  , то с точностью до 0,001 имеем:
, то с точностью до 0,001 имеем:  .
. , определенная на множестве D, называется периодической с периодом T>0, если при каждом
, определенная на множестве D, называется периодической с периодом T>0, если при каждом  значение
значение  и выполняется равенство
и выполняется равенство  .
. имеет период
имеет период  : действительно,
: действительно,  .
. , то
, то  при любых
при любых  и b
и b 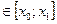 .
. , тогда
, тогда  .
. .
. . Подставляя полученный результат, получим
. Подставляя полученный результат, получим  . Простейшими периодическими функциями являются тригонометрические функции
. Простейшими периодическими функциями являются тригонометрические функции  и
и  . Период этих функций равен 2π, т.е.
. Период этих функций равен 2π, т.е.  . Простейшим периодическим процессом является простое гармоническое колебание, описываемое формулой
. Простейшим периодическим процессом является простое гармоническое колебание, описываемое формулой (1)
(1) , где А – амплитуда колебаний, ω – частота, φ0 – начальная фаза.
, где А – амплитуда колебаний, ω – частота, φ0 – начальная фаза. , т.е. одно полное колебание совершается за промежуток времени
, т.е. одно полное колебание совершается за промежуток времени  (а ω показывает, сколько колебаний совершает точка в течении 2π единиц времени).
(а ω показывает, сколько колебаний совершает точка в течении 2π единиц времени). (2), где
(2), где ,
,  .
. и
и 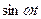 .
. или, что равносильно, функция
или, что равносильно, функция  задает сложное гармоническое колебание. Так как период первой гармонии есть
задает сложное гармоническое колебание. Так как период первой гармонии есть  , второй
, второй  , третьей
, третьей  и т.д., а период функции
и т.д., а период функции  (нулевая гармония) есть любое число, то функция
(нулевая гармония) есть любое число, то функция 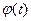 имеет период, равный 2π, т.е.
имеет период, равный 2π, т.е. 


