
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Продуктивные модели ЛеонтьеваСодержание книги
Поиск на нашем сайте
Существует математическая теория исследования и решения уравнения баланса. Не вдаваясь в подробности, остановимся на некоторых основных моментах. Теорема. Если для матрицы А с положительными элементами и вектора Y с положительными компонентами уравнение баланса имеет решение Х с положительными компонентами, то А – продуктивна. Иными словами достаточно установить наличие положительного решения уравнения баланса хотя бы для одного значения вектора Y, чтобы матрица А была продуктивна. Перепишем уравнение баланса с использованием единичной матрицы в виде:
Если существует обратная матрица (Е –А)-1, то существует и единственное решение этого уравнения.
Матрица (Е –А)-1 – называется матрицей полных затрат. Существует несколько критериев продуктивности матрицы А. Один из них говорит, что А продуктивна, если сумма её элементов по любому её столбцу (строк) не превосходит единицы:
Выясним экономический смысл матрицы полных затрат S = (Е –А)-1, для чего зададимся единичными векторами конечного продукта Y1(1,0,0,0…0), Y2(0,1…0),..Yn(0,…1) тогда по (1) соответствующие вектора валового продукта будут:
III. Элементы векторной алгебры Основные понятия Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами являются: длинна, площадь объем, работа, масса. Величины, которые определяются не только своим численным значением, но и направлением называются векторами, пример – скорость, сила. Определение. Направленный отрезок, на котором задано начало, конец и направление называется вектором. Если А и В – начало и конец, то вектор можно обозначить
Расстояние между началом и концом вектора называют его длиной. 1. Векторы 2. Векторы В любой системе координат вектор можно охарактеризовать своими координатами
Длина вектора
Нулевой вектор
Операции над векторами Пусть даны два вектора 1. Сложение. Суммой векторов c1 = a 1+b1, c2= a 2+b2, c3= a 3+b3 . 2. Произведение. Произведение вектора a ≠ 0 на число λ ≠ 0 называется вектор λ Можно показать, что для получения суммы векторов нужно совместить конец вектора
   Геометрический смысл умножения числа на вектор состоит в увеличении его длины в λ раз, при | λ| > 1 или сокращении в λ раз при | λ| < 1. При λ < 0 вектор λ Геометрический смысл умножения числа на вектор состоит в увеличении его длины в λ раз, при | λ| > 1 или сокращении в λ раз при | λ| < 1. При λ < 0 вектор λ  имеет направление противоположное вектору имеет направление противоположное вектору  . Вектора λ . Вектора λ  и коллинеарны. и коллинеарны.
3. Вычитание. Под разностью векторов
Через координаты разность векторов Т.е.
4. Основные свойства линейных операций. 1. 2.( 3. λ ·(α · 4.(α+λ)· 5.λ·( Пусть даны два вектора
5. Скалярное произведение векторов. Скалярным произведением двух векторов
пусть даны (все смешанные произведения = 0).Сопоставляя (1) и (2) получим:
Скалярное произведение векторов обладает следующими свойствами: 1). 2). ( 3). 4). 5). 6. Векторное произведение векторов. Векторным произведением вектора а.) перпендикулярен векторам
с.) Векторы Векторное произведение обозначается Векторное произведение векторов обладает следующими свойствами:
 × ×  )=(λ )=(λ  )× )×  = =  ×(λ ×(λ  ) ) 
 3. 3.  || ||  только тогда, когда только тогда, когда  × ×  = =
 4. ( 4. ( + +  )× )×  = =  × ×  + +  × × 
Векторное произведение можно выразить через координаты:
= Где Это легко доказывается (делать этого не будем). 7. Смешанное произведение векторов.
 × ×  )· )·  - пример смешанного произведения векторов. Здесь - пример смешанного произведения векторов. Здесь  умножается на умножается на  векторно, а затем результат на векторно, а затем результат на  скалярно. Это пример смешанного произведения трех векторов. скалярно. Это пример смешанного произведения трех векторов.
         Для того, чтобы понять смысл этого произведения построим параллелепипед ребрами которого являются Для того, чтобы понять смысл этого произведения построим параллелепипед ребрами которого являются  , ,  , и , и  , а вектор , а вектор
Имеем Где S – площадь параллелограмма, построенного на векторах Свойства смешанного произведения: 1) 2) 3) 4)(axb)c=-(bxa)c и т.д. Выражение смешанного произведения через координаты:
Без доказательства.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 550; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 Матрица А все элементы которой неотрицательны называется продуктивной если для любого вектора Y с неотрицательными компонентами существует решение уравнения баланса причем все элементы вектора Х > 0. В таком случае модель Леонтьева называется продуктивной.
Матрица А все элементы которой неотрицательны называется продуктивной если для любого вектора Y с неотрицательными компонентами существует решение уравнения баланса причем все элементы вектора Х > 0. В таком случае модель Леонтьева называется продуктивной.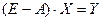
 (1)
(1) и существует номер j, что
и существует номер j, что 
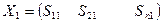 ,
,  ,
, 
 Следовательно, каждый элемент Sij матрицы S есть величина валового выпуска продукции i – отрасли, необходимого для обеспечения выпуска единицы конечного продукта j – ой отросли Yj = 1 (j = 1,n).
Следовательно, каждый элемент Sij матрицы S есть величина валового выпуска продукции i – отрасли, необходимого для обеспечения выпуска единицы конечного продукта j – ой отросли Yj = 1 (j = 1,n). или
или  А B
А B
 (000). Нулевой длины.
(000). Нулевой длины. , координаты которого соответственно равны λ a1, λ a2, λ a3.
, координаты которого соответственно равны λ a1, λ a2, λ a3.

 такой, что
такой, что 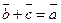 .
.

 и
и  будет равна вектору
будет равна вектору  , причем
, причем  ;
;  ;
;  .
.
 )
) - условие коллинеарности векторов
- условие коллинеарности векторов ·
·  ·cosα (1), где a - угол между
·cosα (1), где a - угол между 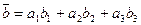 (2)
(2) ;
; +
+ 
 =|
=| 



 b.) имеет длину численно равную площади параллелограмма построенного на векторах
b.) имеет длину численно равную площади параллелограмма построенного на векторах 


 1.
1. 
 =
=
 ,
,  ,
,  – единичные орты, направленные вдоль осей координат
– единичные орты, направленные вдоль осей координат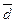

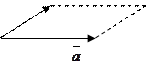
 ,
, – высота параллелепипеда, тогда
– высота параллелепипеда, тогда  .Знак «+» если эти вектора образуют правую тройку и знак «–» если левую, где
.Знак «+» если эти вектора образуют правую тройку и знак «–» если левую, где  - объем параллелепипеда.
- объем параллелепипеда.

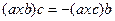
 ;
;


