
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное уравнение первого порядкаСодержание книги
Поиск на нашем сайте
Дифференциальное уравнение первого порядка в общем случае можно записать в виде:
Уравнение связывает независимую переменную х, искомую функцию у и ее производную у’, если это уравнение можно разрешить относительно у’, то его записывают в виде:
Кривая, во всех точках которой направление поля одинаково называется изоклиной. Изоклинами можно пользоваться для приближенного построения интегральных кривых. Уравнение изоклины можно получить, если положить что Д.У. первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме:
где Интегрирование Д.У. в общем случае приводит к бесконечному множеству решений, отличающихся друг от друга на постоянные величины. Чтобы решение Д.У. приобрело конкретный смысл, его надо подчинить некоторым дополнительным условиям. Условие, что при х=х0 функция у должна быть равна заданному числу у0 называется начальным условием. Начальное условие записывается в виде:
Общим решением Д.У. первого порядка называется функция 1) Функция 2) Каково ни было начальное условие, можно найти такое значение постоянной Частым решением Д.У. первого порядка называется любая функция Если общее решение Д.У. найдено в неявном виде, т.е. в виде уравнения С геометрической точки зрения
Задача нахождения решения Д.У. первого порядка, удовлетворяющего заданному начальному условию, называется задачей Коши. Теорема 8.1. Существование и единственность решения задачи Коши. Если в уравнении (2) функция Геометрический смысл теоремы состоит в том, что при выполнении ее условий существует единственная интегральная кривая Д.У., проходящая через точку
1. Уравнения с разделяющимися переменными Наиболее простым Д.У. первого порядка является уравнение вида:
В этом уравнении первое слагаемое зависит от х, а второе от у. Проинтегрировав почленно это уравнение, получим:
Более общий случай описывают уравнения с разделяющимися переменными, которые имеют вид:
Особенности этого уравнения заключаются в том, что коэффициенты при
1) При проведении почленного деления Д.У. на 2) Уравнение 3) Уравнение
Откуда Примеры: 1) Найти общий интеграл уравнения 2)
2. Однородные дифференциальные уравнения
К уравнениям с разделяющимися переменными приводятся однородные Д.У. первого порядка. Функция
Например, функция
Дифференциальное уравнение Покажем, что однородное Д.У. можно записать в виде:
Если
Однородное уравнение (4) преобразуется в уравнение с разделяющимися переменными при помощи замены переменной Действительно, подставив Однородное уравнение часто задается в дифференциальной форме:
Это уравнение будет однородным, если Переписав (5) в виде Пример: Найти общий интеграл уравнения.
Если
3. Линейные уравнения Д.У. первого порядка называется линейным, если его можно записать в виде: Особенность этих Д.У. заключается в том, что искомая функция у и ее производная Рассмотрим два метода решения этих уравнений. (Методы Бернулли и Лагранжа.)
В этом случае решение линейного уравнения ищется в виде произведения двух функций, т.е. с помощью подстановки Тогда Подберем функцию 2. Метод Лагранжа Линейное уравнение решается следующим образом. Рассмотрим соответствующее уравнение без правой части, т.е. уравнение Метод Лагранжа состоит в том, что постоянную с в полученном решении заменяем функцией с(х), т.е. полагаем с=с(х). Решение линейного уравнения при этом ищем в виде:
Найдем производную от этого соотношения.
Второе и третье слагаемые взаимно уничтожаются и окончательно получим:
Подставляя выражение с(х) в (7) получим общее решение линейного Д.У. В заключении отметим, что зачастую метод Лагранжа называют методом вариации произвольной постоянной, что обусловлено тем, что при решении полагают с=с(х).
|
|||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.43.204 (0.008 с.) |

 (1)
(1) (2) и называют Д.У. первого порядка, разрешенным относительно производной. Последнее уравнение устанавливает связь между координатами точки
(2) и называют Д.У. первого порядка, разрешенным относительно производной. Последнее уравнение устанавливает связь между координатами точки  и угловым коэффициентом у - касательной к интегральной кривой, проходящей через эту точку. Следовательно, Д.У.
и угловым коэффициентом у - касательной к интегральной кривой, проходящей через эту точку. Следовательно, Д.У. 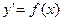 даст совокупность направлений (поле направлений) на плоскости ОХУ. Таково геометрическое истолкование Д.У. первого порядка.
даст совокупность направлений (поле направлений) на плоскости ОХУ. Таково геометрическое истолкование Д.У. первого порядка. , т.е.
, т.е. 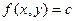 .
.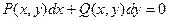
 и
и  – известные функции. Последнее уравнение удобно тем, что переменные х и у в нем равноправны, т.е. любую из них можно рассматривать как функцию другой.
– известные функции. Последнее уравнение удобно тем, что переменные х и у в нем равноправны, т.е. любую из них можно рассматривать как функцию другой.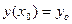 или
или 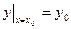
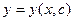 , содержащая одну произвольную постоянную и удовлетворяющая условиям:
, содержащая одну произвольную постоянную и удовлетворяющая условиям: является решением Д.У. при каждом фиксированном значении
является решением Д.У. при каждом фиксированном значении  .
. , что функция
, что функция  удовлетворяет данному начальному условию.
удовлетворяет данному начальному условию.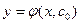 , полученная из общего решения
, полученная из общего решения  при конкретном значении постоянной
при конкретном значении постоянной  , то такое уравнение называется общим интегралом Д.У. Уравнение
, то такое уравнение называется общим интегралом Д.У. Уравнение  есть семейство интегральных кривых на плоскости ХОУ, а частное решение
есть семейство интегральных кривых на плоскости ХОУ, а частное решение  .
. и ее частная производная
и ее частная производная  непрерывны в некоторой области
непрерывны в некоторой области  , содержащей точку
, содержащей точку  этого уравнения, удовлетворяющее начальным условиям.
этого уравнения, удовлетворяющее начальным условиям. (3)
(3) - это общий интеграл.
- это общий интеграл. (4)
(4) и
и  представляют собой произведения двух функций, одна из которых зависит только от х, а другая от у. Уравнение (4) легко сводится к уравнению (3) путем почленного деления его на
представляют собой произведения двух функций, одна из которых зависит только от х, а другая от у. Уравнение (4) легко сводится к уравнению (3) путем почленного деления его на 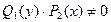 . При этом получим:
. При этом получим: - общий интеграл.
- общий интеграл.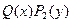 могут быть потеряны некоторые решения. Поэтому следует отдельно решить уравнение
могут быть потеряны некоторые решения. Поэтому следует отдельно решить уравнение  и установить те решения Д.У., которые не могут быть получены из общего решения, так называемые – особые решения.
и установить те решения Д.У., которые не могут быть получены из общего решения, так называемые – особые решения. также сводится к уравнениям, разделяющимися переменными. Для этого достаточно положить
также сводится к уравнениям, разделяющимися переменными. Для этого достаточно положить  и разделить переменные.
и разделить переменные.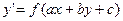 , где
, где 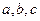 – числа, путем замены
– числа, путем замены  сводится к Д.У. с разделяющимися переменными. Дифференцируя по х, получим:
сводится к Д.У. с разделяющимися переменными. Дифференцируя по х, получим: , т.е.
, т.е. 
 – интегрируя это уравнение и заменяя
– интегрируя это уравнение и заменяя  на
на 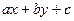 , получим общий интеграл исходного уравнения.
, получим общий интеграл исходного уравнения. . Интегрируя, получим
. Интегрируя, получим  или
или  . Обозначив
. Обозначив  , получим
, получим  – общий интеграл Д.У.
– общий интеграл Д.У. , преобразуем левую часть.
, преобразуем левую часть.  . Делим на
. Делим на  , получим
, получим  . Интегрируя, получим окончательно
. Интегрируя, получим окончательно  или
или  . Поскольку
. Поскольку  является особыми решениями и не входят в общий интеграл.
является особыми решениями и не входят в общий интеграл. , вся функция умножается на
, вся функция умножается на  , т.е.
, т.е. .
. есть однородная функция второго порядка, поскольку
есть однородная функция второго порядка, поскольку .
.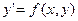 называется однородным, если функция
называется однородным, если функция  (4)
(4) . Положив
. Положив 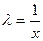 получим:
получим:
 или, что то же самое
или, что то же самое  .
. в уравнение (4), получаем
в уравнение (4), получаем  или
или  , т.е. уравнение с разделяющимися переменными. Найдя его общее решение следует заменить в нем
, т.е. уравнение с разделяющимися переменными. Найдя его общее решение следует заменить в нем 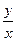 . Получим общее решение исходного уравнения.
. Получим общее решение исходного уравнения.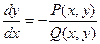 и применив в правой части рассмотренное выше преобразование, получим уравнение
и применив в правой части рассмотренное выше преобразование, получим уравнение  . При интегрировании уравнений (5) нет необходимости предварительно приводить их к виду (4). Подстановка
. При интегрировании уравнений (5) нет необходимости предварительно приводить их к виду (4). Подстановка 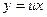 сразу преобразует уравнение (5) в уравнение с разделяющимися переменными.
сразу преобразует уравнение (5) в уравнение с разделяющимися переменными.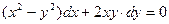 - это однородное уравнение. Положим
- это однородное уравнение. Положим  , тогда
, тогда  и получим
и получим  , или после преобразований:
, или после преобразований:  - это уравнение с разделяющимися переменными. Делим переменные
- это уравнение с разделяющимися переменными. Делим переменные  после интегрирования получим
после интегрирования получим  или
или  .
. , то
, то  , переходя к старым неизвестным, получим
, переходя к старым неизвестным, получим  – решение исходного уравнения.
– решение исходного уравнения. , где
, где  – заданные функции и в частности постоянные.
– заданные функции и в частности постоянные. входят в уравнение первой степени не перемножаясь между собой.
входят в уравнение первой степени не перемножаясь между собой. , где
, где 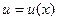 и
и  – неизвестные функции от х, причем одна из них произвольная. Так любую у(х) можно записать в виде
– неизвестные функции от х, причем одна из них произвольная. Так любую у(х) можно записать в виде  .
.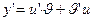 . Делая подстановку в линейном Д.У. получим
. Делая подстановку в линейном Д.У. получим  или
или  (6).
(6).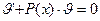 . Итак,
. Итак,  т.е.
т.е. 
 или
или  . Ввиду свободы выбора функции
. Ввиду свободы выбора функции  можно принять с=1, тогда
можно принять с=1, тогда 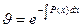 . Подставляя найденное значение в (6), получим
. Подставляя найденное значение в (6), получим  . Это уравнение с разделяющимися переменными. Решаем его.
. Это уравнение с разделяющимися переменными. Решаем его.  .Интегрируя получим:
.Интегрируя получим:  . Возвращаясь к переменной у, получим окончательно
. Возвращаясь к переменной у, получим окончательно  . Это решение исходного линейного Д.У.
. Это решение исходного линейного Д.У.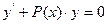 . Оно называется линейным однородным Д.У. первого порядка. В этом уравнении можно провести разделение переменных.
. Оно называется линейным однородным Д.У. первого порядка. В этом уравнении можно провести разделение переменных.  и
и 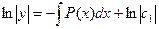 .Таким образом,
.Таким образом, 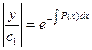 , т.е.
, т.е.  или
или  , где
, где 
 (7)
(7) Подставляем значения у и у’ в линейное уравнение
Подставляем значения у и у’ в линейное уравнение 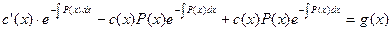 .
. . Следовательно,
. Следовательно,  . Интегрируя, получим:
. Интегрируя, получим:  .
.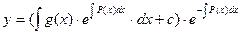 , что совпадает с результатом полученным методом Бернулли.
, что совпадает с результатом полученным методом Бернулли.


