
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенное вычисление определенного интегралаСодержание книги
Поиск на нашем сайте
Пусть требуется найти определенный интеграл
Формулы прямоугольников
 Пусть на отрезке Пусть на отрезке  задана непрерывная функция задана непрерывная функция 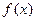 . Требуется вычислить . Требуется вычислить  интеграл интеграл  численно равный площади соответствующей трапеции. Разобьем основание этой трапеции, т.е. отрезок численно равный площади соответствующей трапеции. Разобьем основание этой трапеции, т.е. отрезок 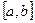 на на 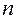 равных частей длины равных частей длины  с помощью точек с помощью точек  . Можно записать, что . Можно записать, что 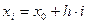 . В середине каждого отрезка . В середине каждого отрезка  . Построим ординату . Построим ординату  графика функции графика функции  (Рис.9.). Приняв эту ординату за высоту, построим прямоугольник с площадью (Рис.9.). Приняв эту ординату за высоту, построим прямоугольник с площадью  . Тогда сумма площадей всех прямоугольников даст площадь фигуры, представляющую собой приближенное значение искомого определенного интеграла: . Тогда сумма площадей всех прямоугольников даст площадь фигуры, представляющую собой приближенное значение искомого определенного интеграла:  . Эта формула и называется формулой прямоугольников. Абсолютная погрешность оценивается с помощью следующего соотношения . Эта формула и называется формулой прямоугольников. Абсолютная погрешность оценивается с помощью следующего соотношения  , где , где  - максимальное значение - максимальное значение  на отрезке на отрезке 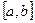 . .
Формула трапеций Эту формулу получают аналогично формуле прямоугольников. Только на каждом частичном отрезке криволинейная трапеция заменяется обычной. Разобьем отрезок
8.3. Формула парабол (Симпсона) Если заменить график функции Выводить мы ее не будем, а ограничимся записью конечного выражения:
Абсолютная погрешность оценивается соотношением
Кратные интегралы Двойной интеграл. Основные понятия Обобщением определенного интеграла на случай функции двух переменных является так называемый двойной интеграл.
х, у – переменные интегрирования, dxdy (или dS) элемент площади. Для всякой ли функции существует двойной интеграл? Ответ дает следующая теорема: Теорема. (Достаточное условие интегрируемости функции) Если функция Далее мы будем рассматривать только непрерывные функции, хотя двойной интеграл может существовать не только для непрерывных функций.
|
||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.205.114 (0.005 с.) |

 функции
функции  . Но поиск первообразной функции иногда весьма сложен, кроме того не для всякой функции первообразная выражается через элементарные функции. В этих и других случаях прибегают к приближенным формулам, с помощью которых интеграл находится с любой степенью сложности.
. Но поиск первообразной функции иногда весьма сложен, кроме того не для всякой функции первообразная выражается через элементарные функции. В этих и других случаях прибегают к приближенным формулам, с помощью которых интеграл находится с любой степенью сложности. . Абсциссы точек деления
. Абсциссы точек деления  соответствующие им ординаты графика функции, тогда расчетные формулы для этих значений примут вид:
соответствующие им ординаты графика функции, тогда расчетные формулы для этих значений примут вид:  ,
, 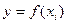 . Заменим кривую
. Заменим кривую  и
и  . Тогда площадь криволинейной трапеции с основанием
. Тогда площадь криволинейной трапеции с основанием  или
или  - это формула трапеций. Абсолютная погрешность
- это формула трапеций. Абсолютная погрешность  приближения, полученного по формуле трапеций, оценивается с помощью формулы:
приближения, полученного по формуле трапеций, оценивается с помощью формулы: , где
, где  при
при  .
. на каждом отрезке
на каждом отрезке  не отрезками прямых, как в случае формулы трапеции, а дугами парабол, то получим более точную формулу вычисления интеграла
не отрезками прямых, как в случае формулы трапеции, а дугами парабол, то получим более точную формулу вычисления интеграла  - это так называемая формула Симпсона.
- это так называемая формула Симпсона. , где
, где  - максимальное значение
- максимальное значение 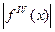 при
при  Пусть в замкнутой области
Пусть в замкнутой области  плоскости XOY задана непрерывная функция
плоскости XOY задана непрерывная функция  . Разобьем область
. Разобьем область 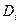 (рис.1), площади которых обозначим через
(рис.1), площади которых обозначим через  , а диаметры (наибольшие расстояния между точками области) – через
, а диаметры (наибольшие расстояния между точками области) – через  . В каждой области
. В каждой области  , умножим значение
, умножим значение 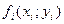 функции в этой точке на
функции в этой точке на  . Эта сумма называется интегральной суммой
. Эта сумма называется интегральной суммой  в области
в области  . Если этот предел существует и не зависит ни от способа разбиения области
. Если этот предел существует и не зависит ни от способа разбиения области  или
или  . Таким образом двойной интеграл определяется равенством
. Таким образом двойной интеграл определяется равенством  . В этом случае функция
. В этом случае функция 


