
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приложения двойного интегралаСодержание книги
Поиск на нашем сайте
Приведем некоторые примеры применения двойного интеграла. 1) Объем тела Как уже говорилось, объем цилиндрического тела можно найти по формуле 2) Площадь плоской фигуры Если положить в формуле для объема тела через двойной интеграл 3) Масса плоской фигуры Пусть дана плоская пластина Разобьем пластину на элементарные части Статические моменты и центр тяжести плоской фигуры Статические моменты могут быть вычислены с использованием раннее полученных соотношений по следующим формулам:
Тройной интеграл. Основные понятия Обобщением определенного интеграла на случай функции трех переменных является так называемый тройной интеграл. Теория тройного интеграла аналогична теории двойного интеграла, поэтому изложим ее в сокращенном виде. Пусть в замкнутой области V пространства OXYZ задана непрерывная функция Теорема. Если функция Тройной интеграл обладает теми же свойствами, что и двойной: 1) 2) 3) 4) 5) 6) Оценка тройного интеграла
7) Теорема о среднем значении Если функция
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 392; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.78.185 (0.006 с.) |

 , где
, где  - уравнение поверхности, ограничивающей тело сверху.
- уравнение поверхности, ограничивающей тело сверху. =1, то цилиндрическое тело превратить в прямой цилиндр с высотой Н=1. Объем такого цилиндра численно равен, как известно, площади S основания
=1, то цилиндрическое тело превратить в прямой цилиндр с высотой Н=1. Объем такого цилиндра численно равен, как известно, площади S основания  . При этом получится формула для вычисления площади S области
. При этом получится формула для вычисления площади S области  .
. .
.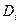 , площади которых обозначим через
, площади которых обозначим через  . В каждой области
. В каждой области  . Если область
. Если область 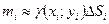 , а так как масса всей пластины
, а так как масса всей пластины  , то можно записать
, то можно записать  . Точное значение m получим, как предел этой суммы при
. Точное значение m получим, как предел этой суммы при  и
и 
 , т.е.
, т.е.  .
. и
и  , а координаты центра масс фигуры по формулам:
, а координаты центра масс фигуры по формулам:  и
и  .
. . Разбив область V сеткой поверхностей на n частей
. Разбив область V сеткой поверхностей на n частей  и выбрав в каждой их них произвольную точку
и выбрав в каждой их них произвольную точку  составим интегральную сумму
составим интегральную сумму  для функции
для функции  по области V (∆Vi – объем элементарной области Vi). Если предел интегральной суммы существует при неограниченном увеличении числа n таким образом, что каждая Vi стягивается в точку, то его называют тройным интегралом от функции
по области V (∆Vi – объем элементарной области Vi). Если предел интегральной суммы существует при неограниченном увеличении числа n таким образом, что каждая Vi стягивается в точку, то его называют тройным интегралом от функции  (или
(или  ). Таким образом, по определению получаем
). Таким образом, по определению получаем  . Здесь
. Здесь  - элемент объема
- элемент объема  - диаметр i-области.
- диаметр i-области. , где
, где  .
. .
. , если
, если  , а пересечение V1 и V2 состоит из границы, их разделяющей.
, а пересечение V1 и V2 состоит из границы, их разделяющей. , если в V,
, если в V,  . Если же в V,
. Если же в V, 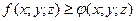 , то и
, то и  .
. , так как в случае
, так как в случае  любая интегральная сумма имеет вид
любая интегральная сумма имеет вид  и численно равна объему тела.
и численно равна объему тела. , где m и M – соответственно наименьшее и наибольшее значение функции
, где m и M – соответственно наименьшее и наибольшее значение функции  , что
, что  , где V – объем тела.
, где V – объем тела.


