
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные дифференциальные уравнения высших порядков.Содержание книги
Поиск на нашем сайте
Уравнение вида заданные функции (от Оно содержит искомую функцию Разделив уравнение на можно записать уравнение в виде приведенного уравнения
В дальнейшем будем рассматривать уравнения типа (10) считая, что свободный член и коэффициенты являются непрерывными функциями (на некотором интервале
1. Линейные однородные ДУ второго порядка Рассмотрим линейное однородное дифференциальное уравнение (ЛОДУ) второго порядка Теорема 3 Если функции
Из теоремы вытекает, что если Функции
выполняется тогда и только тогда, когда Например, функции Оказывается, что совокупность любых двух линейно независимых на интервале Теперь можно сформулировать при каких условиях только что приведенная комбинация будет общим решением уравнения (11). Теорема 4( Структура общего решения ЛОДУ второго порядка) Если два частных решения где
Согласно теореме 3 функция (12) является решением уравнения (11).Поэтому остается доказать, что это решение общее, т.е. что из него можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям
Это легко можно доказать, но мы этого делать не будем.
2. Линейные однородные ДУ n- го порядка. Полученные выше результаты можно распространить на линейные однородные дифференциальные уравнения n-го порядка, имеющие вид
1. Если функция
2. Функции линейно зависимы.
3. Частные решения
4. Общее решение ЛОДУ(13) имеет вид
|
||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 579; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 где
где  -
- ) называют линейным ДУ n-го порядка.
) называют линейным ДУ n-го порядка. и все ее производные лишь в первой степени. Функции
и все ее производные лишь в первой степени. Функции  называются коэффициентами уравнения, а
называются коэффициентами уравнения, а  - его свободным членом.Если
- его свободным членом.Если  то уравнение называется однородным линейным дифференциальным уравнением. Если
то уравнение называется однородным линейным дифференциальным уравнением. Если  , то уравнение называется неоднородным.
, то уравнение называется неоднородным. и обозначив
и обозначив 
 (10)
(10) .
. (11)
(11) и
и  являются частными решениями уравнения (11), то решением этого уравнения является также функция
являются частными решениями уравнения (11), то решением этого уравнения является также функция  , где
, где  и
и  произвольные постоянные.
произвольные постоянные. и
и  - решения уравнения (11),то решениями этого уравнения будут также функции
- решения уравнения (11),то решениями этого уравнения будут также функции 
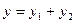 и
и  . Решение содержит две постоянные величины
. Решение содержит две постоянные величины  и
и 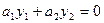 (12)
(12) .Если хотя бы одно из чисел
.Если хотя бы одно из чисел  или
или  отличны от нуля и равенство (12) выполняется,то функции
отличны от нуля и равенство (12) выполняется,то функции  .Очевидно, что функции
.Очевидно, что функции  выполняется равенство
выполняется равенство  или
или  , где
, где  .
. и
и  линейно зависимы, т.к.
линейно зависимы, т.к.  а
а  линейно независимы т.к.
линейно независимы т.к.  .
. и
и  ЛОДУ второго порядка определяет фундаментальную систему решений этого уравнения: любое произвольное решение может быть получено как комбинация
ЛОДУ второго порядка определяет фундаментальную систему решений этого уравнения: любое произвольное решение может быть получено как комбинация  .
. (12)
(12)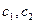 - произвольные const.
- произвольные const. где
где  .
. (13)
(13) является частным решением уравнения (13), то его решением является и функция
является частным решением уравнения (13), то его решением является и функция  .
. называются линейно независимыми на
называются линейно независимыми на  выполняется лишь в случае, когда все числа
выполняется лишь в случае, когда все числа  , в противном случае (если хотя бы одно из чисел
, в противном случае (если хотя бы одно из чисел  не равно нулю) функции
не равно нулю) функции  - произвольные постоянные,
- произвольные постоянные,  - частные решения уравнения (13), образующие фундаментальную систему.
- частные решения уравнения (13), образующие фундаментальную систему.


