
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множества. Действительные числаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Понятие множества является одним из основных неопределяемых понятий в математике. Под множеством понимают совокупность некоторых объектов, объединенных по определенному признаку. Объекты, составляющие множество называются его элементами (точками). Множество принято обозначать заглавными буквами латинского алфавита (A,B...X,Y), а элементы малыми ( Множество, не содержащее ни одного элемента, называют пустыми (ø). Элементы множеств записывают в фигурных скобках, внутри которых они перечислены. Например, запись А={1,5,10}означает, что множество А состоит из трех чисел 1,5 и 10. Введем понятие суммы множеств. Суммой множеств X иY называется совокупность элементов, принадлежащих X и Y. Сумма этих множеств обозначается X U Y. Произведение (пересечение) множеств X и Y является совокупность элементов принадлежащих множеству Х и Y одновременно. Пересечение обозначают X ∩Y. Множества, элементами которого являются числа, называют числовыми. Пример:
и R-множество действительных чисел- содержит рациональные и иррациональные числа. Рациональные - выражаются или конечной десятичной дробью или бесконечной периодической дробью. Действительные числа не являющиеся рациональными называются иррациональными. 2. Числовые последовательности Числовые последовательности представляют собой бесконечные множества чисел. Под числовой последовательностью x1,x2.....xn понимают совокупность чисел из натурального ряда 1) последовательность 2) последовательность аналогичным образом определяется убывающая последовательность Все эти последовательности называются монотонными последовательностями. 3) последовательность 4) последовательность Основные свойства бесконечно малых последовательностей: 1) сумма и разность двух бесконечно малых последовательностей является бесконечно малыми последовательностями. Пусть возьмем N=max(N1,N2), тогда при n>N одновременно должны выполняться два неравенства
Значит при всех n>N Тогда в соответствии с определением последовательности 2)произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность; 3) произведение бесконечно малой последовательности на ограниченную последовательность является бесконечно малой последовательностью. Последние два свойства примем без доказательств. 3. Сходящиеся последовательности. Предел числовой последовательности Число
Последовательность, имеющая предел, называется сходящейся. Если предел последовательности равен числу
Или
Последовательность, не имеющая предела, называется расходящейся. Полученное неравенство равносильно неравенствам:
Или
Поэтому определение предела последовательности геометрически можно сформулировать так: число Отсюда следует, что сходящаяся последовательность имеет только один предел. Свойства сходящихся последовательностей. 1) если все элементы бесконечно малой последовательности Доказательство: пусть с≠0 возьмем 2)Сходящая последовательность ограничена; 3) сумма (разность) сходящихся последовательностей 4) произведение сходящих последовательностей 5) частное двух сходящихся последовательностей Все эти свойства необходимы для определения пределов различных последовательностей. Доказывать все не будем. Рассмотрим лишь в качестве примера доказательство свойства 3. Доказательство: пусть a и b – соответственно пределы 4. Признак сходимости монотонные последовательности Монотонные последовательности классифицируются по соотношению между соседними элементами, о чем говорилось выше. Монотонные последовательности ограничены либо сверху (убывающие), либо снизу (возрастающие). Сформулируем признак существования предела таких последовательностей (теорема Вейерштрасса). Теорема: В сякая монотонная ограниченная последовательность имеет предел. В качестве примера рассмотрим последовательность:
Полагая
Или
Отсюда следует, что с увеличением n, число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n, число
усилим полученное неравенство, заменив числа 3,4,5….n, стоящие в знаменателях дробей на 2n-1.
Сумма в скобках - сумма членов геометрической прогрессии:
Поэтому Следовательно, по теореме Вейерштрасса, последовательность Следовательно:
Число е играет большую роль, в математике и является иррациональным (число Эйлера, Неперово число). Рассмотрим задачу о непрерывном начислении % Пример: первоначальный вклад в банк составил Q0. Банк выплачивает P% годовых. Необходимо найти размер вклада Qt через t- лет. а) при использовании простых процентов. Размер вклада ежегодно будет увеличиваться на одну и ту же величину Будем полагать, что проценты по вкладу начисляются: каждое полугодие (n=2), ежеквартально (n=4), ежемесячно (n=12), каждый день (n=365) и т.д. Непрерывно (n→∞), тогда размер вклада за t лет составит:
Эта формула показывает показательный (экспоненциальный) закон роста (при p>0) или убывания (при p<0). Она может быть использована и при непрерывном начислении процентов.
5. Функции одной переменной Пусть X и Y- некоторые числовые множества и пусть каждому x є X, по какому-либо закону f поставлен в соответствие один элемент y є Y, тогда будем говорить, что определена функциональная зависимость y от x по закону y=f(x). При этом x- называют независимой переменной (аргументом), y – зависимой переменной. Множество X – областью определения (существования), множество Y- областью значений (изменений) функции. Совокупность точек координатной плоскости XOY, удовлетворяющих уравнению y=f(x) называется графиком этой функции. Для обозначения функций могут быть использованы и другие буквы, например:
1) Cпособы задания функций Задать функцию - значит указать закон, по которому каждому значению аргумента из области определения ставится в соответствие (вычисляется) значение зависимой переменной из области значения функции. Существуют три основных способа задания функции: табличный, аналитический и графический. Табличный способ. Этот способ имеет широкое примение в различных отраслях знаний и экспериментальных исследованиях. В этом случае вся цифровая информация заносится в таблицы. Как правило одну из переменных, например, время можно принять за независимую, тогда другие величины будут функциями от этого аргумента. По сути базы данных основан на табличном способе задания Аналитический способ. Этот способ состоит в задании связи между аргументом и функцией в виде аналитического выражения(формул). Следует отметить, что функция может определиться и набором формул. Например:
Графический способ. Здесь соответствие между аргументом и функцией задается посредствам графика. Этот способ широко используется в экспериментальных измерениях с употреблением самопишущих приборов. 2) Область определения функции. В том случае, когда функция задана аналитически y=f(x) и никаких ограничений или оговорок не имеется, область ее определения находится по соблюдению законности выполнения математических операций, входящих в формулу f. Эти ограничения известны: подкоренное выражение в корне четной степени не может быть <0. знаменатель дроби не может быть=0 и т.п. Пример № 1: Область определения функции Пример № 2: Или Пример- зависимость удлинения металлического стержня от температуры ∆l=α∆T и ограничение температурой плавления тела. 3) Свойства функций Рассмотрим основные свойства функций: 1. четность и нечетность. Функция y=f(x) – четная, если для любых значений x из области определения f(-x)=f(x) и нечетной f(-x)=-f(x). Примеры: y=x- нечетная функция, y=x2 - четная. 2. монотонность. Функция f=f(x) называется возрастающей (убывающей) на промежутке X, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции. Функции, возрастающие и убывающие, называются монотонными. 3. ограниченность. Функция f(x) называется ограниченной на промежутке X, если существует такое положительное число M>0, что |f(x)|≤M для любого x є X. В противном случае функция называется неограниченной. 4. периодичность. Функция y=f(x) называется периодической с периодом T≠0, если для любых x из области определения f(x+T)=f(x). Пример: y=Sinx, T=2 5. обратная функция. Пусть y=f(x) есть функция от независимой переменной x определенной на множестве X с областью значений Y. Поставим в соответствие каждому yєY единственное значение x є X, при котором f(x)=y. Тогда полученная функция x= 6. сложная функция. Пусть функция y=f(u) есть функция от переменной u определенной на множестве U, с областью значений Y, а переменная u, в свою очередь, является функцией u= 7. явная и неявная функции. Функция называется явной если она задана формулой, в которой правая часть не содержит зависимой переменной. Например: 4) Понятие элементарной функции К основным элементарным функциям относят: 1. показательная функция y= 2. степенная функция y= 3. логарифмическая функция y= 4. тригонометрические функции y=Sinx, y=Cosx, y=tgx и y=ctgx Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных, с помощью конечного числа арифметических операций и операций взятия функции от функции, называется элементарной функцией. 5) Применение функций в экономике Функции находят широкое применение в экономической теории и практике. Спектр используемых в экономике функций достаточно широк: от простейших линейных до функций, получаемых по определенному алгоритму с помощью так называемых реккурентных соотношений, связывающих состояние изучаемых объектов в различные периоды времени. Наиболее часто в экономике используются следующие функции: 1. функция полезности- в широком смысле зависимость полезности, т.е. результата, эффекта некоторого действия, от уровня действия; 2. производственная функция- зависимость результата производственной деятельности от обуславливающих его факторов 3. функция выпуска- зависимость объема производства от наличия или потребления ресурсов 4. функция издержек- зависимость издержек производства от объема продукции 5. функция спроса-, потребления и предложения- зависимость объема спроса, потребления или предложения на отдельные товары или услуги от различных факторов (например, цены, дохода и т.п.). Учитывая, что экономические явления и процессы обуславливаются действием различных факторов, для их исследования широко используются функции нескольких переменных. Среди этих функций можно выделить мультипликативные функции, позволяющие представить зависимую переменную в виде произведения факторных переменных, обращающих его в ноль при отсутствии действия хотя бы одного фактора.
Предел функции Предел функции в точке Пусть функция y=f(x) определена в некоторой окрестности точки x0, кроме, самой точки. Число A называется пределом функции в точке x0(или при x→ x0), если для любого положительного Это определение означает, что функция f(x) имеет предел в точке x0, если для любой

        Число A1(A2) называется правым (левым) пределом функции в точке x0, если для любого Число A1(A2) называется правым (левым) пределом функции в точке x0, если для любого  >0 существует такое >0 существует такое  >0, что для всех x из правой (левой) >0, что для всех x из правой (левой)  - окрестности точки x0 т.е. - окрестности точки x0 т.е.  , выполняется неравенство , выполняется неравенство  ; ;  . Записывается . Записывается
Рис.1 или f(x0-0)=A2
Пределы функции справа и слева называются односторонним пределами. Очевидно, если существует 2) Предел функции при x→∞.
  Пусть y=f(x) определена в промежутке (−∞;∞). Число A называется пределом функции f(x) при x→∞, если для любого Пусть y=f(x) определена в промежутке (−∞;∞). Число A называется пределом функции f(x) при x→∞, если для любого  >0 существует такое число M, что при всех |x|>M справедливо неравенство >0 существует такое число M, что при всех |x|>M справедливо неравенство  . Этот предел записывается . Этот предел записывается  . .
     Геометрический смысл – соответствующие значения функции f(x) попадают в Геометрический смысл – соответствующие значения функции f(x) попадают в  – окрестности точки A, т.е. точки графика лежат в полосе шириной 2 – окрестности точки A, т.е. точки графика лежат в полосе шириной 2  ограниченной прямыми y=A- ограниченной прямыми y=A-  и y=A+ и y=A+  (Рис.2). (Рис.2).
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 761; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |

 ,b....x,y). Если элемент принадлежит множеству X, то пишут x є X.
,b....x,y). Если элемент принадлежит множеству X, то пишут x є X. -множество натуральных чисел
-множество натуральных чисел -множество целых неотрицательных чисел
-множество целых неотрицательных чисел -множество целых чисел
-множество целых чисел -множество рациональных чисел
-множество рациональных чисел ,
,  .....
.....  каждое из которых поставлено в соответствии вещественному числу
каждое из которых поставлено в соответствии вещественному числу  . Числа
. Числа  ,
,  ....
....  называется ограниченной если существует такое число A>0, что для любого n є N выполняется неравенство
называется ограниченной если существует такое число A>0, что для любого n є N выполняется неравенство  . В противном случае последовательность- неограниченна.
. В противном случае последовательность- неограниченна.

 называется бесконечно малой, если для положительного
называется бесконечно малой, если для положительного  существует такой номер N, что при n>N выполняется равенство |αn|<
существует такой номер N, что при n>N выполняется равенство |αn|<  - бесконечно малые последовательности. Докажем, что
- бесконечно малые последовательности. Докажем, что  - бесконечно малая. Пусть
- бесконечно малая. Пусть  , а N2 – номер начиная с которого
, а N2 – номер начиная с которого  . Такие номера должны найтись в соответствии с определением б.м.п.
. Такие номера должны найтись в соответствии с определением б.м.п.


 , то это записывается так:
, то это записывается так:
 при
при 



 . По определению бесконечно малой последовательности существует такой N, что при n>N выполняется неравенство |xn|<
. По определению бесконечно малой последовательности существует такой N, что при n>N выполняется неравенство |xn|<  , а это верно только при c=0 ч.т.д.
, а это верно только при c=0 ч.т.д. есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательности;
есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательности; есть сходящаяся последовательность, предел которой равен частному пределов последовательностей
есть сходящаяся последовательность, предел которой равен частному пределов последовательностей  где
где  , отсюда получим:
, отсюда получим:  . поскольку,
. поскольку,  тоже величина бесконечно малая, откуда и следует, что число (а±b) является пределом сходящейся последовательности. ч.т.д.
тоже величина бесконечно малая, откуда и следует, что число (а±b) является пределом сходящейся последовательности. ч.т.д. ,
,  .По формуле бинома Ньютона:
.По формуле бинома Ньютона:

 bn
bn получим:
получим:
 =
=


 убывает, поэтому величины
убывает, поэтому величины  ... возрастают. Поэтому последовательность
... возрастают. Поэтому последовательность 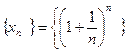 - возрастающая. При этом
- возрастающая. При этом  . Покажем, что эта последовательность ограничена. Если заменить каждую скобку в правой части на 1, то мы увеличим правую часть, и равенство превратится в неравенство:
. Покажем, что эта последовательность ограничена. Если заменить каждую скобку в правой части на 1, то мы увеличим правую часть, и равенство превратится в неравенство:
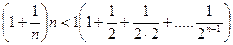


 .
. т.е.
т.е.  . На практике значительно чаще используют сложные проценты. В этом случае размер вклада ежегодно будет увеличиваться в одно и тоже число раз, т.е.
. На практике значительно чаще используют сложные проценты. В этом случае размер вклада ежегодно будет увеличиваться в одно и тоже число раз, т.е. 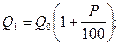
 ;
;  . Если начислять проценты по вкладам не один раз в году, а n раз, то при том же ежегодном приросте P% процент начисления за
. Если начислять проценты по вкладам не один раз в году, а n раз, то при том же ежегодном приросте P% процент начисления за  часть года составит
часть года составит  , а размер вклада за t лет при nt начислениях составит: Qt=Q0
, а размер вклада за t лет при nt начислениях составит: Qt=Q0 
 т.е.
т.е.
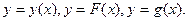 и т.д.
и т.д. и y=
и y=  и т.д.
и т.д. находится из условий
находится из условий  . Поскольку x1=2, x2=3 корни квадратного уравнения стоящего под знаком логарифма то это условие выполняется на двух полубесконечных интервалах (-∞,2) и (3, +∞).
. Поскольку x1=2, x2=3 корни квадратного уравнения стоящего под знаком логарифма то это условие выполняется на двух полубесконечных интервалах (-∞,2) и (3, +∞). область ее определения находится из того, что
область ее определения находится из того, что  или -1≤
или -1≤ 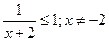
 и
и  , отсюда область определения состоит из двух полубесконечных промежутков(-∞,-3]и[-1, +∞). Функция может иметь прикладной характер и область ее определения будет определяться реальными значениями входящих параметров.
, отсюда область определения состоит из двух полубесконечных промежутков(-∞,-3]и[-1, +∞). Функция может иметь прикладной характер и область ее определения будет определяться реальными значениями входящих параметров.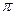 .
. , определенная на множестве Y с областью значений X называется обратной.
, определенная на множестве Y с областью значений X называется обратной.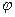 (x) от переменной x, определенной на множестве X с областью значений U. Тогда заданная на множестве X функция y=f [φ(x)] называется сложной функцией.
(x) от переменной x, определенной на множестве X с областью значений U. Тогда заданная на множестве X функция y=f [φ(x)] называется сложной функцией. . Функция называется неявной, если она задана уравнением F(x,y)=0. не разрешенным относительно зависимой переменной.
. Функция называется неявной, если она задана уравнением F(x,y)=0. не разрешенным относительно зависимой переменной.
 ,
,  - существует число
- существует число 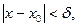 выполняется неравенство
выполняется неравенство 
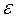 - окрестности точки A можно найти такую
- окрестности точки A можно найти такую  -окрестность, соответствующее значение функции f(x),будет находиться в
-окрестность, соответствующее значение функции f(x),будет находиться в 
 ,или
,или  .
. 
 и
и 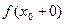 они равны то существует
они равны то существует  и
и  . Если же A1 ≠A2, то
. Если же A1 ≠A2, то  не существует.
не существует.


