
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение поверхности и линии в пространствеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1) Основные понятия Поверхность в пространстве, как правило можно рассматривать как геометрическое место точек удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в т.О1.есть геометрическое место точек удаленных от т. О1 на расстояние R. Прямоугольная система координат Oxyz позволяет однозначно установить соответствие между точками пространства и тройками чисел x,y,z- их координатами. Свойства, общие всем точкам, можно записать в виде уравнения, связывающего координаты всех точек поверхности. Уравнение данной поверхности в прямоугольной системе координат Oxyz называют уравнением вида F(x,y,z)=0, с тремя переменными x,y,z которому удовлетворяют координаты каждой точки лежащей на поверхности и не удовлетворяют координаты точек не лежащие на поверхности. 2) Уравнение линии в пространстве Линию в пространстве можно рассматривать как линию пересечения двух поверхностей или как геометрическое место точек общих двум поверхностям. Если F1(x,y,z)=0 и F2(x,y,z) уравнения двух поверхностей, то координаты линии их пересечения (L) должно удовлетворять системе двух уравнений с тремя неизвестными
Линию в пространстве можно рассматривать и как траекторию движения точки. В этом случае ее задают векторным уравнением r=r(t) или параметрическим уравнениями.
3) Уравнение прямой в пространстве 1. Векторное уравнение прямой Положение прямой в пространстве вполне определено, если задать какую-либо точку M0 на прямой и вектор

      векторы точек M0 и M соответственно через векторы точек M0 и M соответственно через  и и  . Очевидно, что . Очевидно, что  = =  + +  . Вектор . Вектор  М, лежащий на прямой L параллелен направляющему вектору М, лежащий на прямой L параллелен направляющему вектору  , поэтому , поэтому  M=t M=t  , где t- скалярный множитель, называемый параметром, может принимать различные значения в зависимости от положения точки M на прямой (рис.1.). Тогда уравнение можно записать в виде , где t- скалярный множитель, называемый параметром, может принимать различные значения в зависимости от положения точки M на прямой (рис.1.). Тогда уравнение можно записать в виде  = =  +t +t  - векторное уравнение прямой. - векторное уравнение прямой.
2. Параметрическое уравнение прямой Поскольку
исключая из параметрического уравнения прямой t получим:
4. Уравнение прямой проходящей через две точки Пусть прямая L проходит через точки M1(x1,y1,z1) и M2(x2,y2,z2). В качестве направляющего вектора
5. Угол между прямыми Пусть L1 и L2 заданы уравнениями
Если L1 перпендикулярна L2, то в этом случае cosφ=0, следовательно
Если L1 || L2, то векторы
4) Уравнение плоскости в пространстве.
Простейшей поверхностью является плоскость. Плоскость в пространстве Oxyz можно задать различными способами и каждому из них соответствует конкретное уравнение. 1. Уравнение плоскости проходящей через точку перпендикулярно вектору. Пусть в пространстве Oxyz плоскость Q задана точкой M0(x0,y0,z0) и вектором
-это уравнение плоскости проходящей через данную точку перпендикулярную вектору 2. Общее уравнение плоскости Рассмотрим общее уравнение первой степени с тремя переменными x,y и z.
Полагая, что по крайней мере, один из коэффициентов A,B или C≠0, например B≠0, перепишем его в виде:
Сравнивая полученное уравнение с ранее полученным (1) видим, что последнее является уравнением плоскости с нормальным вектором Частные случаи: а) Если D=0, то б) Если C=0, имеем в) Если C=D=0, то плоскость проходит через т.O(0,0,0) и || Oz, то есть проходит через ось Oz; г) Если A=B=0, то Cz+D=0, то есть Z= д) Если A=B=D=0, то Cz=0, то есть Z=0, это уравнение плоскости Oxy. 3. Уравнение плоскости, проходящей через три точки. Три точки в пространстве не лежащие на одной прямой определяют единственную плоскость. Найдем уравнение плоскости Q,проходящей через три данных точки M1(x1,y1,z1), M2(x2,y2,z2) и M3(x3,y3,z3), не лежащие на одной прямой. Возьмем на плоскости произвольную точку M(x,y,z) и составим векторы
-это уравнение есть уравнение плоскости, проходящей через три точки. 4. Уравнение плоскости в отрезках Пусть плоскость отсекает на осях Ox, Oy и Oz соответственно отрезки
5. Нормальное уравнение плоскости Положение плоскости Q можно определить заданием единичного вектора
            Пусть OK=P, а α, β и γ-углы, образованные вектором Пусть OK=P, а α, β и γ-углы, образованные вектором  с осями Ox, Oy и Oz. Тогда с осями Ox, Oy и Oz. Тогда  = =  . Возьмем на плоскости произвольную точку M(x,y,z) и соединим ее с началом координат. Образуем вектор . Возьмем на плоскости произвольную точку M(x,y,z) и соединим ее с началом координат. Образуем вектор
точки M на плоскости Q проекция вектора
6. Угол между двумя плоскостями пусть заданы две плоскости Q1 и Q2:
Под углом между плоскостями понимают один из двугранных углов образованных этими плоскостями. Угол φ между нормальными векторами полученное равенство есть условие перпендикулярности Q1 и Q2. Если Q1 || Q2, то 7. Расстояние от точки до плоскости.
 . Найдем d- расстояние от точки до плоскости. Расстояние d от точки M0 до плоскости Q равно модулю проекции вектора M1M0 (Рис.3), где M1(x1,y1,z1)- произвольная точка плоскости Q на направление нормального вектора . Найдем d- расстояние от точки до плоскости. Расстояние d от точки M0 до плоскости Q равно модулю проекции вектора M1M0 (Рис.3), где M1(x1,y1,z1)- произвольная точка плоскости Q на направление нормального вектора  =(A,B,C). Следовательно =(A,B,C). Следовательно   = =
     = = 
    
Так как т.M1 принадлежит Q, то
    ,и ,и  , тогда уравнение примет вид: , тогда уравнение примет вид:
 . .
8 .Угол между прямой и плоскостью Пусть плоскость задана уравнением
 
  
    Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость. Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость.
Пусть φ- угол между Q и L, а
Если L || Q, то Если L 9. Пересечение прямой с плоскостью Найти точку пересечения прямой
Для этого надо решить систему этих уравнений. Проще всего это сделать если записать уравнение прямой в параметрической форме:
Подставляя эти значения в уравнение плоскости получим Поверхности второго порядка 1) Цилиндрические поверхности. Поверхность, образованная движением прямой L, которая перемещается в пространстве, сохраняя постоянное направление, и пересекает каждый раз некоторую кривую K, называется цилиндрической поверхностью или цилиндром. При этом кривая K- называется направляющей, а L – образующей цилиндра. Будем рассматривать цилиндрические поверхности, направляющие которых лежат в одной из координатных плоскостей, а бразующие || координатной оси, то есть перпендикулярно этой плоскости. Пусть в Oxy лежит линия K, а ее уравнение F(x,y)=0. Построим цилиндр с образующими || оси Oz и направляющей K.
         Возьмем на цилиндре любую точку M(x,y,z). Она лежит на какой-то образующей. Пусть т.N- точка пересечения этой образующей с плоскостью Oxy. Следовательно, точка N лежит на кривой K, и ее координаты удовлетворяют уравнению линии K. Но точка M имеет такие же абсциссу x и ординату y, что и точка N. Возьмем на цилиндре любую точку M(x,y,z). Она лежит на какой-то образующей. Пусть т.N- точка пересечения этой образующей с плоскостью Oxy. Следовательно, точка N лежит на кривой K, и ее координаты удовлетворяют уравнению линии K. Но точка M имеет такие же абсциссу x и ординату y, что и точка N.
Следовательно, этому уравнению удовлетворяют и координаты точки M(x,y,z), так как оно не содержит Z. Так как M- любая точка цилиндра то уравнение F(x,y)=0, и будут уравнения цилиндра с образующими || оси Oz. В случае если образующая || оси Oy F(x,y)=0, если образующая || оси Ox; F(y,z)=0. Название цилиндра определяется формой направляющей. Если направляющей служит эллипс, в плоскости Oxy, то цилиндрическая поверхность называется эллиптическим цилиндром частный случай эллипса- окружность дает круговой цилиндр и т.д. все эти поверхности называются цилиндрами второго порядка, т.к. их уравнения есть уравнения второй степени. 2) Поверхности вращения. Конические поверхности. Поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в ее плоскости называется поверхностью вращения. Пусть некоторая кривая L лежит в плоскости Oyz. Уравнения этой кривой запишут в виде:
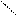   
       Найдем уравнение поверхности образованное вращением кривой L вокруг оси Oz. Для этого возьмем на поверхности произвольную т.M(x,y,z). Проведем через M плоскость перпендикулярную оси Oz. Обозначим точки пересечения ее с осью Oz и кривой L соответственно O1 и N. Тогда O1(0,0,z), а N(0, Найдем уравнение поверхности образованное вращением кривой L вокруг оси Oz. Для этого возьмем на поверхности произвольную т.M(x,y,z). Проведем через M плоскость перпендикулярную оси Oz. Обозначим точки пересечения ее с осью Oz и кривой L соответственно O1 и N. Тогда O1(0,0,z), а N(0,  ,z1). Отрезки O1M и O1N являются радиусами одной и той же окружности. Поэтому O1M=O1N, но ,z1). Отрезки O1M и O1N являются радиусами одной и той же окружности. Поэтому O1M=O1N, но
Так как точка N лежит на кривой L, то ее координаты удовлетворяют уравнениям (1). Стало быть, F(y1,z1)=0,исключая вспомогательные координаты y1 и z1 придем к соотношению
Это уравнение - поверхности вращения, ему удовлетворяют координаты любой точки M этой поверхности и не удовлетворяют координаты точек не лежащих на поверхности вращения. Если кривая вращается вокруг других осей Ox и Oy, то уравнение будет носить аналогичный характер соответственно Поверхность, образованная прямыми линиями, проходящими через данную точку p и пересекающими данную плоскую линию L(не проходящую через p) называются конической поверхностью или конусом. При этом L- направляющая конуса p- ее вершина, а прямая описывающая поверхность называется образующей. Пусть направляющая L задана уравнениями:

 

       Возьмем на поверхности конуса произвольную точку M(z,y,z)(рис.3). Образующая, проходящая через точки P и M, пересекает направляющую L в некоторой точке N(x1,y1,z1) координаты точки N удовлетворяют выше записанным соотношениям, следовательно: Возьмем на поверхности конуса произвольную точку M(z,y,z)(рис.3). Образующая, проходящая через точки P и M, пересекает направляющую L в некоторой точке N(x1,y1,z1) координаты точки N удовлетворяют выше записанным соотношениям, следовательно: 
А канонические уравнения образующих проходящих через т.P и т. N имеют вид.
Исключая из этих уравнений Пример: составить уравнение конуса с вершиной в т.О(0,0,0).Если направляющая - эллипс
Решение: Каноническое уравнение образующих, проходящих через т.О(0,0,0) и т.N(x1,y1,z1), полученную при пересечении образующей OM с эллипсом, будет 3) Канонические уравнения поверхностей второго порядка. По заданному уравнению поверхности второго порядка(те поверхности, уравнение которой в прямоугольной системе координат является алгебраическим уравнением второго порядка) будем определять ее геометрическим вид. Для этого применим так называемый метод сечений: исследование вида поверхности будем производить при помощи изучения линий пересечения данной поверхности с координатными плоскостями или плоскостями им параллельными. а) Эллипсоид Исследуем поверхность, заданную уравнением:
Рассмотрим сечения поверхности описываемой этим уравнением с плоскостями || плоскости Oxy. Уравнения этих плоскостей Z=h, где h- любое число. Линия, получаемая в сечении, будет определяться двумя уравнениями:
Исследуем это уравнение. а) Если |h|>c, c>0, то б) Если |h|<c, то уравнения (1) можно записать в виде: т.е. линия пересечения есть эллипс с полуосями:
При этом, чем меньше |h|, тем больше полуоси
 
 ,b,c- называются полуосями ,b,c- называются полуосями
эллипсоида, если б ) Однополостный гиперболоид. Исследуем поверхность, заданную уравнением:
Пересекая эту поверхность плоскостью Z=h, получим линию пересечения, уравнение которой имеет вид:
Как видно, этой линий является эллипс с полуосями:
  Полуоси Полуоси  1 и b1 достигают min при h=0, 1 и b1 достигают min при h=0,  1= 1=  и b1=b. При возрастании |h| и b1=b. При возрастании |h|  1 и b1 будут возрастать. 1 и b1 будут возрастать.

    Если пересекать эту поверхность плоскостями x=h и y=h, то в сечении получим гиперболы. Найдем, например, линию пересечения нашей поверхности с полуосью Oyz, уравнение которой x=0. Подставляя, получим: Если пересекать эту поверхность плоскостями x=h и y=h, то в сечении получим гиперболы. Найдем, например, линию пересечения нашей поверхности с полуосью Oyz, уравнение которой x=0. Подставляя, получим:
  -это гипербола -это гипербола
Анализ сечений показывает, что поверхность, определяемая нашим уравнением, имеют форму бесконечно расширяемой трубки. Эта поверхность называется однополостным гиперболоидом (рис.5.). с ) Двухполосной гиперболоид Пусть поверхность задана уравнением:
Если эту поверхность пересечь плоскостью Z=h, получим линию пересечения, описываемую уравнениями: Отсюда следует, что: а) если |h|<c, то Z=h не пересекает поверхность; б) если |h|=с, то плоскости Z=c касаются данной поверхности в точках (0,0,c) и (0,0,-c); в) если |h|>c, то уравнения можно записать так:
 Пересекая поверхность координатными плоскостями Oyz(x=0) и Oxz(y=0), получим в сечении гиперболы, уравнения которых соответственно: Пересекая поверхность координатными плоскостями Oyz(x=0) и Oxz(y=0), получим в сечении гиперболы, уравнения которых соответственно: 
  
    | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |


 -это уравнение линии в пространстве.
-это уравнение линии в пространстве. -проекции вектора r на оси координат.
-проекции вектора r на оси координат.
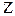
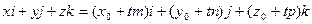 . Отсюда
. Отсюда  - параметрическое уравнение прямой в пространстве.
- параметрическое уравнение прямой в пространстве.
 - каноническое уравнение прямой.
- каноническое уравнение прямой. , т.е.
, т.е.  , следовательно, m=x2-x1, n=y2-y1, p=z2-z1. поскольку наша прямая проходит через т.M1(x,y,z) то каноническое уравнение примет вид:
, следовательно, m=x2-x1, n=y2-y1, p=z2-z1. поскольку наша прямая проходит через т.M1(x,y,z) то каноническое уравнение примет вид:
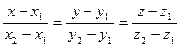 - уравнение прямой проходящей через две точки.
- уравнение прямой проходящей через две точки.
 . Под углом между этими прямыми понимают угол между направляющими векторами
. Под углом между этими прямыми понимают угол между направляющими векторами  или
или

 .
. =(A,B,C) перпендикулярным этой плоскости. Возьмем на плоскости произвольную точку M(x,y,z) и составим вектор
=(A,B,C) перпендикулярным этой плоскости. Возьмем на плоскости произвольную точку M(x,y,z) и составим вектор  . Так как
. Так как  перпендикулярен Q, то вектор
перпендикулярен Q, то вектор  , т.е.
, т.е.
 (1)
(1)
 . Итак уравнение (2) определяет в пространстве Oxyz некоторую плоскость. Это уравнение и называется общим уравнением плоскости.
. Итак уравнение (2) определяет в пространстве Oxyz некоторую плоскость. Это уравнение и называется общим уравнением плоскости. . Этому уравнению отвечает т.O(0,0,0)-начало координат. Следовательно, эта плоскость проходит через начало координат;
. Этому уравнению отвечает т.O(0,0,0)-начало координат. Следовательно, эта плоскость проходит через начало координат; , вектор
, вектор  , плоскость || плоскости Oxy;
, плоскость || плоскости Oxy;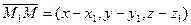 ;
;  и
и  . Эти векторы компланарны. Используя условия компланарности трех векторов (их смешанное произведение=0) получим:
. Эти векторы компланарны. Используя условия компланарности трех векторов (их смешанное произведение=0) получим:
 т.е.
т.е. (1)
(1)
 =0. Раскрыв определитель имеем:
=0. Раскрыв определитель имеем: или
или  -уравнение плоскости в отрезках на осях.
-уравнение плоскости в отрезках на осях.


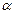
 =
=  =(x,y,z). При любом положении
=(x,y,z). При любом положении
 т.е.
т.е.  или
или  - это нормальное уравнение плоскости. Зная координаты r и e можно его переписать в следующей форме:
- это нормальное уравнение плоскости. Зная координаты r и e можно его переписать в следующей форме:

 (A1,B1,C1) и
(A1,B1,C1) и  (A2,B2,C2) плоскостей Q1 Q2 равен одному из этих углов. Поэтому
(A2,B2,C2) плоскостей Q1 Q2 равен одному из этих углов. Поэтому  или
или  . Для нахождения острого угла следует взять модуль правой части. Если Q1 перпендикулярен Q2, то вектор
. Для нахождения острого угла следует взять модуль правой части. Если Q1 перпендикулярен Q2, то вектор  =0, то есть
=0, то есть  .
. - это условие параллельности Q1 и Q2.
- это условие параллельности Q1 и Q2. , а прямая L уравнением
, а прямая L уравнением

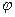
 Рис.4
Рис.4 - угол между
- угол между  ,а
,а  и так как Sinφ≥0 получим:
и так как Sinφ≥0 получим: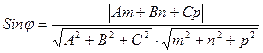 -искомый результат.
-искомый результат. , поэтому
, поэтому  =0, то есть
=0, то есть  является условием параллельности L и Q.
является условием параллельности L и Q. Q, то
Q, то  -условия перпендикулярности L и Q.
-условия перпендикулярности L и Q. с плоскостью
с плоскостью 
 или
или  , если L не || Q, то есть если
, если L не || Q, то есть если 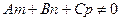 , то получим
, то получим  , подставляя t в записанные выше уравнение прямой в параметрической форме координат, получим их значения в точке пересечения L и Q.
, подставляя t в записанные выше уравнение прямой в параметрической форме координат, получим их значения в точке пересечения L и Q. (1)
(1)
 N (0,y1,z1)
N (0,y1,z1)
 M (x,y,z)
M (x,y,z)
 а
а  тогда
тогда 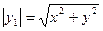 или
или  , кроме того Z1=Z.
, кроме того Z1=Z. - это искомое уравнение.
- это искомое уравнение.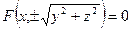 и
и  . Так, например, вращая прямую y=z вокруг оси Oz получим поверхность вращения описываемую уравнением
. Так, например, вращая прямую y=z вокруг оси Oz получим поверхность вращения описываемую уравнением  или
или  - это конус второго порядка
- это конус второго порядка
 ,
,  получим уравнение конической поверхности связывающее текущие координаты x, y и z.
получим уравнение конической поверхности связывающее текущие координаты x, y и z. , лежащий в плоскости Z1=с.
, лежащий в плоскости Z1=с. учитывая, что Z1=с, получим:
учитывая, что Z1=с, получим:  , откуда
, откуда  ; Подставляя значения x1 и y1 в уравнение эллипса, с учетом того, что N(x1,y1,z1) лежит на эллипсе, можно получить
; Подставляя значения x1 и y1 в уравнение эллипса, с учетом того, что N(x1,y1,z1) лежит на эллипсе, можно получить  , подставляя сюда ранее полученное значения x1 и y1 получим
, подставляя сюда ранее полученное значения x1 и y1 получим  или окончательно
или окончательно  - это и есть уравнение конуса.
- это и есть уравнение конуса.
 (1)
(1) . Точек пересечения нашей поверхности с плоскостями Z=h не существует;
. Точек пересечения нашей поверхности с плоскостями Z=h не существует; =1
=1 ;
; 
 .
.  =1
=1 или
или 


 и
и 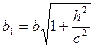




 - эти уравнения определяют эллипс, полуоси которого возрастают с ростом |h|.
- эти уравнения определяют эллипс, полуоси которого возрастают с ростом |h|.




