
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 5. Пространственные фигурыСодержание книги Поиск на нашем сайте Аналитический способ Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно кусочное задание, то есть различное для различных значений аргумента. Табличный способ Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции: Графический способ Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции. Рекурсивный способ Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения. Словесный способ Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные. ВОПРОС 2. СВОЙСТВА ФУНКЦИЙ 1) Область определения функции и область значений функции. Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена. В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции. Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
3) Промежутки знакопостоянства функции. Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
4) Монотонность функции. Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции. Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции. Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат. Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.
6) Ограниченная и неограниченная функции. Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x. Если такого числа не существует, то функция - неограниченная.
7) Периодическость функции. Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. ВОПРОС 3. ОБРАТНАЯ ФУНКЦИЯ Пусть функция Другими словами, об обратной функции Функции f и g называют взаимно обратными. Зачем вообще рассматривать понятие обратных функций? Это вызвано задачей решения уравнений Примеры нахождения взаимнообратных функций. Например, требуется решить уравнение Решениями являются точки Функции косинус и арккосинус как раз являются обратными на области определения. ВОПРОС 4. ОСНОВНЫЕ ПОНЯТИЯ СТЕРЕОМЕТРИИ А1. Через любые три точки не лежащие на одной прямой проходит плоскость и проитом тока одна. Следствия: Основные понятия стереометрии (точка, прямая, плоскость, пространство).
БИЛЕТ. ЧИСЛОВАЯ ОКРУЖНОСТЬ Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам. Единичной окружностью называют окружность радиуса 1. Определение.
Теперь мы в состоянии сделать общий вывод о решении уравнения t = a:
Билет 22 арктангенс и арккотангенс. Решение уравнений tg x=a, ctg x=a 23 билет Однородные тригонометрические уравнения Уравнения вида a sin x+ b cos x= 0 называют однородными тригоном. уравнениями первой степени Алгоритм решения уравнений Tg х tg 2x = ————— Tg2 х Другие формулы двойного аргумента:
31.Преобразование сумм тригонометрических функций в произведение Теорема. Для любых Доказательство. Все четыре формулы доказываются преобразованием правой части в сумму
32 .Преобразование произведения тригонометрических функций в суммы
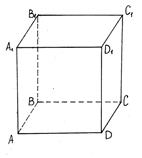
33. Параллелепипед Параллелепипед - призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них — параллелограмм.
Типы параллелепипеда Различается несколько типов параллелепипедов: · Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники; · Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — параллелограммы; · Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям. Основные элементы Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями. Свойства · Параллелепипед симметричен относительно середины его диагонали. · Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам. · Противолежащие грани параллелепипеда параллельны и равны. · Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений Основные формулы Прямой параллелепипед · Площадь боковой поверхности Sб=Ро*h, где Ро — периметр основания, h — высота · Площадь полной поверхности Sп=Sб+2Sо, где Sо — площадь основания · Объём V=Sо*h Куб · Площадь боковой поверхности S=6*h2, где h – высота ребра куба
34. Тетраэдр — правильный многогранник, имеет 4 грани, которые являются правильными треугольниками. Вершин у тетраэдра 4, к каждой вершине сходится 3 ребра, а всего ребер 6. Также тетраэдр является пирамидой.
Треугольники, из которых состоит тетраэдр, называются гранями (АОС, ОСВ, ACB, AOB), их стороны --- ребрами (AO, OC, OB), а вершины --- вершинами (A, B, C, O) тетраэдра. Два ребра тетраэдра, не имеющие общих вершин, называются противоположными... Иногда выделяют одну одну из граней тетраэдра и называют ее основанием, а три другие --- боковыми гранями. Тетраэдр называется правильным, если все его грани — равносторонние треугольники. При этом правильный тетраэдр и правильная треугольная пирамида – это не одно и то же. У правильного тетраэдра все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны. 35. Правильная призма Призмой называется многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а все ребра вне этих граней параллельны между собой. Грани, отличные от оснований, называются боковыми гранями, а их ребра называются боковыми ребрами. Все боковые ребра равны между собой как параллельные отрезки, ограниченные двумя параллельными плоскостями. Все боковые грани призмы являются параллелограммами. Соответствующие стороны оснований призмы равны и параллельны. Прямой называется призма, у которой боковое ребро перпендикулярно плоскости основания, другие призмы называются наклонными. В основании правильной призмы лежит правильный многоугольник. У такой призмы все грани – равные прямоугольники. Поверхность призмы состоит из двух оснований и боковой поверхности. Высотой призмы называется отрезок, являющийся общим перпендикуляром плоскостей, в которых лежат основания призмы. Высота призмы есть расстояние H между плоскостями оснований. Площадью боковой поверхности S б призмы называется сумма площадей ее боковых граней. Площадью полной поверхности S п призмы называется сумма площадей всех ее граней. S п = S б + 2 S,где S – площадь основания призмы, S б – площадь боковой поверхности.
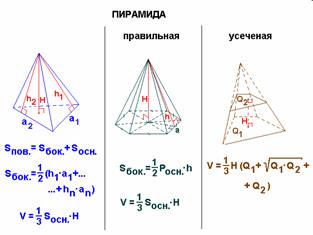
36. Многогранник, у которого одна грань, называемая основанием, – многоугольник, Грани, отличные от основания, называются боковыми. Пирамида называется правильной, если ее основание – правильный многоугольник, а высота проходит через центр основания. Апофемой боковой грани правильной пирамиды называется высота этой грани, проведенная из вершины пирамиды. Плоскость, параллельная основанию пирамиды, отсекает ее на подобную пирамиду и усеченную пирамиду.
Свойства правильных пирамид
Если все боковые ребра равны, то ·высота проектируется в центр описанной окружности; ·боковые ребра образуют с плоскостью основания равные углы. Если боковые грани наклонены к плоскости основания под одним углом, то ·высота проектируется в центр вписанной окружности; ·высоты боковых граней равны; ·площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани
37. Функцию y=f(x), где x принадлежит множеству натуральных чисел, называют функцией натурального аргумента или числовой последовательностью. Обозначают ее y=f(n), или (yn) Последовательности можно задавать различными способами, словесно, так задается последовательность простых чисел: 2, 3, 5, 7, 11 и т.д Считают, что последовательность задана аналитически, если указана формула ее n-го члена: 1) yn = n2 1, 4, 9, 16, …, n2, …
2) yn = C. Такую последовательность называют постоянной или стационарной. Например: 2, 2, 2, 2, …, 2, … 3) yn=2n. Например, 2, 22, 23, 24, …, 2n, … Последовательность называют ограниченной сверху, если все ее члены не больше некоторого числа. Иными словами, последовательность можно назвать ограниченной, если есть такое число М, что выполняется неравенство yn меньше или равно M. Число М называют верхней границей последовательности. Например последовательность: -1, -4, -9, -16, …, - n2; ограничена сверху. Аналогично, последовательность можно назвать ограниченной снизу, если все ее члены больше некоторого числа. Если последовательность ограничена и сверху и снизу она называется ограниченной. Последовательность называют возрастающей, если каждый ее последующий член больше предыдущего. Последовательность называют убывающей, если каждый ее последующий член меньше предыдущего. Возрастающие и убывающие последовательности определяют одним термином – монотонные последовательности. Рассмотрим две последовательности: 1) yn: 1, 3, 5, 7, 9, …, 2n-1, … 2) xn: 1, ½, 1/3, 1/ 4, …, 1/n, … Если мы изобразим члены этой последовательности на числовой прямой, то заметим что, во втором случае члены последовательности сгущаются вокруг одной точки, а в первом случае такого нет. В подобных случаях говорят, что последовательность yn расходится, а последовательность xn сходится. Число b называют пределом последовательности yn, если в любой заранее выбранной окрестности точки b, содержатся все члены последовательности, начиная с некоторого номера. В данном случае мы можем написать:
Если частное прогрессии по модулю меньше единицы, то предел этой последовательности, при х, стремящимся к бесконечности равен нулю. Если последовательность сходится, то только к одному пределу Если последовательность сходится, то она ограничена. Теорема Вейерштрасса: Если последовательность монотонно сходится, то она ограничена. Предел стационарной последовательности равен любому члену последовательности. Свойства: 1) Предел суммы равен сумме пределов 2) Предел произведения равен произведению пределов 3) Предел частного равен частному пределов 4) Постоянный множитель можно вынести за знак предела
Вопрос 38 Геометрическая прогрессия — последовательность чисел b1, b2, b3,.. (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число q (знаменатель прогрессии), где b1≠0, q≠0. Сумма бесконечной геометрической прогрессии – это предельное число, к которому сходится последовательность прогрессии. Говоря иначе, какой бы длинной не была геометрическая прогрессия, сумма ее членов не больше какого-то определенного числа и практически равна этому числу. Оно и называется суммой геометрической прогрессии. Не любая геометрическая прогрессия имеет такую предельную сумму. Она может быть только у такой прогрессии, знаменатель которой – дробное число меньше 1. Сумма бесконечной геометрической прогрессии вычисляется по формуле:
Вопрос39
· Вычисление производных · · · · · · · · (sin x)' = cos x; · (cos x)' = - sin x; · · · · Вопрос40 Построение графиков ф-ций 1. Найти область определения функции, 2. Исследовать функцию на четность. 3. Исследовать функцию на периодичность. 4. Найти точки пересечения графика с осями координат. 5. Определить промежутки знакопостоянства. 6. Исследовать функцию на границах области. Найти асимптоты. 7. Исследовать функцию на экстремум. 8. Составить таблицу значений функции для некоторых значений аргумента. 9. Используя все полученные результаты,построить график функции.
Вопрос41 Теорема. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна к наклонной.
Доказательство:
Пусть
Скрещивающиеся прямые.
Невозможно. Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общим перпендикуляром двух скрещивающихся прямых называется отрезок, концы которого лежат на этих прямых, и он перпендикулярен каждой из этих прямых. Две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром параллельных плоскостей, каждая из которых проходит через одну прямую параллельно другой.
Имеем две скрещивающиеся прямые a и b. Через каждую из них проведена плоскость(плоскость Аналитический способ Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно кусочное задание, то есть различное для различных значений аргумента. Табличный способ Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции: Графический способ Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции. Рекурсивный способ Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения. Словесный способ Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные. ВОПРОС 2. СВОЙСТВА ФУНКЦИЙ 1) Область определения функции и область значений функции. Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена. В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции. Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
3) Промежутки знакопостоянства функции. Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
4) Монотонность функции. Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции. Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции. Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат. Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.
6) Ограниченная и неограниченная функции. Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x. Если такого числа не существует, то функция - неограниченная.
7) Периодическость функции. Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. ВОПРОС 3. ОБРАТНАЯ ФУНКЦИЯ Пусть функция Другими словами, об обратной функции Функции f и g называют взаимно обратными. Зачем вообще рассматривать понятие обратных функций? Это вызвано задачей решения уравнений Примеры нахождения взаимнообратных функций. Например, требуется решить уравнение Решениями являются точки Функции косинус и арккосинус как раз являются обратными на области определения. ВОПРОС 4. ОСНОВНЫЕ ПОНЯТИЯ СТЕРЕОМЕТРИИ А1. Через любые три точки не лежащие на одной прямой проходит плоскость и проитом тока одна. Следствия: Основные понятия стереометрии (точка, прямая, плоскость, пространство).
ВОПРОС 5. ПРОСТРАНСТВЕННЫЕ ФИГУРЫ 5. Пространственные фигуры Среди пространственных фигур выделяют многогранники – тела, поверхности которых состоят из конечного числа многоугольников, называемых гранями многогранника. Стороны этих многоугольников называют ребрами, вершины – вершинами многогранника. Диагонали многогранника- отрезки, соединяющие вершины, не принадлежащие одной грани. Примеры многогранников: (пространственные фигуры) КУБ- многогранник, поверхность которого состоит из 6ти квадратов. ПАРАЛЛЕЛЕПИПЕД- многогранник, поверхность которого состоит из 6ти параллелограммов. Параллелепипед, у которого все грани- прямоугольники, называется прямоугольным. ПРИЗМА- многогранник, поверхность которого состоит из двух равных многоугольников, называемых основаниями призмы, и параллелограммов, имеющих общие стороны с каждым из оснований (боковые грани призмы). Ребра, не лежащие в основаниях призмы, называются боковыми ребрами. Призма, боковыми гранями которой являются прямоугольники, называется прямой. В противном случае призма называется наклонной. Призмы бывают треугольные, четырехугольные, пятиугольные и т.д. в зависимости от того, какие многоугольники лежат в их основаниях: треугольники, четырехугольники, пятиугольники и т.д.. ПИРАМИДА- многогранник, поверхность которого состоит из многоугольника, называемого основанием пирамиды, и треугольников, имеющих общую вершину – боковые грани пирамиды. Общая их вершина называется вершиной пирамиды. Ребра, сходящиеся в вершине пирамиды, называются боковыми ребрами. Пирамида, в основании которой лежит правильный многоугольник и все боковые ребра которой равны, называется правильной. Пирамиды бывают треугольные, четырехугольные, пятиугольные и т.д. в зависимости от того, какие многоугольники лежат в их основаниях: треугольники, четырехугольники, пятиугольники и т.д.. Треугольная пирамида называется также тетраэдром. Пространственные фигуры, не являющиеся многогранниками: СФЕРА- фигура, состоящая из всех точек пространства, удаленных от данной точки, называемой центром, на данное расстояние, называемое радиусом. ШАР- фигура, состоящая из всех точек пространства, удаленных от данной точки, называемой центром, на расстояние, не превосходящее данное, называемое радиусом. Сфера с тем же центром и того же радиуса, что и данный шар, называется поверхностью шара. Также примерами пространственных фигур является цилиндр и конус. P.S.Я лично буду учить ТОЛЬКО про сами фигуры, но на стр. 312(пар. 35) написано еще что такое подобие, движение в пространстве. Захотите-посмотрите. 6. Параллельность прямых в пространстве ОПРЕДЕЛЕНИЕ: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. ТЕОРЕМА: Через точку в пространстве, не принадлежащую данной прямой, проходит единственная прямая, параллельная данной прямой. Док-во- Пусть точка А не принадлежит прямой b. Проведем через эту прямую и точку А плоскость альфа. Эта плоскость единственна. В плоскости через точку А проходит единственная прямая, назовем ее а, параллельная прямой b. Она и будет искомой прямой, параллельной данной. Прямые в пространстве могут не пересекаться, но и не быть параллельными. ОПРЕДЕЛЕНИЕ: Две прямые в пространстве называются скрещивающимися, если через них нельзя провести плоскость. Также два отрезка скрещиваются, если они лежат на скрещивающихся прямых. Две прямые Лежат в одной плоскости Не лежат в одной плоскости 1)имеют общую точку(пересекаются) Не лежат в одной плоскости (скрещиваются) 2)не имеют общих точек(параллельны) ПРИМЕР 1: Через каждые две параллельные прямые можно провести плоскость. Таким образом, если имеются три параллельные прямые, не лежащие в одной плоскости, то через них можно провести три плоскости, если 4 прямые, то 6 плоскостей, если n прямых, то через каждую можно провести n-1 плоскость. Учитывая, что при общем подсчете каждая плоскость будет считаться дважды, получаем общее число плоскостей: n(n-1)/2. ПРИМЕР 2(признак скрещивающихся прямых): Если одна прямая лежит в одной плоскости, а другая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти две прямые скрещивающиеся. Пусть прямая а лежит в плоскости альфа, а прямая b пересекает плоскость альфа в точке В, не принадлежащей прямой а. Если бы прямые а и b лежали в одной плоскости, то в этой плоскости лежали бы прямая а и точка В. Поскольку через прямую и точку вне этой прямой проходит единственная
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.05 с.) |

 строго монотонная (возрастающая или убывающая) и непрерывная на области определения
строго монотонная (возрастающая или убывающая) и непрерывная на области определения  , область значений этой функции
, область значений этой функции 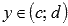 , тогда на интервале
, тогда на интервале 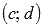 определена непрерывная строго монотонная функция
определена непрерывная строго монотонная функция  с областью значений
с областью значений  , которая является обратной для
, которая является обратной для  .
. .
.


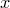 и
и  справедливы равенства
справедливы равенства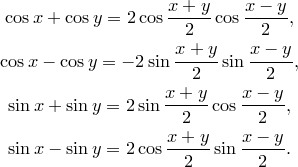

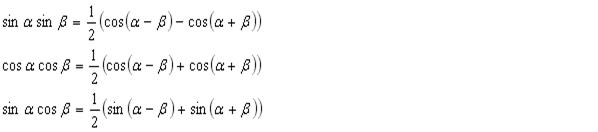




 называется предел отношения приращения функции к приращению переменной, то есть
называется предел отношения приращения функции к приращению переменной, то есть 


 [2]
[2] [3]
[3]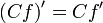
 …(g ≠ 0)
…(g ≠ 0)
 ;
;
 ;
;
 ;
;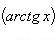
 ;
;
 ;
;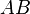 — перпендикуляр к плоскости
— перпендикуляр к плоскости 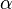 ,
, 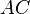 — наклонная и
— наклонная и  — прямая в плоскости
— прямая в плоскости 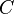 и перпендикулярная проекции
и перпендикулярная проекции 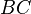 . Проведем прямую
. Проведем прямую  параллельно прямой
параллельно прямой 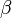 (параллельные прямые определяют плоскость, причем только одну). Прямая
(параллельные прямые определяют плоскость, причем только одну). Прямая 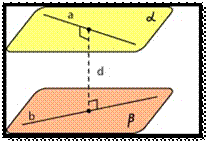 Скрещивающиеся прямые не параллельны и не пересекаются. Они лежат в параллельных плоскостях, и поместить их в одну плоскость
Скрещивающиеся прямые не параллельны и не пересекаются. Они лежат в параллельных плоскостях, и поместить их в одну плоскость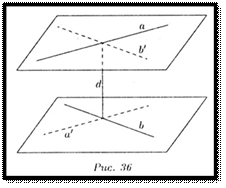 Пример:
Пример: проходит через а, плоскость проходит через b), параллельная другой прямой. Отрезки параллельных прямых, заключенные между параллельных прямых, равны.
проходит через а, плоскость проходит через b), параллельная другой прямой. Отрезки параллельных прямых, заключенные между параллельных прямых, равны.


