
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ищем прямые пересечения плоскости сечения с гранями многогранника, для этогоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
· ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости); · параллельные грани плоскость сечения пересекает по параллельным прямым. Пример: Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Построим сечение, проходящее через точки M, N, L
. Соединим точки M и L, лежащие в плоскости AA1D1D
Пересечем прямую ML (принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.
Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости. X1 N пересекается с ребром A1B1 в точке К.
Соединим точки K и M, лежащие в одной плоскости AA1B1B.
Найдем прямую пересечения плоскости сечения с плоскостью DD1C1C: пересечем прямую ML (принадлежащую сечению) с ребром DD1, они лежат в одной плоскости AA1D1D, получим точку X2; пересечем прямую KN (принадлежащую сечению) с ребром D1C1, они лежат в одной плоскости A1B1C1D1, получим точку X3;
Точки X2 и X3 лежат в плоскости DD1C1C. Проведем прямую X2 X3, которая пересечет ребро C1C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.
MKNTPL - искомое сечение .
16. Функция y=sinx, ее свойства и график. Функция y=cosx, ее свойства и график.
Синусоида:
Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная. Функция нечетная: sin(−x)=−sin x для всех х ∈ R. Функция периодическая с наименьшим положительным периодом 2 π: sin(x+2 π· k) = sin x, где k ∈ Z для всех х ∈ R. sin x = 0 при x = π·k, k ∈ Z. sin x > 0 (положительная) для всех x ∈ (2π·k, π+2π·k), k ∈ Z. sin x < 0 (отрицательная) для всех x ∈ (π+2π·k, 2π+2π·k), k ∈ Z.
Косинусоида:
Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная. Функция четная: cos(−x)=cos x для всех х ∈ R.
Функция периодическая с наименьшим положительным периодом 2 π: cos(x+2 π· k) = cos x, где k ∈ Z для всех х ∈ R.
17. Периодичность функций y=sinx, y=cosx.
Функцию y=f(x), x принадлежит X, называют периодической, если существует такое отличное от нуля число T, что для любого x из множества X выполняется двойное равенство: f(x-T)=f(x)=f(x+T). Число T, удовлетворяющее указанному условию, называют периодом функции y=f(x).
Отсюда следует, что, поскольку для любого x справедливы равенства Sin(x-2п)=sinx=sin(x+2п) и Cos(x-2п)=cosx=cos(x+2п) Функции y=sinx, y=cosx являются периодическими, причем число 2п служит периодом и той и другой функции.
Любое число вида 2пk, где k=+ - 1, + - 2, + - 3…, является периодом функций y=sinx, y=cosx; 2п – основной период и той и другой функции.
Пример: y=sin3x Пусть T – основной период функции y=sinx. Введем обозначение f(x)=sin3x. Тогда F(x+T)=sin3(x+T)=sin(3x+3T). Чтобы число T было периодом функции, должно выполняться тождество sin(3x+3T)=sin3x. Значит, 3T=2пn. Но поскольку речь идет о нахождении основного периода, получаем T=2п\3.
Преобразование графиков тригонометрических функций 1) Зная график y = f(x) посторить график y = m*f(x), где m – положительное число a. Если m>1: ординаты точек исходного графика функции (y=f(x)) умножаются на число m и получаются уже ординаты искомого графика (y=m*f(x). Такое преобразование обычно называют растяжением от оси х с коэффициентом “m”. b. Если m<1: это уже не растяжение, а сжатие к оси x c коэффициентом 2) Зная график функции y = f(x) построить график функции y = m*f(x), где m = -1 a. По сути дела, из графика y = f(x) нужно получить график y = -f(x), что делается симметрическим преобразованием исходного графика, тобишь, если была точка (0;1), то она переходит в точку (0;-1) и т.д.
3) Зная график функции y = f(x),построить график функции y = m*f(x), где m – отрицательное число a. Все довольно просто i. Строим график y = f(x) ii. Растягиваем или сужаем его относительно оси x (в зависимости от положительного коэффициента |m|) iii. Растянутый/сжатый график отображаем симметрично оси x 4) Зная график функции y = f(x), построить график функции y = f(k*x), где k –положительное число a. Вообще график функции y = f(k*x) получается из графика функции y = f(x) с помощью сжатия к оси y с коэффициентом k. Отметим, что при этом точка пересечения графика с осью y остается на месте. Если же 0<k<1, то говорят о растяжении от оси y с коэффициентом 5) Зная график функции y = f(x), построить график функции y = f(k*x), ГДе k = -1 a. График функции y = f(-x) можно получить из графика функции y = f(x) путем преобразования симметрии относительно оси y. 6) Зная график y = f(x), построить график функции y = f(k*x), где k – отрицательное число. a. Построить график функции y = f(x) b. Осуществить его сжатие с коэффициентом |k| c. Сжатый график отобразить симметрично относительно оси y. Чтобы посмотреть примеры и получше все понять, смотрите параграф 13 учебника, 19 функция y=tg x y=ctg x их свойства и графики Свойство 1. Область определения функции у = tg х — множество всех действительных чисел, за исключением чисел вида
Первое представление о графике получено: он состоит из бесконечного множества ветвей (в полосе между Свойство 3. у =tg х—нечетная функция. Это следует из доказанного в § 5 соотношения Приступим к построению графика на полуинтервале
График функции у = tg х называют тангенсоидой. Ту ее часть, которая изображена на рис. 62, обычно называют главной ветвью тангенсоиды.
Свойство 6. У функции у = tg х нет ни наибольшего, ни наимень шего значения.
Замечание. Свойства 4—8, прочитанные по графику, можно доказать, опираясь на соответствующие математические утверждения, которые нам с вами пока не известны (поэтому мы и ограничиваемся наглядно-интуитивными представлениями). Впрочем, доказательство одного из свойств мы можем осуществить и сейчас.
20 Арккосинус. Решение уравнения cost = а
Определение. Если
21 Арксинус. Решение уравнения sint = a Определение.
Теперь мы в состоянии сделать общий вывод о решении уравнения t = a:
Билет 22 арктангенс и арккотангенс. Решение уравнений tg x=a, ctg x=a 23 билет
Однородные тригонометрические уравнения Уравнения вида a sin x+ b cos x= 0 называют однородными тригоном. уравнениями первой степени Алгоритм решения уравнений
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 471; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.62.51 (0.011 с.) |





















 . Например, если m=
. Например, если m=  , то говорят о сжатии с коэффициентом 3.
, то говорят о сжатии с коэффициентом 3. .
.

 нет точки, принадлежащей прямой
нет точки, принадлежащей прямой 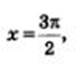 нет точки, принадлежащей прямой
нет точки, принадлежащей прямой  и т.д. Эти прямые проведены пунктиром на рис. 60.
и т.д. Эти прямые проведены пунктиром на рис. 60.
 полученного в § 5.
полученного в § 5. то затем нужно будет сдвинуть построенную ветвь по оси х вправо и влево на п, 2п, Зп и т.д. Тек самым получено второе представление о графике.
то затем нужно будет сдвинуть построенную ветвь по оси х вправо и влево на п, 2п, Зп и т.д. Тек самым получено второе представление о графике. График нечетной функции симметричен относительно начала координат. Значит, нам можно действовать так: построить по точкам часть графика на промежутке от
График нечетной функции симметричен относительно начала координат. Значит, нам можно действовать так: построить по точкам часть графика на промежутке от  а затем воспользоваться указанной симметрией.
а затем воспользоваться указанной симметрией. , Выберем контрольные точки:
, Выберем контрольные точки:

 В более общем виде — функция возрастает на любом интервале вида
В более общем виде — функция возрастает на любом интервале вида 
 функция претерпевает разрыв. Каждая прямая вида
функция претерпевает разрыв. Каждая прямая вида 
 . Возьмем два значения аргумента х1 и х2из этого промежутка: х1 < х2. Тогда в силу возрастания функции х на выбранном полуинтервале, будем иметь sin х1 < sin х2. В силу убывания функции у— соs х на выбранном полуинтервале будем иметь соs х1 > соs х2. Значит,
. Возьмем два значения аргумента х1 и х2из этого промежутка: х1 < х2. Тогда в силу возрастания функции х на выбранном полуинтервале, будем иметь sin х1 < sin х2. В силу убывания функции у— соs х на выбранном полуинтервале будем иметь соs х1 > соs х2. Значит,
 а это и означает возрастание функции у=tg х на выбранном промежутке.
а это и означает возрастание функции у=tg х на выбранном промежутке. то агссос а (арккосинус а) — это такое число из отрезка [0, п], косинус которого равен а (рис. 77). Итак,
то агссос а (арккосинус а) — это такое число из отрезка [0, п], косинус которого равен а (рис. 77). Итак,








