
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение длины отрезка прямой линии и углов наклона ее к плоскостям проекцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Величина отрезка прямой линии в пространстве выражается гипотенузой прямоугольного треугольника, один катет которого равен проекции отрезка на плоскость, а другой разности удалений концов отрезка от той же плоскости проекций (рис.12).
Истинная величина отрезка [АВ] определяется гипотенузой прямоугольного треугольника, у которого один катет [АВ0]=[А1В1], а второй ∆Z = ZВ - ZА. Угол φ определяется между отрезком [АВ] и горизонтальной проекцией [А1В1]= [АВ0]. Истинная величина отрезка определяется как гипотенуза прямоугольного треугольника, у которого один катет [АВ0]=[А1В1], а второй ∆Y = YВ - YА. Угол Ψ определяется между отрезком [АВ] и фронтальной проекцией [А2В2]= [АВ0]. Рассмотрим пример определения истинной величины отрезка [АВ] на эпюре (рис.13).
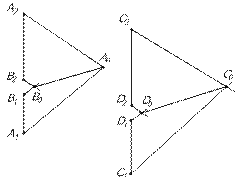
ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ ЛИНИЙ Если две прямые в пространстве параллельны, то и параллельны между собой одноименные проекции прямых. Если а ║ b, то а1 ║ b1, а2 ║ b2. Для того, чтобы судить о параллельности двух прямых общего положения в пространстве, необходима и достаточна параллельность их проекций на двух плоскостях проекций (рис.14). Параллельность профильных прямых не может быть определена по фронтальным и горизонтальным проекциям этой прямой. Для оценки их взаимного положения необходимо обратиться к профильной проекции, по которой и делают окончательный вывод (рис.15). Если [АВ]║[СD], то [А3В3]║[С3D3].
При безосной системе нужно сделать следующие построения (рис.16.). Применяя косоугольное проецирование строим А0В0 и С0D0.
[А1А0] ║ [В1В0] ║ [D1D0] ║ [С1С0] и [А2А0] ║ [В2В0] ║ [D2D0] ║ [С2С0].
Если [В0А0]║ [D0С0], то │АВ│ ║ │СD│
Пересекающиеся прямые. Пересекающиеся прямые имеют общую точку. Эта общая точка должна быть как в пространстве, так и на эпюре (рис.17). Если прямые пересекаются, то точки пересечения их одноименных проекций должны находиться на одной линии связи. a Для заключения о пересечении прямых общего положения достаточно иметь их проекции на две плоскости проекций. Если пересекаются профильные прямые, то необходимо построить их профильные проекции, а при безосной системе сделать дополнительные построения (рис.18).
Скрещивающиеся прямые.
Если прямые не пересекаются и не параллельны между собой, то точки пересечения их одноименных проекций не лежат на одной линии проекционной связи (рис.19). L и К – на одном перпендикуляре к М и N – на одном перпендикуляре к
ПРОЕКЦИИ ПЛОСКИХ УГЛОВ
Плоский угол проецируется на плоскость проекций в истинную величину тогда, когда обе его стороны параллельны плоскости проекций. Если стороны прямого угла произвольно расположены по отношению к плоскостям проекций, то прямой угол может проецироваться и тупым и острым. Если хотя бы одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость прямой угол спроецируется в виде прямого же угла (рис.20).
Пусть стороны АВ прямого угла АВС║
ЛЕКЦИЯ 3 ПЛОСКОСТЬ Положение плоскости в пространстве можно определить: 1. Тремя точками, не лежащими на одной прямой; 2. Прямой и точкой вне ее; 3. Двумя пересекающимися прямыми; 4. Двумя параллельными прямыми (рис.1).
Плоскость может быть задана также отсеками плоской фигуры (рис.2).
Возможны следующие положения плоскости относительно плоскостей проекций: 1.Плоскость, не перпендикулярная ни одной из плоскостей проекций, называется плоскостью общего положения (рис.1 и 2). 2. Частные положения плоскости: а) Плоскость, перпендикулярная к горизонтальной плоскости проекций Горизонтальные проекции всех точек и любых фигур, лежащих в горизонтально-проецирующей плоскости, совпадают со следом этой плоскости α1=
б) Плоскость, перпендикулярная к фронтальной плоскости проекций
Фронтальные проекции всех точек и фигур, лежащих в этой плоскости, совпадают с ее фронтальным следом. Угол φ между плоскостью
Плоскость, перпендикулярная к профильной плоскости проекций называется профильно-проецирующей плоскостью. Частный случай, когда профильно-проецирующая плоскость проходит через ось ОХ и делит пополам угол между плоскостями
Основные свойства проецирующих плоскостей состоят в том, что все геометрические образы, лежащие в них, на одной из плоскостей проекций изображаются прямой, совпадающей со следом плоскости, т.е. с линией пересечения проецирующей плоскости с соответствующей плоскостью проекций. Плоскости, перпендикулярные к двум плоскостям проекций, называется плоскостями уровня. Плоскость δ а) Плоскость δ, параллельная горизонтальной плоскости проекций
б) Плоскость
Любая фигура, расположенная в этой плоскости, проецируется на Все геометрические образы, расположенные в плоскостях, параллельных плоскостям проекций, проецируются на эти плоскости проекций без искажения. 3.2. ПРЯМАЯ И ТОЧКА В ПЛОСКОСТИ 1. Прямая принадлежит плоскости, если она имеет с этой плоскостью две общие точки (рис.8). 2. Прямая принадлежит плоскости, если она имеет с плоскостью одну общую точку и параллельна прямой, лежащей в этой плоскости (рис.9).
Построение точки в плоскости производится, исходя из условия, что она должна находиться на прямой, лежащей в этой плоскости. Т.о. задача на построение точки в плоскости сводится к задаче на построение прямой в этой плоскости (рис.10). Чтобы построить горизонтальную проекцию точки М, принадлежащей плоскости
3.3. ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ Главными линиями плоскости называются прямые, лежащие в данной плоскости и параллельные плоскостям проекций Линии наибольшего ската – прямые, проведенные по плоскости перпендикулярно к горизонталям (рис.12). Линия наибольшего ската и ее горизонтальная проекция образуют линейный угол, которым измеряется двугранный угол, составленный плоскостью С помощью главных линий плоскости оказывается удобным решать вопросы о взаимном расположении точки и плоскости (рис.13). Дана плоскость
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 996; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |


 <Ψ - угол наклона прямой к плоскости проекций
<Ψ - угол наклона прямой к плоскости проекций 



 b=K; a1
b=K; a1 



 ([ВВ1]∩[ВС]), но АВ║А1В1 – поэтому А1В1
([ВВ1]∩[ВС]), но АВ║А1В1 – поэтому А1В1 




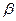 (a1 С)
(a1 С)
 (m ∩ n)
(m ∩ n)

 =
=  , который образуется между плоскостью
, который образуется между плоскостью 

 =
= 



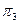 . Фронтальная и профильная проекция такой плоскости – горизонтальные прямые. Любая фигура, расположенная в плоскости δ2 на горизонтальную плоскость проекций проецируется без искажения.
. Фронтальная и профильная проекция такой плоскости – горизонтальные прямые. Любая фигура, расположенная в плоскости δ2 на горизонтальную плоскость проекций проецируется без искажения.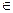 δ; А2В2С2
δ; А2В2С2  δ2; А1В1С1=АВС.
δ2; А1В1С1=АВС.













