
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение проекции МеркатораСодержание книги
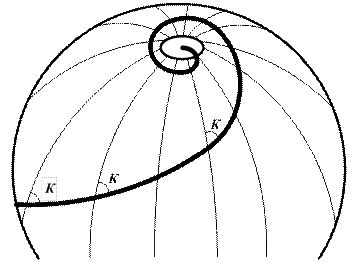
Поиск на нашем сайте Покажем, что прямая линия на карте в меркаторской проекции действительно представляет собой локсодромию. Локсодромия ® кривая, пересекающая все меридианы под одним и тем же углом К (рис. 6.2).
Рис. 6.2. Локсодромия на земном шаре
Судно, совершающее плавание постоянным курсом, перемещается именно по локсодромии. Уравнение локсодромии на поверхности эллипсоида имеет вид:
Если пренебречь сжатием эллипсоида и приняв Землю за шар, то уравнение локсодромии примет вид:
Из формулы (6.7) выводятся следующие свойства локсодромии: · – при К = 0°(180°) ® локсодромия совпадает с меридианом;
Длину и направление локсодромии по известным координатам точек вычисляют по формулам аналитического счисления. Напишем уравнение прямой, проходящей через т. А (Х0, У0) наклонно к оси Х под углом К равным курсу (рис. 6.3).
Рис. 6.3. Уравнение прямой
Подставим в полученное уравнение (6.5) вместо Х и У их выражения через j и l, принимая для простоты Землю за шар:
где а – коэффициент пропорциональности определяющий расстояния между меридианами.
Тогда:
Это уравнение показывает, что прямая линия на меркаторской проекции действительно представляет собой локсодромию. Таким образом, проводя на меркаторской проекции параллели в расстоянии МЧ от экватора, удовлетворяются оба требования, предъявляемые к морской навигационной карте. Единицы длины на карте меркаторской проекции Из принципа построения меркаторской проекции видно, что все параллели картографической сетки вытягиваются пропорционально secj и для сохранения равноугольности все меридианы этой сетки должны быть растянуты, в свою очередь, пропорционально растяжению параллелей, т.е. в secj раз. Чтобы построить картографическую сетку, удовлетворяющую требованию равноугольности, и учесть растяжение меридианов на величину secj надо практически знать удаление по меридианам каждой параллели от экватора. Удаление параллелей от экватора обычно выражается в экваториальных милях, так как экватор не испытывает растяжения и экваториальная миля ® величина const. Меридиональная часть (МЧ или D) ® расстояние по меридиану от экватора до данной параллели, выраженное в экваториальных милях. Если принимать Землю за шар, то МЧ вычисляется по формуле:
Для сфероида надо учесть сжатие Земли и формула для МЧ примет вид:
где а, в ® большая и малая полуоси земного эллипсоида. Вычисленные по формуле (6.13) МЧ для эллипсоида даны в табл. 26 «МТ-75» (с. 280¸287) в экваториальных милях с точностью до 0,1 по аргументу j с интервалом в 1¢ или в табл. 2.28 а «МТ-2000» (с. 314¸321) ® см. табл. 6.2.
Меридиональные части (выдержка) Таблица 6.2.
(более подробно см. табл. 24.5). Разность меридиональных частей (РМЧ) ® расстояние по меридиану на проекции Меркатора между двумя параллелями, выраженное в экваториальных милях. Меркаторская миля ® РМЧ двух параллелей, отстоящих друг от друга на 1¢. Меркаторская миля является изображением на карте морской мили для данной широты (j) и служит для измерения расстояний на карте. Длина меркаторской мили изменяется с широтой (j) пропорционально secj несмотря на то, что величина морской мили остается во всех широтах постоянной. Если в j = 0° меркаторская миля изображается отрезком, равным экваториальной миле, то в j = 60° она изобразится отрезком, равным 2-м экваториальным милям. То есть ® измерять расстояния на карте в проекции Меркатора по вертикальной рамке в той же средней широте, где лежит измеряемый отрезок. Единица карты ® длина изображения одной экваториальной мили на меркаторской карте, выраженная в линейных мерах (длина изображения 1′ дуги параллели в проекции Меркатора). Единица карты зависит от ее масштаба, который может быть отнесен к экватору или к любой выбранной параллели® главной параллели. ( см. табл. 6.1) Построение меркаторской карты начинается с вычисления единицы карты. Если СЭ ® главный масштаб по экватору, то единица карты (е) будет:
где Р 0 – длина 1′ дуги главной параллели (φ 0) в мм, (для φ 0 = 60о → Р 0 = 0,502.168 (из табл. 6.3) ´ 1852.000 = 930.015) С 0 – знаменатель главного масштаба карты; М 0 = 1/ С 0 – главный масштаб.
Длина минуты дуги меридиана и параллели (из табл. 2.29 «МТ-2000») Таблица 6.3.
Таблица 6.3 позволяет рассчитать для проекции Меркатора единицу карты (е), модули параллелей (υ), частные масштабы (М) и линейный масштаб карты (μ). Если при построении карты масштаб определяется тем условием, чтобы на карту поместился заданный район, то единица карты может быть рассчитана делением длины горизонтальной рамки карты (93 см или 68 см) на РД (D l) между крайними меридианами, выраженную в минутах. Таким образом, сущность построения меркаторской карты состоит в том, что меридианы проводятся на расстояниях, пропорциональных РД (D l), с учетом масштаба, а параллели – на расстояниях, пропорциональных РМЧ, с учетом того же масштаба. Как РД, так и РМЧ выражены при этом в одних и тех же постоянных единицах – экваториальных милях.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 934; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 (6.6)
(6.6)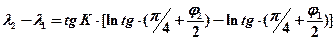 (6.7)
(6.7)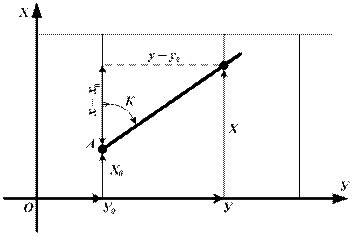
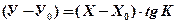 (6.8)
(6.8)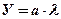 (6.9)
(6.9) (6.10)
(6.10) (6.11)
(6.11)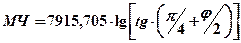 . (6.12)
. (6.12)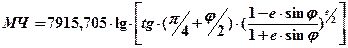 . (6.13)
. (6.13)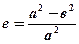 ® эксцентриситет эллипсоида вращения;
® эксцентриситет эллипсоида вращения; =
= 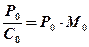 (6.14)
(6.14) 45
45
 62
62



