Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перспективные картографические проекцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Перспективные проекции применяются для составления некоторых справочных и вспомогательных карт (обзорные карты обширных районов, ортодромические карты, ледовые карты и пр.). Эти проекции представляют собой частный случай азимутальных проекций. (Азимутальные проекции – проекции, в которых меридианами являются радиальные прямые, исходящие из одной точки (центральной точки) под углами, равными соответствующим углам в натуре, а параллели – концентрические окружности, проведенные из точки схождения меридианов).
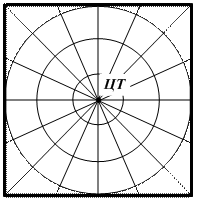
Рис. 10.3. Перспективные проекции В перспективных проекциях (рис. 10.3) поверхность Земли (сферы) переносится на картинную плоскость методом проецирования с помощью пучка прямых, исходящих из одной точки – точки зрения (ТЗ). Картинная плоскость может отстоять от поверхности сферы на некотором расстоянии (КП1), касаться сферы (КП2), или пересекать ее. Точка зрения (т. О) лежит в одной из точек на перпендикуляре к картинной плоскости, проходящем через центр сферы. Точку пересечения картинной плоскости с перпендикуляром называют центральной точкой карты (ЦТ). В зависимости от положения точки зрения (ТЗ) одна и та же точка (т. К0) будет отстоять на различных расстояниях r от ЦТ карты, что и будет определять характер искажений, присущих данной проекции. Наиболее распространенными перспективными проекциями являются – гномоническая (центральная) и стереографическая. В гномонической проекции точка зрения (ТЗ) совпадает с центром сферы (ТЗ ® в т. О1). Сетка меридианов и параллелей карты строится по формулам, связывающим прямоугольные координаты точек с их географическими координатами. В зависимости от положения центральной точки (ЦТ) карты, гномоническая проекция может быть (рис. 10.4): а) ® нормальной (полярной) – если центральная точка (ЦТ) совмещена с географическими полюсом (рис. 10.4 а); б) ® экваториальной (поперечной) – если центральная точка (ЦТ) расположена на экваторе (рис. 10.4 б); в) ® косой – если центральная точка (ЦТ) расположена в некоторой промежуточной широте (рис. 10.4 в).
Рис. 10.4. Гномонические проекции
Общие свойства карт в гномонической проекции: 1) ® большие искажения как формы, так и размеров фигур, возрастающие по мере удаления от центральной точки (ЦТ) карты, поэтому измерение расстояний и углов на такой карте затруднено. Измеряемые по карте углы и расстояния, называемые гномоническими, могут довольно значительно отличаться от истинных значений, вследствие чего для точных измерений карты в данной проекции не применяются; 2) ® отрезки дуги большого круга (ортодромии) изображаются прямыми линиями, что позволяет использовать гномоническую проекцию при построении ортодромических карт. Карты в гномонической проекции строятся, как правило, в мелких масштабах для участков поверхности Земли меньше полушария, а сжатие Земли не учитывается. В стереографической проекции картинная плоскость касается поверхности сферы, а точка зрения (ТЗ) расположена в т. О2 (рис. 10.3), являющейся антиподом точки касания. Эта проекция равноугольная, однако, для решения навигационных задач она неудобна, так как основные линии – локсодромия и ортодромия – изображаются в этой проекции сложными кривыми. Стереографическая проекция является одной из основных для построения справочных и обзорных карт обширных территорий. Равноугольная картографическая проекция Гаусса Общие положения Равноугольная проекция Гаусса применяется для составления топографических и речных карт, а также и планшетов. Основной картографической сеткой этой проекции является сетка прямоугольных координат. В прямоугольной системе координат проекции Гаусса вся поверхность земного эллипсоида разбита на 60 6-ти градусных зон, ограниченных меридианами, каждая из которых имеет свое начало координат – точку пересечения осевого меридиана зоны с экватором.
Рис. 10.5. Равноугольная проекция Гаусса
Счет зон введется от Гринвичского меридиана к Е от № 1 до № 60. Любую заданную точку в пределах зоны (т. А – рис. 10.5) получают в пересечении 2-х координатных линий: 1) ® дуги эллипса nAn ¢, параллельной осевому меридиану зоны и 2) ® кратчайшей линии АА ¢, проведенной из данной точки А перпендикулярно осевому меридиану. За начало координат в каждой зоне принимается точка пересечения осевого меридиана с экватором. Удаление точки А ¢ (основание перпендикуляра) от экватора определяется абсциссой Х, а удаление малого круга nn ¢ от осевого меридиана – ординатой У. Абсциссы Х во всех зонах отсчитываются в обе стороны от экватора («+» ® к N). Ординате У приписывается знак «плюс» (+), когда заданная точка удалена к Е (востоку) от осевого меридиана зоны, и знак «минус» (–), когда заданная точка удалена от осевого меридиана к W (западу). Для определения отечественного номера зоны, в которой расположена заданная точка с долготой l, применяют формулу:
(ближайшее целое число от 1 до 60). Деление долготы l производится до ближайшего целого числа (для l = 55° Е ® n = 10). Для вычисления долготы L0 осевого меридиана зоны применяют формулу:
(для n = 10 ® L0 = 57° Е). При западной долготе: l = 58° W ® l = 360° – 58° = 302° Е ® n = 51, а L0 = 303° Е или 57° W. N – международная нумерация зон (от меридиана 180° к востоку). Для Для В табл. 2.31 а «МТ-2000» указаны значения отечественных (n) и международных (N) номеров долготных зон, их границы и долгота ( Прямоугольная система координат применяется при производстве топографических работ, составлении топографических карт, расчете направлений и расстояний между точками при малых расстояниях. Граничными линиями карты в проекции Гаусса служат меридианы и параллели. Положение заданной точки на карте определяют указанием плоских прямоугольных координат Х и У. Этим координатам соответствуют километровые линии: Х = const – параллельна экватору, и У = const – параллельная осевому меридиану зоны. Плоские координаты Х и У являются функциями географических координат точки и в общем виде могут быть представлены выражениями:
где l – разность долгот заданной точки и осевого меридиана, т.е.
Вид функций f1 и f 2 выводится так, чтобы обеспечивалось свойство равноугольности проекции при постоянном масштабе вдоль осевого меридиана зоны. Километровые линии – линии одинаковых значений абсцисс X = const или ординат Y = const, выраженные целым числом км. Километровые линии (X = const и У = const) ® два семейства взаимно перпендикулярных прямых и оцифровываются соответствующими значениями координат в км. На картах в проекции Меркатора линии X изображаются кривыми, обращенными выпуклостью к полюсу, а линии Y – кривыми, выпуклостью к осевому меридиану и расходящимся по мере удаления от экватора. Для исключения отрицательных значений ординат оцифровка осевого меридиана увеличена на 500 км. (При Х = 6656 и У = 23612 ® заданная точка удалена от экватора по осевому меридиану на 6656 км, находится в 23-й зоне и имеет условную ординату 612, а фактически ® 112 км к Е). Прямоугольные координаты Х и У выражают обычно в метрах. Рамки карт в проекции Гаусса разбиты на минуты по широте и долготе. Значения широт и долгот параллелей и меридианов, ограничивающих карту, надписываются в углах рамки. Меридианы и параллели на карту не наносятся. При необходимости их можно провести через соответствующие деления минут широты и долготы на рамках карты. Угол между километровой линией У = const и истинным меридианом называется сближением или схождением меридианов. Этот угол (Ð g) отсчитывается от северной части истинного меридиана по часовой стрелке до северной части километровой линии У = const (см. рис. 10.6). Схождению меридианов приписывают знак «плюс» (+), если заданная точка расположена к Е (востоку) от осевого меридиана, и знак «минус» (–), если она расположена к W (западу) от осевого меридиана зоны. При известных координатах j и l заданной точки угол g вычисляется по формуле:
где L0 – долгота осевого меридиана зоны. Пример: для точки j = 56°20¢ N; l = 124°51¢ E: n = 21 L0 = 123° E и g = +1°32,4¢. Ввиду ограниченной ширины зоны кратчайшие линии на картах в проекции Гаусса, изображаются практически прямыми линиями, а масштаб по всей карте постоянен. Эти свойства, а также наличие сетки прямоугольных координат являются главными причинами широкого применения данной проекции при всех топографических, геодезических и гидрографических работах. Для решения задач, связанных с использованием как географических, так и прямоугольных координат точек, а также с прокладкой отрезков локсодромий, применяются карты, составленные в нормальной проекции Меркатора с дополнительно нанесенной сеткой прямоугольных координат Гаусса. Основные свойства таких карт полностью соответствуют таковым для нормальной проекции Меркатора.
Планшеты в проекции Гаусса Планшеты в проекции Гаусса составляют в крупных масштабах (от 1:50.000). Границами планшета являются километровые линии, координаты которых: XS, XN, УЕ, УW пишут вдоль линий. На рамках планшета наносят выходы километровых линий, соответствующих целому числу км. Для прокладки курсов и пеленгов на планшетах проводят несколько истинных меридианов через 10¸15¢ по долготе. Линии курсов прокладывают, отсчитывая углы от ближайших к месту судна, меридианов, а линии пеленгов – от меридианов (ближайших) тех точек, в которых измерялись пеленги. Для прокладки пройденных судном расстояний вблизи одной из боковых рамок строится шкала стандартных морских миль (или S переводится в км). Направления на картах или планшетах в проекции Гаусса часто определяют относительно километровых линий. Угол между северной частью километровой линии У = const и направлением заданной прямой – дирекционный угол a. Счет a ведется по круговой системе. При известном дирекционном угле истинный пеленг (ИП) рассчитывается (рис. 10.6):
Пример: в точке j = 50°35¢ N; l = 66°10¢ E измерен a = 156,2°. ИП =? Решение: 1) 2) 3) 4)
Рис. 10.6. Дирекционный угол
Применение прямоугольной системы координат упрощает решение прямой и обратной геодезических задач. Прямая геодезическая задача – вычисление координат искомой точки (т. Е2) по известным координатам Х1, У1 исходной точки (т. Е1), дирекционному углу a и расстоянию (базе) Е1Е2 = Б.
® знаки приращений D Х и D У совпадают со знаками функций cos a и sin a. Если задан ИП или азимут АБ, то:
Обратная геодезическая задача – вычисление направления и расстояния между точками по известным их координатам.
а Координаты точек должны быть даны в одной и той же координатной зоне.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 936; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |


 а)
а)
 б)
б)
 в)
в)

 (10.16)
(10.16) (10.17)
(10.17) : N = n + 30 и n = N – 30 (для восточного полушария).
: N = n + 30 и n = N – 30 (для восточного полушария). : N = n – 30 и n = N + 30 (для западного полушария).
: N = n – 30 и n = N + 30 (для западного полушария). ) осевого меридиана ® см. табл. 10.1.
) осевого меридиана ® см. табл. 10.1. (10.18)
(10.18) (10.19)
(10.19) (10.20)
(10.20) (10.21)
(10.21)
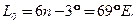
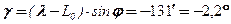 .
. .
.
 (10.22)
(10.22)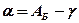 , (g – для т. Е1). (10.23)
, (g – для т. Е1). (10.23) , (10.24)
, (10.24) . (10.25)
. (10.25)