Классификация плоских проекций.

Перед разработчиками информационных систем, использующих средства пространственного моделирования, встает задача преобразования трехмерных объектов и сцен, состоящих из них, для представления на плоских поверхностях устройств изображения, т.е. задача перехода из трехмерного пространства на плоскость. Процесс перехода с трехмерного пространства на плоскость не является однозначным, т.е. для одного трехмерного объекта возможно множество двумерных проекций. В начертательной геометрии и черчении различают следующие проекции:

• перспективная, которая находит широкое применение в живописи, архитектуре

• параллельная, использующаяся в основном в технических приложениях.

Однако в последнее время и средства технического проектирования стали ориентироваться на более реалистичные перспективные проекции.

При построении перспективной проекции выбирается один или несколько центров проецирования, после чего определяются точки пересечения плоскости проецирования с лучами проецирования – прямыми, исходящими из центра проецирования.

Перспективное (центральное) проецирование можно рассматривать как наиболее общий случай (рис.2.11). Причем его можно разложить на два преобразования:

• перспективное преобразование, осуществляющее переход из двумерного пространства в перспективное

• двумерное проецирование, осуществляющее переход из двумерного пространства в двумерную плоскость

Параллельное проецирование (рис.2.12) можно рассматривать как частный случай перспективного проецирования, при котором центр проецирования удален в бесконечность. При этом лучи проецирования становятся параллельными друг другу.

Параллельная проекция называется аксонометрической в том случае, если линии проецирования перпендикулярны плоскости проецирования. В противном случае проекции называются косоугольными.

В практике технического проектирования наиболее распространены аксонометрические проекции, среди которых различают четыре вида.

1. Прямоугольные (ортогональные) – проекции, у которых плоскости проецирования параллельны координатным плоскостям. Частным случаем ортогональной проекции, при которой плоскости проецирования совпадают с координатными плоскостями, является ортографическая проекция

2. Изометрическая проекция (изометрия) – это проекция, для которой предполагается одинаковое масштабирование по всем трем осям. Следствием этого является равенство всех углов между проекциями координатных осей

3. Диметрическая проекция (диметрия) – проекция, у которой масштаб по одной из осей координат выбран вдвое меньше, чем по двум другим.

4. Триметрическая проекция (триметрия) – не накладывает никаких ограничений на масштабирование осей, следствием чего является произвольное расположение проекций координатных осей на плоскости проецирования.

Конец 9 вопроса.

Ортографическая проекция

При их построении используется аппарат аффинной геометрии. Аффинные преобразования представляют собой замкнутую систему линейных преобразований, результат которых также является аффинным.

С формальной точки зрения аффинные преобразования определяются матрицей преобразований Т, в которой четвертый столбец имеет вид: 0001

Среди аксонометрических проекций различают прямоугольную, диметрическую, изометрическую и триметрическую проекции.

Общий вид матрицы преобразований для получения прямоугольной (ортографической) проекции следующий:

При этом два из трёх диагональных элементов (а, е, i) равны единице, а третий должен быть нулевым. Например, ортографическая проекция на плоскость XOY (Z=0) определяется следующей матрицей преобразований:

Ортогональные проекции являются частным случаем прямоугольной проекции, при котором проецирование осуществляется на координатные плоскости. Для выполнения ортогональных построений необходимо сместить плоскость проецирования параллельно одной из координатных плоскостей. Например, матрица преобразований для построения ортогональной проекции на плоскость Z=P будет иметь вид:

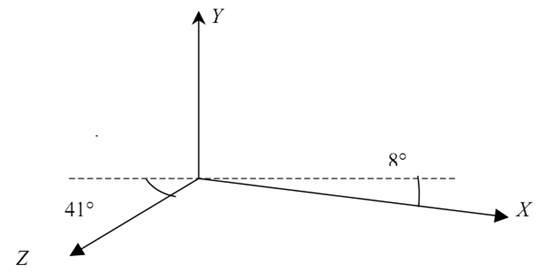
Таким образом, ортогональное или прямоугольное проецирование определяется матрицей преобразований с нулевой строкой, соответствующей той оси, перпендикулярно которой находится плоскость проецирования.

Ортогональные и ортографические проекции находят широкое применение в техническом черчении. Совокупность двух или трех ортографических проекций называется эпюром Монжа. При построении эпюра Монжа возможно использование двух систем расположения плоскостей и проекций:

• правая система, принятая в России и в Европе,

• левая система, используемая на американском континенте.

Эпюр Монжа представляется в виде трех проекций:

• Пф - фронтальная проекция;

• Пп - профильная проекция;

• Пг - горизонтальная проекция.

На эпюре Монжа (рис.2.15) изображён геометрический объект,расположенный в 1-м квадранте правой системы. Расположение и направление осей определяется следующим образом:

• в правой системе: ось OX - влево, ось OY - к зрителю, ось OZ - вверх;

• в левой системе: ось OX - вправо, ось OY - вверх, ось OZ - к зрителю.

Конец 10 вопроса.
11. Геометрические построения в диметрической проекции.

Для построения более сложных аксонометрических проекций необходимо использовать комбинацию преобразований поворотов и проекций из бесконечности. Рассмотрим пример проецирования на плоскость Z = 0 (Рис.2.16).

Для построения диметрии необходимо, чтобы масштаб по осям ОX и ОY были равны 1:1, а по оси OZ - 1:2. Рассмотрим единичные векторы ex, ey и ez, расположенные в исходном трёхмерном пространстве. В системе однородных координат их величины будут выглядеть следующим образом:

 

Конец 11 вопроса.
12. Геометрические построения в изометрической проекции.

Последний вид аксонометрической проекции - триметрическая проекция - не ограничена каким-либо соотношением по координатным осям, поэтому для её построения в любом случае нужно производить самостоятельные расчёты углов поворота и матриц преобразований Т, аналогично тому, как это было сделано для диметрии и изометрии.

Конец 12 вопроса.

Косоугольные проекции.

Косоугольные проекции отличаются от аксонометрических тем, что угол образуемый лучом проецирования с плоскостью проецирования не равен 90°. При выполнении преобразований в данной системе проекций следует помнить, что ортогональность системы координат не сохраняется, и данные преобразования будут приводить к не корректному результату. Среди множества косоугольных проекций наибольшее распространение получили два варианта:

1. Свободная проекция (проекция Кавалье). У этой проекции две оси взаимно перпендикулярны и имеют масштаб 1:1, третья ось наклонена к горизонтали, но так же имеет масштаб 1:1, при этом угол между лучами проецирования и плоскостью проекции равен 45°.

2. Кабинетная проекция (проекция Кабинэ). Представляют собой частный случай свободной проекции, в которой масштаб по третьей оси составляет 1:2.

Конец 13 вопроса.