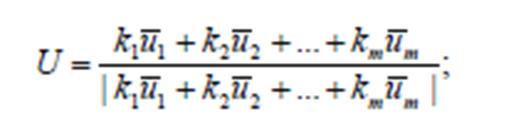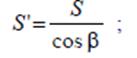Графические данные и их классификация.

Пространственное вращение вокруг произвольной оси.

Пространственное вращение вокруг произвольной оси. Данную операцию можно в какой-то мере считать универсальной и на ее базе реализовывать все остальные операции в пространстве. Так эта операция не относится к элементарным, ее следует разложить на простейшие. Из них в данном случае потребуются операции переноса и вращения вокруг осей координат. Для того чтобы свести операцию вращения вокруг произвольной оси к эти операциям, необходимо выполнить следующие действия:

• перенести исходную ось вращения таким образом, чтобы она проходила через начало системы координат.

• повернуть перемещаемую ось до совпадения с одной из координатных плоскостей

• в пределах выбранной координатной плоскости осуществить плоский поворот до совпадения с одной из координатных осей

• теперь можно выполнить заданный поворот вокруг оси, которая совмещена с одной из осей координат

• повторение действий в обратном порядке

Рассмотрим поворот на угол γ вокруг произвольной оси. Для этого необходимо выполнить следующие семь шагов:

1. Перенос оси вращения в начало системы координат.

2. Поворот на угол α относительно оси ОХ до пересечения с плоскостью XOZ

3. Поворот на угол β в плоскости XOZ до совмещения с осью OZ

4. Поворот на угол γ вокруг оси OZ

5. Поворот на угол - β вокруг OY

6. Поворот на угол - α вокруг ОХ

7. Перенос оси вращения на прежнее место

Рассмотрим математическое описание данных действий в матричном виде. Будем описывать все производимые действия в виде вложенных преобразований конгруэнтности.

1. Преобразование переноса (прямое и обратное):

2. Поворот на угол α относительно ОХ:

3. Поворот на угол β относительно OY до совмещения с осью OZ:

 

4. Поворот на угол γ:

 

Полное преобразование, описывающее поворот в пространстве вокруг произвольной оси:

Конец 8 вопроса.

Конец 9 вопроса.

Ортографическая проекция

При их построении используется аппарат аффинной геометрии. Аффинные преобразования представляют собой замкнутую систему линейных преобразований, результат которых также является аффинным.

С формальной точки зрения аффинные преобразования определяются матрицей преобразований Т, в которой четвертый столбец имеет вид: 0001

Среди аксонометрических проекций различают прямоугольную, диметрическую, изометрическую и триметрическую проекции.

Общий вид матрицы преобразований для получения прямоугольной (ортографической) проекции следующий:

При этом два из трёх диагональных элементов (а, е, i) равны единице, а третий должен быть нулевым. Например, ортографическая проекция на плоскость XOY (Z=0) определяется следующей матрицей преобразований:

Ортогональные проекции являются частным случаем прямоугольной проекции, при котором проецирование осуществляется на координатные плоскости. Для выполнения ортогональных построений необходимо сместить плоскость проецирования параллельно одной из координатных плоскостей. Например, матрица преобразований для построения ортогональной проекции на плоскость Z=P будет иметь вид:

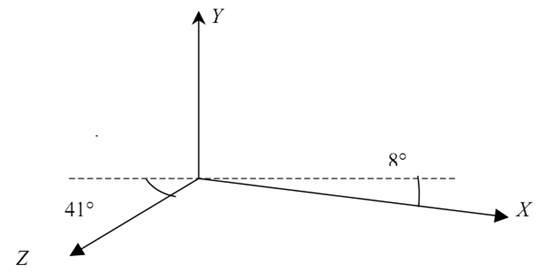
Таким образом, ортогональное или прямоугольное проецирование определяется матрицей преобразований с нулевой строкой, соответствующей той оси, перпендикулярно которой находится плоскость проецирования.

Ортогональные и ортографические проекции находят широкое применение в техническом черчении. Совокупность двух или трех ортографических проекций называется эпюром Монжа. При построении эпюра Монжа возможно использование двух систем расположения плоскостей и проекций:

• правая система, принятая в России и в Европе,

• левая система, используемая на американском континенте.

Эпюр Монжа представляется в виде трех проекций:

• Пф - фронтальная проекция;

• Пп - профильная проекция;

• Пг - горизонтальная проекция.

На эпюре Монжа (рис.2.15) изображён геометрический объект,расположенный в 1-м квадранте правой системы. Расположение и направление осей определяется следующим образом:

• в правой системе: ось OX - влево, ось OY - к зрителю, ось OZ - вверх;

• в левой системе: ось OX - вправо, ось OY - вверх, ось OZ - к зрителю.

Конец 10 вопроса.
11. Геометрические построения в диметрической проекции.

Для построения более сложных аксонометрических проекций необходимо использовать комбинацию преобразований поворотов и проекций из бесконечности. Рассмотрим пример проецирования на плоскость Z = 0 (Рис.2.16).

Для построения диметрии необходимо, чтобы масштаб по осям ОX и ОY были равны 1:1, а по оси OZ - 1:2. Рассмотрим единичные векторы ex, ey и ez, расположенные в исходном трёхмерном пространстве. В системе однородных координат их величины будут выглядеть следующим образом:

 

Конец 11 вопроса.
12. Геометрические построения в изометрической проекции.

Последний вид аксонометрической проекции - триметрическая проекция - не ограничена каким-либо соотношением по координатным осям, поэтому для её построения в любом случае нужно производить самостоятельные расчёты углов поворота и матриц преобразований Т, аналогично тому, как это было сделано для диметрии и изометрии.

Конец 12 вопроса.

Косоугольные проекции.

Косоугольные проекции отличаются от аксонометрических тем, что угол образуемый лучом проецирования с плоскостью проецирования не равен 90°. При выполнении преобразований в данной системе проекций следует помнить, что ортогональность системы координат не сохраняется, и данные преобразования будут приводить к не корректному результату. Среди множества косоугольных проекций наибольшее распространение получили два варианта:

1. Свободная проекция (проекция Кавалье). У этой проекции две оси взаимно перпендикулярны и имеют масштаб 1:1, третья ось наклонена к горизонтали, но так же имеет масштаб 1:1, при этом угол между лучами проецирования и плоскостью проекции равен 45°.

2. Кабинетная проекция (проекция Кабинэ). Представляют собой частный случай свободной проекции, в которой масштаб по третьей оси составляет 1:2.

Конец 13 вопроса.

Конец 17 вопроса.

 

Стереографическая проекция — центральная проекция, отображающая двумерную сферу (с одной выколотой точкой) на плоскость.

Плоскость касается сферы в некоторой точке, центром проекции является точка, диаметрально противоположная. Через каждую точку А сферы проходит единственная прямая, соедининяющая А и центр проекции. Эта прямая пересекает плоскость в единственной точке, которая, таким образом, является образом точки А при стереографической проекции. В результате получается взаимно однозначное отображение сферы с выколотым центром проекции на плоскость.

Для того, чтобы получить взаимно однозначное отображение целой сферы, нужно дополнить плоскость элементом, являющимся образом выколотой точки центра проекции. Этот элемент — так называемая бесконечно удалённая точка, обозначаемая символом бесконечности. Плоскость, дополненная элементом, называется расширенной плоскостью.

Свойства проекции

Стереографическая проекция является конформным отображением — она сохраняет углы между кривыми и форму бесконечно малых фигур. Стереографическая проекция переводит окружности на плоскости в окружности на сфере, а прямые на плоскости — в окружности, проходящие через центр проекции O'.

Стереографическая проекция отображает сопряжённые пучки меридианов и параллелей на сфере в сопряжённые эллиптический и гиперболический пучки окружностей на плоскости.

Стереографическая проекция осуществляет гомеоморфизм комплексной проективной прямой на двумерную сферу: для этого нужно рассмотреть двумерную вещественную плоскость с координатами x,y как одномерную прямую комплексного переменного z = x + iy.

Стереографическая проекция используется для отображения сферических панорам в фоотографии. Это приводит к интересным результатам: области, удалённые от центра проекции, сильно растягиваются, производя так называемые «эффекты маленькой планеты». В сравнении с другими азимутальными проекциями, стереографическая обычно производит самые приятные на вид панорамы; это связано с точной передачей форм в результате конформности проекции.

 

 

Конец 42 вопроса.

Конец 49 вопроса.

 

 

50.Абстрактные цветовые модели CIE XYZ и CIE L*a*b*.

Рассмотренные выше группы пространственных цветовых моделей

напрямую связаны либо с характеристиками аппаратных средств, либо

с физиологическими или психологическими особенностями восприятия цвета человеком.

Среди абстрактных моделей, разработанных Международным Комитетом по Освещению (МКО) CIE1, в настоящее время используются модели CIE XYZ, CIE L*a*b*,

CIE L*u*v*, CIE L*с*h*. С целью устранения зависимости цветовых характеристик от субъективных факторов, международный комитет в конце 20-х годов начал работу по созданию абстрактной цветовой модели, позволяющей объективно оценить цветовые характеристики источников света и отражающих объектов. Первый стандарт на абстрактное цветовое пространство был принят в 1931-м году и носит название

CIE XYZ 1931.

Определение цвета в этой системе не связано с цветами, воспринимаемыми человеком, или с цветами, воспроизводимыми аппаратными средствами. При этом координата Y задается таким образом, чтобы ее распределение энергии совпадало с кривой чувствительности глаза человека (суммарная кривая на рис.5.1).

Пусть X, Y и Z – веса основных цветов CIE. Однако на практике удобней использовать относительные показатели цветности:Легко заметить, что x + y + z = 1. Поэтому на практике используются только два относительных показателя - x и y (z = 1 - x – y). Для

однозначного определения положения в трехмерном цветовом пространстве дополнительно используется координата Y. Широко известен цветовой график МКО который представляет собой проекцию пространства (x, y, Y) при Y= const. На границе области располагаются спектрально чистые (хроматичекие) цвета, а внутри – все видимые цвета. При этом все цвета, имеющие одинаковую цветность (x, y), но различную яркость, отображаются в одну точку графика МКО. При построении модели CIE XYZ разработчики хотели добиться 100%-чистого цвета постоянной яркости по всей длине видимого

спектра. В результате этого при пересчете XYZ- цветов в RGB -модель получались отрицательные значения Это означает, что не все цвета представимы в RGB-

пространстве. Внутри области МКО лежит кривая, соответствующая цветам абсолютно черного тела, на которой находятся стандартные точки МКО (точки A, B, C, D, E на рис.5.9). Стандартные точки соответствуют следующим величинам:

1) точка А (0.448;0,408) – цвет газонаполненной лампы накаливания с вольфрамовой нитью при 2850°К;

2) точка В (0.349;0,352) – солнечный свет в полдень (4800°К);

3) точка С (0.310;0,316) – полуденный свет при сплошной облач-

ности (6500°К);

4) точка D (0.313;0,329) – опорный цвет телевизионных систем

(6500°К);

5) точка E (0.333;0,333) – точка равных энергий (5700°К) в кото-

рой значения координат равны (x = y = z = 1/3).

Используя график МКО можно определять цвет дополнительный к заданному и доминирующий цвет светового потока. Для определения доминирующего цвета (доминирующей длины волны) следует соединить прямой линией точку заданного цвета и опорного белого, а затем продолжить до пересечения с границей области МКО. Чтобы определить дополнительный цвет, необходимо провести прямую через точки заданного цвета и точку опорного белого цвета и продолжить ее до пересечения с противоположной границей области.Недостатком модели CIE XYZ является то, что цветовое пространство этой модели является неоднородным, что затрудняет операции с цветами (величина разности двух цветов зависит от положения точек в пространстве). Для устранения этого и некоторых других недостатков старой системы в 1976 году был разработан новый стандарт

CIE L*a*b*. Координатами в данном цветовом пространстве являются:

L* – светлота;

а* – цвета от зеленого до красного;

b* – цвета от синего до желтого.

Пространство CIE L*a*b* ограничено сферой (рис.5.11). Параметры пространства рассчитаны на среднего стандартного наблюдателя. Определенной разнице координат двух точек в этом пространстве(двух цветов) можно поставить в соответствие среднеквадратичное отклонение:

Величина Δ E может служить оценкой качества изображения. В стандарте CIE L*a*b* определена градация Δ E, определяющее качествоизображения:

< 0.2 - незаметное отличие;

0.2 ÷ 0.5 - очень

незначительное;

0.5 ÷1.5 - незначительное;

1.5 ÷ 3 - отчетливое;

3 ÷ 6 - очень отчетливое;

6 ÷12 - сильное;

> 12 - очень сильное.

Данная система цветовых координат широко используется в до-

печатной подготовке цветных оттисков, т. к. позволяет выполнять коррекцию цвета, не изменяя соотношения цветов.

Конец 50 вопроса.

Гамма-коррекция — коррекция яркости цифрового изображения с помощью степеннóй функции. Гамма-коррекция позволяет:

приспособить изображение под устройство ввода-вывода с нелинейной яркостной характеристикой;

повысить контрастность, разборчивость тёмных участков изображения, не делая при этом чрезмерно контрастными или яркими светлые детали снимка.

Пример гамма-коррекции изображения на ЭЛТ.

Демонстрация гамма-коррекции изображения. Значения γ от 0,5 до 4 от исходного изображения (γ=1).

Значение γ=1 соответствует «идеальному» монитору, который имеет линейную зависимость отображения от белого к чёрному. Но таких мониторов не бывает — зависимость, в особенности для электронно-лучевых устройств, нелинейна. Большее значение гаммы означает более высокую нелинейность этой зависимости. Стандартное значение гаммы для стандарта видеоизображений NTSC — 2.2. Для дисплеев компьютера значение гаммы обычно составляет значения от 1.5 до 2

Математическая формула гамма-коррекции

Информация о яркости в аналоговом виде в телевидении, а также в цифровом виде в большинстве распространённых графических форматов, хранится в нелинейной шкале. Яркость пиксела на экране монитора, в первом приближении, можно считать пропорциональной

где I — яркость пиксела на экране дисплея (или яркости составляющих цвета, красной, зелёной и синей по отдельности), V — численное значение цвета от 0 до 1, а γ — показатель гамма-коррекции.

Исторически это обусловлено тем, что у электронно-лучевой трубки зависимость между количеством испускаемых фотонов и напряжением на катоде близка к формуле (1). Для жидкокристаллических мониторов, проекторов и т. д., где зависимость между напряжением и яркостью имеет более сложный характер, используются специальные компенсационные схемы.

При переносе графического файла между компьютерами копия изображения может выглядеть светлее или темнее, чем оригинал. Ситуация усложняется, если на компьютерах установлены различные операционные системы (например Microsoft Windows и GNU/Linux), или когда машины построены на базе разных аппаратных платформ (например, IBM PC и Macintosh).

Например, встроенная в формат PNG гамма-коррекция работает следующим образом: данные о настройках дисплея, видеоплаты и программного обеспечения (информация о гамме) сохраняется в файле вместе с самим изображением, что и обеспечивает идентичность копии оригиналу при переносе на другой компьютер.

Исправление гамма-коррекции фотоснимка

Если фотоснимок выглядит слишком темным или блеклым, попробуйте произвести его гамма-коррекцию. Помимо профессиональных средств обработки изображений эту возможность поддерживает, например, компактная программа просмотра изображений IrfanView.[3]

Проявление скрытых особенностей изображения

Гамма-коррекция позволяет проявить скрытые особенности полутонового изображения, показав в более четком виде скрытые тенью полутоновые переходы в его тёмной области. В частности, такие особенности в ряде случаев удается выявить на лунных снимках НАСА (подробнее...).[4]

Повышение контрастности печатного текста

Если буквы в отсканированном тексте выглядят слишком блёклыми и имеют недостаточную черноту, понижение (например до 0.5) показателя гамма-коррекции изображения увеличит контрастность букв на фоне бумаги. Понижение гамма-коррекции по сравнению с простым повышением контрастности позволяет увеличить «черноту» отпечатанных символов, но при этом не проявить дефекты бумаги (которые являются оттенками более светлых тонов).
Цветова́я температу́ра (спектрофотометрическая или колориметрическая температура; обозначается Тс) — характеристика хода интенсивности излучения источника света как функции длины волны в оптическом диапазоне. Согласно формуле Планка цветовая температура определяется как температура абсолютно чёрного тела, при которой оно испускает излучение того же цветового тона, что и рассматриваемое излучение. Характеризует относительный вклад излучения данного цвета в излучение источника, видимый цвет источника. Применяется в колориметрии, астрофизике

Применение

Цветовая температура источника света:

характеризует спектральный состав излучения источника света,

является основой объективности впечатления от цвета отражающих объектов и источников света.

По этим причинам она определяет ощущаемый глазом цвет предметов при наблюдении в данном свете (психология восприятия цвета).

В связи с тем, что цвет объекта зависит и от его собственных спектральных свойств, и от характера освещения, в технике стандартизуют наиболее распространённые источники света прежде всего по цветовой температуре.

Стандартные источники

Так, источник Д65 с цветовой температурой 6500 К имеет в своём спектре существенную ультрафиолетовую составляющую. Хотя человеческий глаз не воспринимает ультрафиолетовых лучей, многие объекты (в т. ч. красители) способны светиться под их действием.

Вот почему возникла необходимость в стандартизации УФ-составляющей для источников, имитирующих дневной свет (Д65) — ведь, например, без УФ-компоненты бумага будет не такой белой (в неё вводят белофоры), а реклама — не такой яркой (в ней часто используют люминесцирующие красители). Благодаря белофорам белизна современной бумаги может превышать 100 %.

Цветовая температура в фотографии, кинематографе и телевидении

Цветная фотоплёнка выпускается для определённых фиксированных цветовых температур источника света. Негативная и Слайдовая плёнка выпускались сбалансированными для съемки при дневном (5600К) свете или при свете ламп накаливания (3200К) - "вечерняя" пленка. Это позволяет получать сбалансированное по цвету изображение при различных источниках освещения без применения конверсионных фильтров и цветокоррекции. С появлением маскированных негативных цветных пленок, они стали выпускаться сбалансированными под промежуточную цветовую температуру - 4500К вследствие неизбежности цветокоррекции в процессе печати позитивного изображения. Таким образом, негативная пленка пригодна для съемки при любом освещении, давая изображение, требующее незначительной коррекции. При съемке на обращаемую пленку исправление готового изображения невозможно. Поэтому пленка для слайдов должна быть сбалансирована для реальных источников света. При профессиональной съемке слайдов для полиграфии применялись специальные приборы[1] для измерения цветовой температуры освещения (цветомеры) и конверсионные светофильтры. При профессиональной киносъемке эти же технологии применялись даже при съемке на негативную кинопленку. В цифровых фотоаппаратах и видеокамерах используется автоматическое определение цветовой температуры или ее предустановки в зависимости от сюжета съёмки. В цифровой фотографии и телевидении эта настройка называется "баланс белого". В некоторых случаях цветовую температуру можно переопределить при дальнейшей обработке цифрового снимка или видеозаписи, однако в большинстве случаев это ведет к потере качества цветопередачи. Изменение баланса белого без потерь качества возможно при записи несжатого фото- и видеоизображения - RAW. Последнее широко применяется в цифровом кинематографе.

 

 

Модель закраски Фонга.

Данный метод превосходит метод Гуро по объемам вычислений, однако позволяет добиться более высокого качества сглаживания полигональных поверхностей.

Метод Фонга (Phong Shading) также базируется на линейной интерполяции. Однако в качестве интерполируемой величины выступает не интенсивности точек поверхности, а векторы нормалей к поверхности в этих точках.

Метод Фонга заключается в построении для каждой точки поверхности вектора-нормали G U. На базе полученного значения G U производится вычисление интенсивности 0 I. Схема интерполяции аналогична схеме, приведенной для метода Гуро. При этом нормали в вершинах полигональной сетки определяется как сумма нормалей прилегающих гра-

ней:

где i k - коэффициент, определяющий вес грани среди всех граней, которые имеют общую вершину.

Для вычисления нормали G U, используются значения векторов

Для расчета значений интенсивности, используются формулы закраски, в которых вместо углов α и β используются векторы-нормали по соответствующим направлениям. Благодаря этому, метод Фонга поzволяет получить более реалистичный эффект сглаживания, позволяющий учитывать зеркальную составляющую отраженного света.

Достоинства метода Фонга:

- гарантированная гладкость изменения интенсивности;

- в большинстве случаев устраняет эффект Маха, присущий методу Гуро;

- обеспечивает высокое быстродействие за счет наличия рекурсии в вычислениях.

Недостатки метода Фонга:

- возможны ошибки при вычислении большого числа невыпуклых многоугольников;

- не исключена возможность появления полос Маха (например,для сфер эффект Маха усиливается).

Конец 61 вопроса.

 

 

Алгоритм отсечения лучей.

Алгоритм отсечения лучей (Ray Casting) является простейшим вариантом алгоритмов обеспечивающих виртуальную реальность. Наиболее известно использование этого алгоритма в качестве графического ядра первых 3D игровых программ.

 

 

Алгоритм отсечения лучей(АОЛ) можно рассматривать как упрощенный вариант алгоритма трассировки лучей с обратным ходом луча. Для упрощения реализации вычислительных функций данный алгоритм рассматривает простейшую геометрическую модель пространства в виде конечного числа кубов.Идея АОЛ заключается в том, что при построении каждого очередного кадра по направлению взгляда наблюдателя в этом пространстве отсекается сектор лучей (600-900). Все остальные лучи, выходящие за поле

просмотра, не рассматриваются, то есть отсекаются. В алгоритме не учитываются источники света и отражательные характеристики поверхности объекта. Учет освещенности производится статически, то есть описывается на старших формированиях пространства, и в момент выполнения алгоритма находится в описании кубов, из которых

сформировано объектное пространство.Динамические объекты сцены (движущиеся персонажи) реализованы в виде спрайтов1. Поэтому данное графическое ядро

относят к 2,5D графическим программам. После выделения сектора просмотра вычисляются координаты точек пересечения лучей с объектами пространства. Причем

лучи проводятся через каждый пиксель экрана.

1 Под спрайтом понимают семейство растровых изображений, отображающих фазы движения какого-либо объекта. Спрайт используется для формирования анимационных последовательностей в игровых и мультимедийных программах

Взгляд наблюдателя последовательно сканирует выбранный сектор при этом каждому лучу будет соответствовать вертикальная линия развертки на экране. В связи с этим, число отсекаемых лучей,как правило, выбирается равным горизонтальному расширению экрана.Объем вычислений по расчету точек пересечения значительно сокращается при использовании регулярного пространства.АОЛ за цикл своей работы автоматики выполняет следующие операции:

1) удаление невидимых поверхностей;

2) создание перспективы;

3) образование теней и освещения;

4) отображение текстуры объекта.

В общем случае АОЛ состоит из семи этапов:

1) предварительный;

2) вычисление координат первого пересечения с координатной

сеткой;

3) вычисление последних пересечений с координатной сеткой;

4) определение расстояний до точек пересечения;

5) масштабирование;

6) устранение проекционного искажения;

7) отображение линии развертки.

Этап 1

На предварительном этапе осуществляются следующие операции:

1) формирование табличных значений тригонометрических функций;

2) выделение в оперативной памяти рабочего пространства;

3) формирование начального заполнения кадра развертки;

Формирование табличных значений. Данная операция заключается в выделении памяти и заполнении таблицы тригонометрических функций, используемых при геометрических расчетах. Замена функциональных выражений на табличное значение является стандартным приемом, позволяющим ускорить обработку данных.

В данном случае для проведения геометрических построений требуется определить синус, косинус, тангенс при угле от 00 до 3600. Количество элементов таблиц легко определить по следующей формуле:

где L - ширина кадра, α - угол наблюдения.

Выделение рабочего пространства. Выделение рабочей памяти для объектного пространства происходит по заранее подготовленным исходным данным.

При формировании пространства образуется двойная система координат объекта:

1) координаты текущего куба;

2) координаты объекта внутри этого куба.

Начального заполнения кадра. Формирование фона в простей-

шем случае осуществляется делением экрана на две половины:

пол/потолок или земля/небо. В более сложных вариантах могут ис-

пользоваться текстуры для этих объектов.

Этап 2

Для вычисления координат первого пересечения используют уравнение прямой:

где α - угол наклона относительно горизонта, xн,yн – положение наблюдателя; xi, yi – искомая точка.Исходя из этой формулы, можно вычислить координаты точек

пересечений с сеткой моделируемого пространства:

Этап 3

Возможны два варианта пересечений луча-наблюдателя с координатной сеткой: с меридианами и параллелями.Пересечение с вертикальными гранями будем называть пересечением с Х-гранями, с горизонтальными – пересечение с Y-гранями.

Согласно вышеприведенным рисункам последовательные вычисления производятся через приращение координат:

Рис.8.2. X- и Y-грани

Здесь: m - размер сетки, k – наклон луча наблюдения относительно координатной сетки.

После определения очередной координаты x или y необходимо проверить наличие в этом кубе объекта. Если на пути следования луча такой объект есть, то переходим к этапу 4. В противном случае этап 3 повторяем.

 

 

Этап 4

Расстояние от наблюдателя до ближайшего объекта по направле-

нию следования луча определяется по одной из формул (рис.7.3):

 

Этап 5

Определив расстояние до точки пересечения, можно определить масштаб ее отображения в кадре:

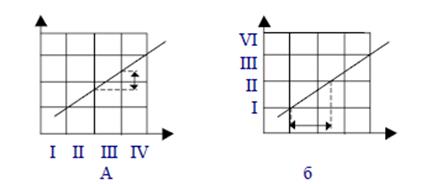
где k - коэффициент, подбирающийся эмпирически.

Этап 6

Необходимость устранения искажений объясняется тем, что при формировании кадра, содержащего объекты, находящиеся на малом расстоянии друг от друга, возникает эффект рыбьего глаза (рис.7.4).

Для устранения искажения масштаб S делят на cos β:

где β - отклонение луча от нормального изображения.

Этап 7

Если для отображения куба используются не текстурированные объекты (одного цвета), то вертикальная линия развертки определяется следующим образом

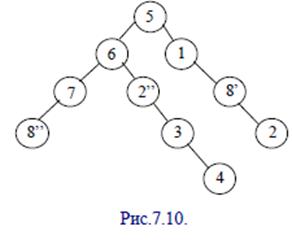
где L0- линия горизонта, S’ – величина, полученная на предыдущем

этапе.__

Конец 62 вопроса.
63.Алгоритм двоичного разбиения пространства (BSP-алгоритм).

Алгоритмы данной группы относятся к алгоритмам сортировки многоугольников. Принцип работы эти многоугольников заключается в следующем: если в объектном пространстве провести вертикальную плоскость, то она разделит все объектное пространство на 2 полупространства. Если продолжать разбиение полученных полупространств далее, располагая в каждом новом полупространстве по одному объек-

ту сцены, то в итоге получится разбиение пространства на кластеры, внутри которых находится по одному многоугольнику или грани. Отличительной особенностью этого разбиения является то, что элемент, расположенный в полупространстве, где нет наблюдателя, не могут перекрывать элементы полупространства, в котором находится наблюдатель. Это позволяет значительно сократить объем перебора взаимных перекрытий

объектов. На практике разбиение пространства продолжится до тех пор, пока в каждом

полупространстве (кластере) не останется одна грань. Последующее отображение граней, начиная с самого дальнего кластера, позволяет получить корректные проекции 3D-пространства.Алгоритмы просмотра полупространств (граней) можно представить в виде двоичного дерева, описывающего разбиение пространств. Это дерево называется

Binary Space Partitioning (BSP)Tree. Узлами BSP дерева являются плоскости, вдоль которыхпроизводится разбиение. Каждая плоскость описываетсяуравнением Ax+By+Cz=D или в нормальном вида p ⋅ n = D, где n - вектор нормали к поверхности.

Каждый узел BSP-дерева взвешивается следующей информацией, оформленной следующей структурой:

1) идентификатор грани, вдоль которой проходит плоскость разбиения;

2) координаты грани;

3) нормаль к поверхности грани;

4) указатель на вершину BSP-дерева, связанную с соседним положительным полупространством, то есть для которого p ⋅ n > D;

5) указатель на вершину из отрицательного полупространства p ⋅ n < D.

Обычно в качестве разбивающей плоскости выбирается плоскость, проходящая через одну из граней объектов сцены.Все грани, пересекаемые этой плоскостью, разбиваются на 2 части,которые помещаются в соответствующие ветви дерева (поддеревья).

Если разбивающая грань группы 5, то она делит грани 2 и 8 на две части. После этого деления образовалось 2 кластера (верхний и нижний). В верхнем выберем за плоскость разбиения грань 1, а в нижнем – грань 6.В нижнем кластере после деления по направлению 6-ой грани кластер делится на две части: левую и правую.

Движение продолжается далее,пока в кластер не будет входить по одной грани. BSP-дерево для этого случая выглядит таким образом, как представлено на

Особенность этого дерева в том, что получающиеся при двоичном делении деревья сильно зависят от выбора на каждом шаге разбивающей грани.

Для приведенного примера можно выбрать другую последовательность разбиений, которая описывается другим BSP-деревом (рис.7.11).

 

При этом не требуется разбиение граней.Итерационный процесс построения BSP-деревьев реализуется за три шага:

1) выбор разбивающей плоскости или грани;

2) разбиение множества всех граней на 2 части: положительная или отрицательная. При этом может возникать дробление грани;

3) рекурсивное обращение для каждой из получившихся после де-

ления частей.

Так как построение BSPдерева для одной и той же сцены не однозначно, то возникает вопрос выбора построения оптимального BSP-дерева.В качестве критерия оптимизации данного процесса можно выбрать один из двух следующих показателей.

1. Высота BSP-дерева.

Минимальная высота hmin гарантирует получение максимальной сбалансированности относительно левой и правой ветвей дерева. Это обеспечивает минимальное число проверок.

2. Количество разбиения граней S. Появление дополнительных граней, после их деления, увеличивает затраты по памяти и по времени на отображение сцены. Поэтому стремятся уменьшить этот показатель. Критерии hmin и Smin являются взаимно противоречивыми. Поэтому на практике выбирают компромиссный вариант – аддитивный критерий, включающий в себя оба взвешенных критерия. Получить полное оптимальное решение почти невозможно из-за большого числа граней в реальных 3D сценах. Поэтому при программной реализации алгоритмов, основанных на BSP-деревьях, используют эвристические приемы, позволяющие сократить объем вычислений. Например, на ка-

ждом шаге итерационного алгоритма рассматриваются не все кандидаты на разбиение, а какая то их часть. Количество рассматриваемых граней-кандидатов и принцип отбора влияет на достоверность используемой эвристики.

После построения BSP-дерева можно приступать к выполнению

процедуры рендеринга или визуализации. В алгоритмах данной группы используются 2 варианта алгоритма рендеринга:

1) BTF – алгоритм;

2) FTB – алгоритм.

BTF – алгоритмы позволяют получать окончательный результат наиболее естественным путем. В процессе рендеринга появляющиеся позже ближние объекты перекрывают удаленные. Недостаток этого метода: большая трудоемкость, связанная с лишними вычислениями на удаленные невидимые грани объектов. Алгоритм FTB позволяет устранить этот недостаток. Так как первыми на экран отображаются ближние к наблюдателю грани. Чтобы не выполнять лишних расчетов для невидимых дальних граней используется механизм отслеживания заполненных пикселей экрана. Для этого

могут использоваться маски или счетчики. Как только все пиксели заполнены, обход BSP-дерева прекращается.

Недостатком данного алгоритма являются дополнительные вычислит