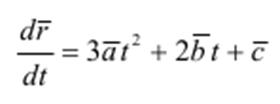Каркасные модели. Модели твердого тела.

Каркасные модели ориентированы на графические системы малой и средней производительности. В составе современных технических средств САПР и ИС каркасные модели используются для предварительного просмотра (preview) трехмерных объектов или сцен. Во многих практических приложениях каркасные модели используются на стадии проектирования.

Преимущества каркасных моделей:

• малый объем описания модели;

• простота алгоритмов построения каркасов;

• низкие требования к аппаратным и программным средствам.

Недостатки каркасных моделей:

• не сохраняет информацию о площади поверхности проектируемых объектов;

• не ориентированы на алгоритмы удаления невидимых линий и поверхностей;

• не позволяет строить контурные линии моделируемых объектов.

Область применения: предварительный просмотр в системах 3D- моделирования и анимации.

3.1.2. Геометрические модели твердого тела

Различают две группы геометрических моделей:

• модели конструктивной геометрии, или структурные, модели;

• поверхностные, или граничные, модели, среди которых различают кусочно-аналитические и алгебрологические модели.

Модель конструктивной геометрии описывается в виде бинарного дерева (графа) G = (U, V),

где U - множество вершин, соответствующих множеству используемых базовых элементов формы (БЭФ), V- множество операций между БЭФ, определяющих соединения и взаимное положение БЕФ между собой.

Каждый БЭФ идентифицируется своим именем, типом, а также следующим набором атрибутов: < x, y, z, α x, α y, α z, s x, s y, s z >, где x, y, z - координаты точки привязки локальной системы координат БЭФ к системе координат объектов, α x, α y, α z - углы поворота БЭФ относительно осей координат, s x, s y, s z - метрические параметры БЭФ (масштабы по осям координат).

Каждый базовый элемент формы может быть задан как в граничном, так и в каркасном представлении.

Достоинства данной модели:

1. Простота геометрических моделей базовых элементов формы

2. Простота алгоритмов БЭФ

3. Низкие требования к аппаратным и программным средствам

Недостатки:

1. Ограниченные возможности моделирования геометрических объектов.

2. Сложность восприятия результата моделирования сложных ГО или сцен, включающих множество ГО.

Область применения: предварительный просмотр в системах трехмерного моделирования и анимации.

Кусочно-аналитическая модель представляет собой простейший вариант граничных моделей. В ее основе лежит математическое описание элементов конструктивной геометрии. При помощи метода редукции добиваются сведения операций в трехмерном пространстве к опе- рациям на плоскости. Данная модель имеет иерархический вид, кото- рый занимает четыре уровня:

1) геометрический объект представляется в виде совокупности граней O i = <A ij>.

2) каждая грань представляется в виде цикла ребер A ij = < B ijk >.

3) каждое ребро описывается при помощи двух концевых точек B ijk =< b ijk1, b ijk2>.

4) каждая точка описывается тремя координатами b ijkl = <x ijkl, y ijkl, z ijkl >.

Алгебрологическая модель позволяет описывать более сложные конструкции объектов, при построении данной модели используется математический аппарат аналитической геометрии, теории множеств и булевой алгебры. В общем случае алгебрологическая модель представляет собой совокупность аналитических уравнений ориентированных поверхностей, дополненных множеством теоретико-множественных формул, определяющих взаимосвязи и взаиморасположение отдельных поверхностей: P i = f i(x, y, z).

Данные поверхности делят пространство на два подпространства, которые определяются следующими неравенствами: f i(x, y, z) ≥ 0; и f i (x, y, z) ≤ 0.

Внутри области твердотельного объекта определяется значением функции поверхности объекта f i ≥0, при помощи теоретикомножественных операций из поверхности f i можно образовать геометрические объекты F(f 1, f 2,…, f i,…, f n).

Достоинства моделей твердого тела.

1. Основным достоинством данной группы моделей является их простота и как следствие

2. Высокая скорость обработки данных моделей на компьютере.

Недостатки моделей твердого тела.

1. Не всегда можно подобрать базовый элемент формы либо аналитическое выражение f i для произвольной поверхности геометрического объекта.

2. При попытке сделать это поверхность становится очень сегментированной, что приводит к значительным вычислительным затратам на ее обработку.

3.1.3. Модели сложных скульптурных поверхностей

Все алгоритмы, относящиеся к данному виду моделирования можно разделить на две группы, связанные с обработкой двух видов моде- лей поверхности:

• полигональные модели;

• криволинейные модели.

Полигональные модели позволяют описывать сложные геометрические объекты при помощи множества плоских многоугольных, в общем случае, граней. Данные модели находят свое применение в программах, требующих быстрой динамичной смены изображения (системы виртуальной реальности, мультимедиа, игры). В большинстве случаев на практике грани представляются треугольниками.

Криволинейные модели позволяют наиболее реалистично изображать максимально сложные технические объекты и объекты природы. Для этих моделей поверхность сложного объекта разбивается на сегменты при помощи каркасно-мнемонического метода, любая поверхность при помощи какого-либо формального приема сокращается с максимально необходимой степенью точности. В любом случае скульптурная поверхность перед составлением ее модели должна быть "считана" при помощи трехмерных сканеров, либо создана средствами трехмерного моделирования.

При работе со скульптурными поверхностями используются три группы методов:

• методы аппроксимации (от лат. approximare – приближаться, методы приближенного описания), которые позволяют сохранить описание сложных кривых линий и поверхностей в виде простых уравнений;

• методы интерполяции (от лат. interpolatio – изменение – методы приближенного восстановления), которые позволяют по приближенно сохраненным данным восстановить исходную форму кривых линий и поверхностей;

• методы сглаживания, которые в обязательном порядке используются при работе с полигональными моделями и достаточно час- то - при построении качественных криволинейных поверхностей.

Конец 32 вопроса.
33. Параметрическое описание пространственных кривых. Модели кривых линий.

Перед тем, как приступить к описанию моделей криволинейных поверхностей, необходимо рассмотреть способы представления и описания пространственных кривых, используемых в качестве направляющих и образующих в процессе формирования сложной поверхности. Их геометрии известны два способа аналитического описания кривых линий:

• явное описание функциональной зависимости F(x, y, z);

• параметрическое описание - описание, в котором используются дополнительные параметры, через которые определяются аргументы функции x(t), y(t), z(t).

Широко используемое в начальных разделах геометрии явное описание кривых имеет следующие недостатки при решении практических задач автоматизации построения трехмерных кривых и поверхностей:

1. Производная функции может достигать значение бесконечности f′(x, y, z)→∞

2. Возникают сложность при проверке принадлежности точки кривой (например, для периодических зависимостей или для зависимостей, имеющих графики с петлями)

В случае использования параметрического описания данная проблема устраняется, т.к. параметрическая форма достаточно легко описывает замкнутые кривые, периодические и другие многозначные функции. Вместо значений производных в параметрическом описании фигурируют касательные векторы, которые всегда имеют конечную длину. Кривые линии и поверхности могут описываться параметрическими уравнениями произвольного порядка. Однако следует иметь в виду, что неправильно выбранный порядок уравнений приводит к ухудшению качества аппроксимации.

При значительных степенях параметрических уравнений также может наблюдаться ухудшение результата за счет возникновения изломов и разрывов. Поэтому на практике наибольшее распространение по- лучили параметрические уравнения третьей степени или параметрические кубические кривые:

Без потери общности можно считать, что значения параметра t лежит в диапазоне t ∈ [0;1]. Для определения гладкости кривых линий будем использовать значение производной:

В прикладной аналитической геометрии используется понятие C (i) -непрерывности, которая определяет функцию, непрерывную на исследуемом интервале и имеющую непрерывные первые i производных. Например, C (0) – непрерывность определяет функцию, не имеющую разрывов, C (1) - непрерывность определяет функцию, имеющую непрерывность касательных, а C (2) - непрерывность, определяет функцию, имеющую непрерывность вектора кривизны.

Конец 33 вопроса.