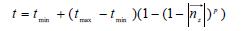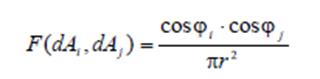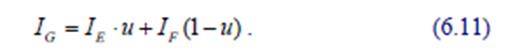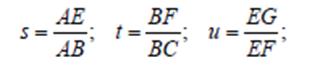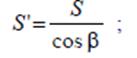Моделирование прозрачности и теней.

Для получения наиболее реалистичных изображений кроме отраженного света необходимо учитывать его преломление различными прозрачными и полупрозрачными объектами и средами. При этом необходимо учитывать соотношение, определяемое законом Снелиуса:

где η 1, η 2 – показатели преломления двух сред; ϕ – угол падения; ψ – угол

преломления.Падающий и преломленный лучи должны находится в одной плоскости. Ни

одно из прозрачных веществ или сред не пропускает свет полностью, т.е. при

наличие эффекта преломления обязательно будет происходить частичное отражение светового потока.

Преломление света бывает двух видов:

• направленное (зеркальное);

• диффузное.

Направленное преломление характерно для прозрачных веществ и сред. При этом искажения возникают только за счет криволинейной поверхности объекта или возмущений поверхности среды.

Диффузное преломление учитывает рассеивание световой энергии при прохождении света через вещество. При этом возникает эффект полупрозрачности или матового изображения. Формулы моделирования прозрачности объектов и сред являются составной частью алгоритмов отсечения невидимых поверхностей. В простейшем случае,

при обработке 3D прозрачная поверхность рассчитывается как линейная комбинация с находящейся за ней поверхностью:

I=I1t1+I2(1-t)

где I1, I2 – интенсивности отраженного света соответственно прозрач-

ной поверхности и поверхности, находящейся за ней; t – определяет

степень прозрачности и находится в интервале [0;1].

При t=0 моделируется максимальная прозрачность рассматриваемого объекта. А при t=1 объект, находящийся на первом плане полностью не прозрачен. Изменяя величину параметра t в ходе 3D -моделирования можно, для достижения максимальной демонстративности, добиваться удаления поверхности.Кроме того, это соотношение можно применять рекурсивно, моделируя таким образом ряд прозрачных объектов, находящихся один за другим.

Для моделирования объектов и поверхностей, имеющих сложные криволинейные формы, моделирование прозрачности при помощи линейной комбинации будет создавать не реалистичный эффект. Поэтому для таких объектов используется не линейная аппроксимация по следующей формуле:

где tmin, tmax – предельные значения прозрачности объектов; nz – проекция нормали к поверхности на ось OZ; P – коэффициент, определяющий кривизну поверхности.

В результате применения этого соотношения прозрачность пикселя t будет меняться в зависимости от расположения этого пикселя на поверхности.

В практике 3D- моделирования достаточно часто используются алгоритмы, работающие на основе Z-буфера (буфер глубины). Но в этой группе алгоритмов напрямую не возможно использовать много-световые эффекты, в том числе эффект моделирования прозрачности.

Это объясняется тем, что данные алгоритмы сохраняют z координаты только для ближайших к наблюдателю объектов.

Чтобы устранить этот недостаток, в алгоритмах с Z-буфером формируется специальный буфер прозрачности. Кроме того, в более сложные алгоритмы могут дополняться дополнительными буферами интенсивности и коэффициентов преломления.

. Моделирование теней

Тени на объектах сцены наблюдаются в том случае, если положение источника света и наблюдателя не совпадают. Тень состоит из двух частей:

• полной тени;

• полутени.

Полная тень – это темная, резко ограниченная область, которая создается точечным источником света. Полутень – это тень, которая создается распределенным источником света, имеющим конечный размер. Она охватывает полную тень по периметру, образуя размытые края. Объем вычислений при расчете теней, кроме всего прочего, зависит от расположения источников света. Возможны три варианта расположения:

1) источник света расположен в бесконечности, при этом направление лучей света, по которым просчитываются тени, соответствует

ортогональному проецированию, т.е. простейшему виду проецирования, а это определяет минимальные затраты на вычисление теней в данном случае;

2) источник света находится на конечном расстоянии вне поля зрения наблюдателя (камеры); в этом случае отслеживание лучей совпадает с перспективным проецированием, что увеличивает вычислительные затраты;

3) источник света находится на конечном расстоянии и попадает в поле зрения наблюдателя; этот случай аналогичен предыдущему, но требует дополнительных затрат на деление сцены по секторам и индивидуальный просчет.

При построении теней выполняется операция, реализующаяся за два шага:

1) построение тени в 3D-виде или относительно источника;

2) построение тени в двумерном виде или относительно наблюдателя.

При этом можно выделить собственные тени объектов и тени

проекционные, образуемые на поверхности объекта другими объектами сцены.

Алгоритм построения собственных теней аналогичен удалению

невидимых поверхностей. А алгоритм построения проекционных теней сводится к построению проекции всех не лицевых граней объектов на сцену. Центр проекции – источник света. При перемещении наблюдателя не надо выполнять пересчет теней, т.к. их положение в 3D сцене зависит от положения источника света.

Конец 56 вопроса.
57.Методы трассировки лучей. Алгоритмы прямого хода луча.

Методы прямого хода лучей

Методы этой группы можно разделить на три группы:

1) алгоритмы Back-To Font (BTF)

2) алгоритмы Font-To back (FTB)

3) алгоритмы сплаттинга (Splatting).

Алгоритмы, относящиеся к группе BTF, похожи на алгоритмы использующие Z- буфер. Отличаются только тем, что перед выполнением самой процедуры рендеринга осуществляется сортировка объектов сцены в порядке уменьшения расстояния до наблюдателя. После выполнения этой сортировки необходимость в Z- буфере отпадает.

Алгоритмы, относящиеся к группе FTB, аналогичны методам группы BTF с той лишь разницей, что предварительная сортировка осуществляется в порядке удаления от наблюдателя.

Алгоритмы сплаттинга (splatting) ориентированы на построение наиболее реалистичных изображений. Это происходит за счет того, что при отображении каждого трассируемого луча в воксель (voxel – от англ. volume element - элемент трехмерного пространства) происходит размытие этого луча по соседним пикселям. Для реализации более реалистичного размытия строятся таблицы размытия следа луча, хра-

нящие отпечатки вокселей. Эти отпечатки при окончательном рендеринге смешиваются с

массивом изображения.

Достоинствами методов прямого хода лучей является:

1) максимально возможная для трассировки лучей реалистичность;

2) возможность просчета сцены, содержащей прозрачные и полупрозрачные материалы.

Недостатки методов прямого хода лучей:

1) плохо работает с диффузными поверхностями;

2) необходимость полного пересчета сцены при изменении положения наблюдателя;

3) значительный объем вычислений может уходить на просчет невидимой части сцены.

Конец 57 вопроса.
58.Методы трассировки лучей. Алгоритмы обратного хода луча.

Алгоритмы этой группы выполняют просчет, только тех лучей,которые в конечном итоге доходят от источника света до наблюдателя. Благодаря этому приему удается значительно сократить объем вычислений. Поэтому алгоритмы этой группы являются базовыми для большинства систем трехмерного моделирования.Общая схема алгоритма обратной трассировки заключается в следующем: просчет луча начинается от точки наблюдения. Лучи проводятся через пиксели экрана до пересечения с ближайшим объектом

(вокселем). Освещенность этой точки складывается как из отраженных или переломленных лучей, так и лучей исходящих непосредственно от источников света. Во втором случае эта точка напрямую соединяется с каждым из источников света, присутствующих в сцене.

В алгоритмах данной группы рассматриваются только те источники, которые видны из рассматриваемой точки. Для вычисления остальных составляющих освещения данной точки строятся вторичные лучи, направляемые на отражающие и преломляющие объекты. При моделировании диффузных поверхностей, в точке пересечения луча с

такой поверхностью порождается пучок лучей, равномерно распределенный по всем направлениям.На основании простейшей модели точечного источника света и

идеальной поверхности можно получить дерево прохождения каждого луча по сцене. Вершины такого дерева будут соответствовать точкам пересечения луча с поверхностями объектов, а дуги – направлению луча в пространстве. Даже в простейшем случае луч может отражаться и преломляться. Таким образом, для реальных сцен один луч может

породить дерево, насчитывающее десятки, сотни, тысячи вершин. Для уменьшения объема вычислений вводят ограничения на глубину дерева. Так как по мере прохождения луча по сцене его энергия рассеивается, то можно ввести значение пороговой интенсивности, по достижении которой трассировка любой ветви дерева прекращается.

Для получения полноцветного изображения, указанную схему просчета лучей необходимо провести для каждого из трех компонент света (R, G, B).

Достоинства методов обратного хода лучей:

Снижение трудоемкости вычислений по сравнению с прямой трассировкой, что позволяет (в отдельных случаях) выполнить рендеринг не только отдельных кадров, но и видео ряда в реальном масштабе времени.

Недостатки методов обратного хода лучей:

1) плохая работа с диффузными поверхностями;

2) зависимость от положения наблюдателя;

3) неполный учет освещенности сцены.

 

Конец 58 вопроса.
59.Построения реалистических изображений методом излучательности.

Этот метод (Radioсity) был призван устранить два основных недостатка метода трассировки лучей:

1) зависимость от положения наблюдателя;

2) большой объем вычислений при обработке диффузных поверхностей.

Алгоритмы данной группы базируются не на вычислении интенсивности, а на расчете энергетического поля. Основой для построения этой модели является закон сохранения энергии в замкнутой системе. Все объекты, присутствующие в сцене, делятся на фрагменты, для которых составляются уравнения баланса энергии:

где Bi – энергия отражаемая i -им фрагментом; Ei - энергия, выделяемая объектом; Ki – коэффициент отражения i- ого фрагмента; Fij – коэффициент формы, определяющий долю энергии j- ого объекта, попадающую на рассматриваемый i -й фрагмент; Bj – энергия, отражаемая любым другим фрагментом сцены. Вся сцена, таким образом, может быть описана при помощи системы линейных уравнений. Эта система уравнений обладает диагональным преобладанием, так как получается псевдодиагональная матрица.

Для решения подобной системы уравнений применяются широко

известные итерационные методы, которые за незначительное число шагов дают приемлемую точность решения. Уравнение энергетического баланса составляются для каждой компоненты света R, G, B.

Легко заметить, что математическая модель метода излучательности зависит от геометрии сцены и не зависит от положения наблюдателя. Кроме того, просчет различных форм отражения или преломления с вычислительной точки зрения эквивалентен.

 

Геометрия сцены описывается при помощи коэффициентов формы – Fij. Вычисление данных коэффициентов представляет собой достаточно сложную процедуру, занимающую большую часть времени вычислений по методу излучательности.

Коэффициенты формы Fij рассчитываются следующим образом.

Рассмотрим два фрагмента сцены - Аi Аj (рис.6.15). Для каждого из фрагментов выберем элементарный фрагмент dAi и dAj. Fij для элементарного фрагмента рассчитывается следующим образом:

Для получения полного коэффициента формы необходимо проинтегрировать формулу (6.22) по поверхности Ai и Aj. (6.23)

В данной формуле не учитывается возможные изменения углов ϕ i, ϕ j и расстояний r. Этими отклонениями можно пренебречь, если выбирать элементарные фрагменты dAi и dAj в центре основного фрагмента. Кроме того, эта формула не учитывает возможности перекрытия объектов. Для учета этого обстоятельства в формулу (6.23) вводится

функция Hij, которая определяет видимость j -ого объекта со стороны i ого и наоборот:

 

Конец 59 вопроса.
60.Модель закраски Гуро.

Метод Гуро (Gouraud shading) был разработан в 1971 году. Данный метод предназначен для сглаживания полигональной поверхности на базе линейной интерполяции интенсивности света. Рассмотрим работу метода на следующем примере.

Пусть существует грань ABCD, принадлежащая полигональной поверхности. Рассмотрим одну из строк растра, пересекающую в процессе сканирования данную грань.

Задача заключается в определении интенсивности света в каждой точке на

поверхности грани. Исходными данными для расчета являются интенсивности в угловых

точках A, B, C, D, которые рассчитывается по одному из вариантов формулы

закраски. При этом следует помнить, что для полигональной поверхности

лучше брать формулы, не учитывающие зеркальную составляющую.Расчет произвольной точки G, находящейся внутри грани полигональной поверхности, базируется на значениях интенсивностей точек пересечения текущей строки растра с гранями (точки E и F на рис. 6.7). Вычисление этих точек, в свою очередь, базируются на расчетах, полу-

ченных для вершин граней АВ и ВС. Интенсивность света в точке Е ребра АВ на основе линейной интерполяции может быть представлена следующим образом:

s – параметр (s ∈ [0, 1]), определяющий положение точки на ребре АВ.

Аналогичным образом вычисляется интенсивность точки F:

Аналогичным образом определяется и интенсивность точки, расположенной на отрезке ЕF:

При этом значение параметров определяется следующим образом:

 

Используя формулы (6.9) - (6.11) можно определить интенсивность света, в каждой точке в пределах грани ABCD.

Процесс вычисления интенсивности в произвольной грани, можно значительно ускорить, если определить рекурсивную зависимость между значениями интенсивностей двух соседних пикселей, расположенных на строке развертки, пересекающих грань:

где Δ I - перепад интенсивности между крайними точками, рассматриваемой строки развертки; Δ U - расстояние между соседними точками строки развертки, выраженное в величинах параметра, привязанного к рассматриваемому отрезку.

На основании формул (6.9) – (6.12) можно построить алгоритм, выполняющий закраску по методу Гуро, который будет состоять из следующих четырех шагов:

1) проецирование вершин граней полигональной поверхности на плоскость экрана.

2) вычисление интенсивностей света в этих точках, на основании формул закраски (без учета зеркальной составляющей).

3) определение координат концов отрезка для граней, пересекаемых строкой развертки и вычисление интенсивности в них.

4) вычисление интенсивности пикселей, расположенных на отрезке, соответствующей строке растра по формуле (6.12).

Достоинства метода Гуро:

- простота алгоритма;

- гарантия непрерывного изменения интенсивности в пределах

одной грани и при переходе между соседними гранями;

- высокое быстродействие за счет наличия рекуррентного соотношения для интенсивности в пределах одной грани.

Недостаток метода Гуро:

метод не обеспечивает гладкости изменения интенсивности,

следствием чего являются:

1) усреднение интенсивности в середине грани, что приводит к отображению плоских поверхностей;

2) возможно появление полос Маха1, которые представляют эффект увеличения интенсивности на границах областей с постоянной яркостью.

Для устранения недостатков данного метода был предложен метод, базирующийся на интерполяции векторов-нормалей к поверхностям граней.

1 Полосы Маха – эффект увеличения интенсивности у границ областей

Конец 60 вопроса.

Модель закраски Фонга.

Данный метод превосходит метод Гуро по объемам вычислений, однако позволяет добиться более высокого качества сглаживания полигональных поверхностей.

Метод Фонга (Phong Shading) также базируется на линейной интерполяции. Однако в качестве интерполируемой величины выступает не интенсивности точек поверхности, а векторы нормалей к поверхности в этих точках.

Метод Фонга заключается в построении для каждой точки поверхности вектора-нормали G U. На базе полученного значения G U производится вычисление интенсивности 0 I. Схема интерполяции аналогична схеме, приведенной для метода Гуро. При этом нормали в вершинах полигональной сетки определяется как сумма нормалей прилегающих гра-

ней:

где i k - коэффициент, определяющий вес грани среди всех граней, которые имеют общую вершину.

Для вычисления нормали G U, используются значения векторов

Для расчета значений интенсивности, используются формулы закраски, в которых вместо углов α и β используются векторы-нормали по соответствующим направлениям. Благодаря этому, метод Фонга поzволяет получить более реалистичный эффект сглаживания, позволяющий учитывать зеркальную составляющую отраженного света.

Достоинства метода Фонга:

- гарантированная гладкость изменения интенсивности;

- в большинстве случаев устраняет эффект Маха, присущий методу Гуро;

- обеспечивает высокое быстродействие за счет наличия рекурсии в вычислениях.

Недостатки метода Фонга:

- возможны ошибки при вычислении большого числа невыпуклых многоугольников;

- не исключена возможность появления полос Маха (например,для сфер эффект Маха усиливается).

Конец 61 вопроса.

 

 

Алгоритм отсечения лучей.

Алгоритм отсечения лучей (Ray Casting) является простейшим вариантом алгоритмов обеспечивающих виртуальную реальность. Наиболее известно использование этого алгоритма в качестве графического ядра первых 3D игровых программ.

 

 

Алгоритм отсечения лучей(АОЛ) можно рассматривать как упрощенный вариант алгоритма трассировки лучей с обратным ходом луча. Для упрощения реализации вычислительных функций данный алгоритм рассматривает простейшую геометрическую модель пространства в виде конечного числа кубов.Идея АОЛ заключается в том, что при построении каждого очередного кадра по направлению взгляда наблюдателя в этом пространстве отсекается сектор лучей (600-900). Все остальные лучи, выходящие за поле

просмотра, не рассматриваются, то есть отсекаются. В алгоритме не учитываются источники света и отражательные характеристики поверхности объекта. Учет освещенности производится статически, то есть описывается на старших формированиях пространства, и в момент выполнения алгоритма находится в описании кубов, из которых

сформировано объектное пространство.Динамические объекты сцены (движущиеся персонажи) реализованы в виде спрайтов1. Поэтому данное графическое ядро

относят к 2,5D графическим программам. После выделения сектора просмотра вычисляются координаты точек пересечения лучей с объектами пространства. Причем

лучи проводятся через каждый пиксель экрана.

1 Под спрайтом понимают семейство растровых изображений, отображающих фазы движения какого-либо объекта. Спрайт используется для формирования анимационных последовательностей в игровых и мультимедийных программах

Взгляд наблюдателя последовательно сканирует выбранный сектор при этом каждому лучу будет соответствовать вертикальная линия развертки на экране. В связи с этим, число отсекаемых лучей,как правило, выбирается равным горизонтальному расширению экрана.Объем вычислений по расчету точек пересечения значительно сокращается при использовании регулярного пространства.АОЛ за цикл своей работы автоматики выполняет следующие операции:

1) удаление невидимых поверхностей;

2) создание перспективы;

3) образование теней и освещения;

4) отображение текстуры объекта.

В общем случае АОЛ состоит из семи этапов:

1) предварительный;

2) вычисление координат первого пересечения с координатной

сеткой;

3) вычисление последних пересечений с координатной сеткой;

4) определение расстояний до точек пересечения;

5) масштабирование;

6) устранение проекционного искажения;

7) отображение линии развертки.

Этап 1

На предварительном этапе осуществляются следующие операции:

1) формирование табличных значений тригонометрических функций;

2) выделение в оперативной памяти рабочего пространства;

3) формирование начального заполнения кадра развертки;

Формирование табличных значений. Данная операция заключается в выделении памяти и заполнении таблицы тригонометрических функций, используемых при геометрических расчетах. Замена функциональных выражений на табличное значение является стандартным приемом, позволяющим ускорить обработку данных.

В данном случае для проведения геометрических построений требуется определить синус, косинус, тангенс при угле от 00 до 3600. Количество элементов таблиц легко определить по следующей формуле:

где L - ширина кадра, α - угол наблюдения.

Выделение рабочего пространства. Выделение рабочей памяти для объектного пространства происходит по заранее подготовленным исходным данным.

При формировании пространства образуется двойная система координат объекта:

1) координаты текущего куба;

2) координаты объекта внутри этого куба.

Начального заполнения кадра. Формирование фона в простей-

шем случае осуществляется делением экрана на две половины:

пол/потолок или земля/небо. В более сложных вариантах могут ис-

пользоваться текстуры для этих объектов.

Этап 2

Для вычисления координат первого пересечения используют уравнение прямой:

где α - угол наклона относительно горизонта, xн,yн – положение наблюдателя; xi, yi – искомая точка.Исходя из этой формулы, можно вычислить координаты точек

пересечений с сеткой моделируемого пространства:

Этап 3

Возможны два варианта пересечений луча-наблюдателя с координатной сеткой: с меридианами и параллелями.Пересечение с вертикальными гранями будем называть пересечением с Х-гранями, с горизонтальными – пересечение с Y-гранями.

Согласно вышеприведенным рисункам последовательные вычисления производятся через приращение координат:

Рис.8.2. X- и Y-грани

Здесь: m - размер сетки, k – наклон луча наблюдения относительно координатной сетки.

После определения очередной координаты x или y необходимо проверить наличие в этом кубе объекта. Если на пути следования луча такой объект есть, то переходим к этапу 4. В противном случае этап 3 повторяем.

 

 

Этап 4

Расстояние от наблюдателя до ближайшего объекта по направле-

нию следования луча определяется по одной из формул (рис.7.3):

 

Этап 5

Определив расстояние до точки пересечения, можно определить масштаб ее отображения в кадре:

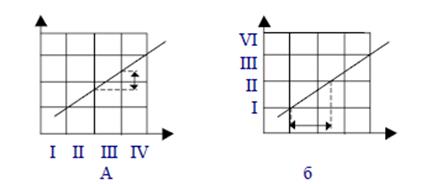
где k - коэффициент, подбирающийся эмпирически.

Этап 6

Необходимость устранения искажений объясняется тем, что при формировании кадра, содержащего объекты, находящиеся на малом расстоянии друг от друга, возникает эффект рыбьего глаза (рис.7.4).

Для устранения искажения масштаб S делят на cos β:

где β - отклонение луча от нормального изображения.

Этап 7

Если для отображения куба используются не текстурированные объекты (одного цвета), то вертикальная линия развертки определяется следующим образом

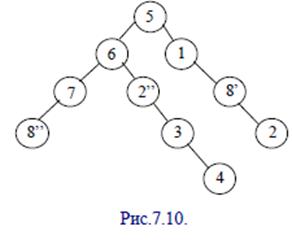
где L0- линия горизонта, S’ – величина, полученная на предыдущем

этапе.__

Конец 62 вопроса.
63.Алгоритм двоичного разбиения пространства (BSP-алгоритм).

Алгоритмы данной группы относятся к алгоритмам сортировки многоугольников. Принцип работы эти многоугольников заключается в следующем: если в объектном пространстве провести вертикальную плоскость, то она разделит все объектное пространство на 2 полупространства. Если продолжать разбиение полученных полупространств далее, располагая в каждом новом полупространстве по одному объек-

ту сцены, то в итоге получится разбиение пространства на кластеры, внутри которых находится по одному многоугольнику или грани. Отличительной особенностью этого разбиения является то, что элемент, расположенный в полупространстве, где нет наблюдателя, не могут перекрывать элементы полупространства, в котором находится наблюдатель. Это позволяет значительно сократить объем перебора взаимных перекрытий

объектов. На практике разбиение пространства продолжится до тех пор, пока в каждом

полупространстве (кластере) не останется одна грань. Последующее отображение граней, начиная с самого дальнего кластера, позволяет получить корректные проекции 3D-пространства.Алгоритмы просмотра полупространств (граней) можно представить в виде двоичного дерева, описывающего разбиение пространств. Это дерево называется

Binary Space Partitioning (BSP)Tree. Узлами BSP дерева являются плоскости, вдоль которыхпроизводится разбиение. Каждая плоскость описываетсяуравнением Ax+By+Cz=D или в нормальном вида p ⋅ n = D, где n - вектор нормали к поверхности.

Каждый узел BSP-дерева взвешивается следующей информацией, оформленной следующей структурой:

1) идентификатор грани, вдоль которой проходит плоскость разбиения;

2) координаты грани;

3) нормаль к поверхности грани;

4) указатель на вершину BSP-дерева, связанную с соседним положительным полупространством, то есть для которого p ⋅ n > D;

5) указатель на вершину из отрицательного полупространства p ⋅ n < D.

Обычно в качестве разбивающей плоскости выбирается плоскость, проходящая через одну из граней объектов сцены.Все грани, пересекаемые этой плоскостью, разбиваются на 2 части,которые помещаются в соответствующие ветви дерева (поддеревья).

Если разбивающая грань группы 5, то она делит грани 2 и 8 на две части. После этого деления образовалось 2 кластера (верхний и нижний). В верхнем выберем за плоскость разбиения грань 1, а в нижнем – грань 6.В нижнем кластере после деления по направлению 6-ой грани кластер делится на две части: левую и правую.

Движение продолжается далее,пока в кластер не будет входить по одной грани. BSP-дерево для этого случая выглядит таким образом, как представлено на

Особенность этого дерева в том, что получающиеся при двоичном делении деревья сильно зависят от выбора на каждом шаге разбивающей грани.

Для приведенного примера можно выбрать другую последовательность разбиений, которая описывается другим BSP-деревом (рис.7.11).

 

При этом не требуется разбиение граней.Итерационный процесс построения BSP-деревьев реализуется за три шага:

1) выбор разбивающей плоскости или грани;

2) разбиение множества всех граней на 2 части: положительная или отрицательная. При этом может возникать дробление грани;

3) рекурсивное обращение для каждой из получившихся после де-

ления частей.

Так как построение BSPдерева для одной и той же сцены не однозначно, то возникает вопрос выбора построения оптимального BSP-дерева.В качестве критерия оптимизации данного процесса можно выбрать один из двух следующих показателей.

1. Высота BSP-дерева.

Минимальная высота hmin гарантирует получение максимальной сбалансированности относительно левой и правой ветвей дерева. Это обеспечивает минимальное число проверок.

2. Количество разбиения граней S. Появление дополнительных граней, после их деления, увеличивает затраты по памяти и по времени на отображение сцены. Поэтому стремятся уменьшить этот показатель. Критерии hmin и Smin являются взаимно противоречивыми. Поэтому на практике выбирают компромиссный вариант – аддитивный критерий, включающий в себя оба взвешенных критерия. Получить полное оптимальное решение почти невозможно из-за большого числа граней в реальных 3D сценах. Поэтому при программной реализации алгоритмов, основанных на BSP-деревьях, используют эвристические приемы, позволяющие сократить объем вычислений. Например, на ка-

ждом шаге итерационного алгоритма рассматриваются не все кандидаты на разбиение, а какая то их часть. Количество рассматриваемых граней-кандидатов и принцип отбора влияет на достоверность используемой эвристики.

После построения BSP-дерева можно приступать к выполнению

процедуры рендеринга или визуализации. В алгоритмах данной группы используются 2 варианта алгоритма рендеринга:

1) BTF – алгоритм;

2) FTB – алгоритм.

BTF – алгоритмы позволяют получать окончательный результат наиболее естественным путем. В процессе рендеринга появляющиеся позже ближние объекты перекрывают удаленные. Недостаток этого метода: большая трудоемкость, связанная с лишними вычислениями на удаленные невидимые грани объектов. Алгоритм FTB позволяет устранить этот недостаток. Так как первыми на экран отображаются ближние к наблюдателю грани. Чтобы не выполнять лишних расчетов для невидимых дальних граней используется механизм отслеживания заполненных пикселей экрана. Для этого

могут использоваться маски или счетчики. Как только все пиксели заполнены, обход BSP-дерева прекращается.

Недостатком данного алгоритма являются дополнительные вычислительные затраты на поддержку механизма отслеживания заполненных пикселей.

Достоинства алгоритмов, базирующихся на построении BSP-

деревьев:

1) возможность визуализации нерегулярных пространств;

2) независимость BSP-дерева от расчетов проецирования, что

удобно для построения видеоряда (в пределах одного сегмента).

Недостатки:

1) необходимость разбиения грани, что ведет к увеличению

вычислительной сложности, особенно при обработке больших сцен;

2) не локальность BSP-деревьев: незначительное изменение сцены

может привести к изменению всего BSP-дерева;

3) невозможность добиться реалистичного освещения;

4) использование для движущихся объектов технологии спрайтов.

 

Конец 63 вопроса.