Классификация методов сжатия графической информации.

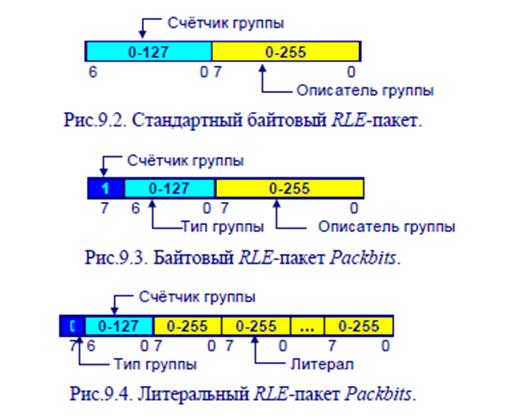
Графическая информация, как и большинство видов информации, несёт в себе избыточность. Поскольку объемы современной графической информации имеют значительные размеры, то при ее сохранении, эту избыточность желательно устранить. Для устранения избыточности существуют специальные методы, которые делятся на две группы:

• методы упаковки;

• методы сжатия.

Методы упаковки не устраняют информацию избыточности, а устраняют из потока пустые фрагменты (не несущие полезной информации).

Методы сжатия ориентированы на сведение информации избыточности к минимуму. Эти методы делятся на:

- методы сжатия с потерями;

- методы сжатия без потерь.

К методам упаковки и сжатия без потерь относятся следующие группы алгоритмов:

1) упаковка пикселей;

2) групповое кодирование;

3) методы, базирующиеся на словаре;

4) методы, базирующиеся на кодировании строк бит переменной длины.

К методам сжатия с потерями относятся:

1) JPEG-сжатие;

2) волновое сжатие (вейвлет-сжатие);

3) фрактальное сжатие.

Конец 67 вопроса.
68.Метод группового кодирования (RLE-алгоритм).

Алгоритмы данного семейства выделяют в потоке данных (в изображении) группы однородных элементов (байтов, пикселей) и выполняет замену этих групп парой чисел, одно из которых определяет значения повторяющихся элементов (цветовые характеристики байтов, пикселей), а другое – количество элементов в этой группе. В том случае, если в изображении в достаточном количестве присутствуют группы однородных элементов, происходит существенное сокращение объёмов информации. К сожаленью, в компьютерной графике подобные алгоритмы эффективно работают при малой цветности изображений - до 256 цветов (т.е. до 8 бит/пиксель).Эти алгоритмы в англоязычной литературе называются RLE алгоритмами (Run Length Encoding). RLE -алгоритмы классифицируются:

- по выделению кодируемых строк;

- по выделению кодируемых элементов.

По выделению кодируемых строк RLE -алгоритмы делятся на четыре группы:

а) ориентированные на горизонтальные строки;

б) ориентированные на вертикальные строки;

в) ориентированные на блочную упаковку;

г) ориентированные на змеевидные строки.

При этом варианты а и б просты для реализации. Однако имеют существенный недостаток - не учитывается двумерный характер графической информации. В вариантах в и г недостаток устранен.

Входные данные рассматриваются RLE -алгоритмом как одномерный поток. При этом в большинстве алгоритмов последовательность пикселей потока данных соответствует последовательности обхода экрану лучом сканирования: слева направо и сверху вниз. Однако существуют такие вариант RLE -алгоритмов, которые позволяют формировать последовательность пикселей в ином порядке (например, обход столбцов пикселей сверху вниз или зигзагом - от верхнего левого угла к правому нижнему). Подобные варианты RLE позволяют в отдельных случаях повышать степень сжатия данных, но на практике

применяются довольно редко.

По выделению кодируемых элементов RLE -алгоритмы делятся на:

а) бит–ориентированные;

б) байт–ориентированные;

в) пиксельно–ориентированные.

Вариант «а» целесообразно использовать только для монохром-

ных изображений. Вариант «б» наиболее универсален, т.к. он не зависит ни от формата машинного слова, ни от формата пикселя. Вариант«в» использует в качестве элементов потока двух, трех и четырех байтные пиксели.

Бит-ориентированные RLE -алгоритмы. RLE -алгоритмы данного вида выделяют группы одинаковых битов, игнорируя при этом границы байтов и слов. Этот вид алгоритмов эффективен только при обработке монохромных, или чёрно-белых, изображений (1 бит/пиксель). RLE -алгоритм битового уровня объединяет в группы от 1 до 128 битов,

создавая из них однобайтовые пакеты. Семь младших битов этого байта содержат счётчик группы (количество битов минус единица), а самый старший бит – описатель группы (рис.9.1). Группы длиной более 128 пикселей необходимо делить на несколько RLE -пакетов.

Байт-ориентированные RLE -алгоритмы. RLE -алгоритмы байтового уровня являются наиболее распространенными и объединяют в RLE -группы одинаковые байты. При этом каждая RLE -группа заменяется двухбайтовым RLE -пакетом. Первый байт содержит счётчик группы (от 0 до 255), а второй – описатель (рис.9.2). Кроме того, часто

применяется схема двухбайтового кодирования, позволяющая хранить в потоке закодированных данных литералы - группы неповторяющихся байтов (такой подход применен в одном из самых распространенных вариантов RLE -алгоритма - Packbits). При этом семь младших битов первого байта содержат счётчик группы (количество байтов в группе минус единица), а самый старший бит первого байта указывает тип

группы (RLE -группа или литерал). Если самый старший бит установлен в «1», то он определяет RLE -группу. RLE -группа восстанавливается по байту-описателю, повторяя его столько раз, сколько определяет счётчик группы (рис.9.3). Если же самый старший бит установлен в 0, то он определяет литерал. При этом следующие байты (в количестве, указанном счётчиком группы плюс единица) должны читаться напрямую из закодированных данных изображения. В этом случае байт счётчика группы содержит значения в диапазоне от 0 до 127 (количество байтов в группе минус единица). Смотрите рисунок. RLE -схемы байтового уровня эффективны для данных изображения, которые хранятся в виде одного байта на пиксель.

Пиксельные RLE -алгоритмы. RLE -алгоритмы пиксельного уровня используют в качестве элемента входного потока пиксели размером два, три или четыре байта. Сведения о размере пикселей хранятся, как правило, в заголовке растрового файла. На рис.9.5 приведен пример с трехбайтовым пикселем.

Кроме того, варианты RLE- алгоритмов могут отличаться для различных форматов

Конец 68 вопроса.
69.Методы кодирования строк бит переменной длины. Алгоритм Хаффмена и арифметическое кодирование.

Кодирование Хаффмена

Данный алгоритм принадлежит к группе алгоритмов кодирования битовых строк с переменной длиной. Исходный вариант алгоритма был предложен Дэвидом Хаффменом1 (David Huffman) в 1952 г. В основе лежит вероятностная оценка появления байтов (символов) во входном потоке кодированных знаков. При этом наиболее часто встречающемуся символу сопоставляется наиболее короткие коды, а редко встречаю-

щимся – наиболее длинные. Алгоритм используется при сжатии информации, передаваемой по каналам связи, а так же используется при кодировании графических

данных формата TIFF, JPEG. Рассмотрим работу алгоритма на примере. Пусть алфавит входного потока состоит из 6-ти символов: A, B, C, D, E, __ (пробел). Вероят-

ность появления этих символов приведена в табл.9.2.

Пусть входной поток содержит 1000 символов, что составляет в стандартном варианте (ASCII -код) 8000 бит (по байту на символ).Работа алгоритма начинается с построения бинарного дерева Хаффмена. Листья дерева – это символы, узлы – суммарные вероятности событий.

При построении дерева вверху располагается часто встречающиеся, внизу – редко встречаемые символы (рис.9.1).Произведем разметку дерева. Пусть каждая из левых дуг, выходящая из любой вершины дерева, соответствует коду «0», а правая коду «1» (рис.9.2).

В результате построения дерева Хаффмена символы будут иметь коды, представленные в табл.9.3.

Определим объем кода исходного потока символов.Зная вероятность появления каждого из символов, можем оценить длину суммарного выходного потока данных.

1000 ×(0,3×2 + 0,2×2 + 0,13 + 0,1×4 + 0,05×4 + 0,25×2) = 2400 (бит)

Показатель сжатия составит величину:

(1 – 2400/8000) × 100%=20%

Рассмотрим пример декодирования, используя предыдущее бинарное дерево Хаффмена (рис.9.2).

Пусть задана строка бит:

Очевидно, что для декодирования потока необходимо сохранять

полученное при кодировке дерево Хаффмена, либо знать вероятность

появления символа во входном потоке, что позволит восстановить дерево кодирования.

Декодирование осуществляется путём «пропускания» потока битов по бинарному дереву Хаффмена, при помощи которого осуществлялось кодирование информации. Передвижение по дереву происходит от корня до одного из листьев. После этого происходит возврат к корню дерева. Рассматриваемый поток бит приведет к следующему результату:

10 0000 001 0001 01 0001 11 10

А С В D __ D Е А

Алгоритм Хаффмана принят в качестве стандарта международным

консультативным комитетом по телеграфии и телефонии (CCITT2). Для

кодирования в телекоммуникационных сетях существуют два варианта

стандарта: CCITT T.4 (или Group3), CCITT T.6 (или Group4). Существует

третий вариант - IBM MMR – фирменная реализация алгоритма Хаффмена IBM.

CCITT T.4 (Group3). Предназначен для кодирования текстовой

информации и черно-белых изображений в телекоммуникациях. Во всех

факс-машинах данный вариант реализован на аппаратном уровне. Поддерживается коррекция ошибок. При кодировании графической информации возможны два варианта: G31D, G32D.

Алгоритмы данной группы позволяют сжимать текст в 5-8 раз, изображения – в 2-3 раза.

G31D. Перед реализацией алгоритма осуществляется статисти-

ческий анализ групп. Длина группы описывается двумя типами кодо-

вых слов:

- образующие (для длинных слов);

- терминальные (для коротких слов).

Закодированная группа пикселей состоит из терминальных кодо-

вых слов и образующих кодовых слов. Кроме того, во входной поток

добавляются управляющие символы конца строки EOL (12 бит) и сим-

волы синхронизации RTC, которые используются для контроля.

G32D. Алгоритм ориентирован на описание плоских изображений. В нём описываются базовые строки (полностью) и строки разницы, содержащие только отличия между строками. Для показания сжатия используется k-фактор, указывающий количество строк, через которое осуществляется полное кодирование (бывает либо k=2, либо

k=4).

CCITT T.6 (Group4). Алгоритм ориентирован на более современные и надежные вычислительные сети и поэтому не использует поддержку коррекции ошибок. Алгоритм позволяет достигать 10-15 кратного уплотнения информации. Данный стандарт содержит единственный двумерный алгоритм G42D, который отличается от G32D следующими 2-мя характеристиками:

1) в выходном потоке отсутствуют сигналы синхронизации;

2) не используется k-фактор, поэтому в идеале полное кодирова-

ние может быть выполнено для одной верхней строки, остальные будут содержаться в виде строк разницы.

Алгоритм требует больших временных затрат, но при его аппа-

ратной реализации этот недостаток является не существенным.

Арифметическое кодирование

После опубликования алгоритма кодирования Хаффмена появилось множество его модификаций, повышающих те или иные характеристики, послуживших базой для развития эффективных методов сжатия информации. Из подобных методов – энтропийное кодирование, Q-кодирование, арифметическое кодирование – в компьютерной графике

наибольшее распространение получило последнее.Арифметическое кодирование (arithmetic encoding) является одной из разновидностей кодирования Хаффмена, которая позволяет достигать предела сжатия для данной группы методов (предел по тео-

ретическим расчетам составляет 100:1). Однако данный алгоритм запатентован IBM и AT&T, и для его исполнения необходимо лицензированное соглашение.

При арифметическом кодировании происходит отображение каждой уникальной последовательности бит (пикселей) в числовой диапазон [0, 1]. Этот диапазон, соответствующий подстроке бит, представляется затем в виде дробного числа из этого интервала.На практике получается так, что наиболее часто встречается последовательности, которым соответствуют большие интервалы, можно

сопоставить более короткую двоичную дробь. Реже встречающиеся последовательности соответствуют меньшим интервалам и более длинной двоичной дроби.

Рассмотрим работу алгоритма на примере.

Пусть входной поток состоит из шести символов, вероятность появления которых задана в табл.9.4.

Последовательность пикселей, например, ab будет иметь вероятность:

p(ab) = p(a)×p(b) =

=0.05×0.15 = 0.0075.

Таким образом, значение пикселя или группы пикселей можно описать вероятностной характеристикой.

Вероятность появления какой-либо величины можно интерпретировать как интервал на отрезке [0,1] и сложить в некоторой последовательности (рис. 9.3). При этом каждый из входных элементов будет соответствовать интервалу из [0,1].

 

В случае появления элементов потока, имеющих равные вероятностные показатели, в схеме арифметического кодирования им будут соответствовать различные интервалы. В данном примере p(b) = p(c),однако p(b) соответствует интервал [0.05;0.2], а p(c) – [0.2;0.35].

Как и кодирование Хаффмена, арифметическое кодирование наиболее эффективно сжимает потоки с повторяющимися последовательностями. На практике алгоритм арифметического кодирования позволяет достигать сжатия близкого к теоретическим пределам для данной группы методов. Однако, время его работы как при кодировании, так и при декодировании превышает аналогичные показатели алгоритма кодирования Хаффмена. Общими достоинствами алгоритмов сжатия строк бит перемен-

ной длины являются:

1) простота алгоритмов;

2) высокая скорость сжатия.

Недостатки алгоритмов данной группы:

1) применяются для сжатия только черно-белых изображений;

при использовании их для сжатия цветных изображений эффективность резко падает.

2) наиболее эффективные алгоритмы запатентованы.

Конец 69 вопроса.
70.Алгоритмы сжатия со словарем (LZ-алгоритмы).

Базовым алгоритмом для данной группы является алгоритм,предложенный израильскими инженерами Лемпелем и Зивом (Abraham Lempel, Jacob Ziv) в 1977 году (ныне носит название Lempel-Ziv1977, или LZ77). Алгоритмы группы LZ лежат в основе большинства

архиваторов (compress, zoo, lha, pkzip, arj и др.), а также включены в стандарты на факсмодемную связь (V.42 bis) и на язык описания страниц PostScript (level 2).

В 1978 вышла авторская модернизация алгоритма (LZ78), которая была запатентована в 1984 году (патент № 4464650). В этом же году появилась наиболее популярная полностью целочисленная модернизация LZ - LZW, предложенная американским инженером Терри Велчем(Welch T.A.). В 1985 году Велч получил патент на свой вариант алгоритма (№ 4558302), который получил название LZW (Lempel-Ziv-Welch) и был ориентирован на применение в высокоскоростных дисковых контроллерах. В дальнейшем права на этот алгоритм принадлежали ряду фирм (Sperry Corp., Unisys). В настоящее время владельцем является America Online. Именно этот вариант алгоритма стал широко использоваться во многих разработках (в том числе в компьютерной графике – в форматах GIF3 87/89 (CompuServe) и TIFF 5.0 (Aldus Corp.), атакже в стандарте на PostScript (Adobe Systems Corp.), что привело кмногочисленным и долголетним юридическим разбирательствам.

3 GIF - Graphics Interchange Format – графический формат обмена дан-

ными

В 1981 году известным автором архиватора ARC Филом Кацем была разработана другая популярная версия LZ -алгоритма – Deflate, которая не была запатентована и поэтому может использоваться в любых разработках без каких-либо ограничений. Она легла в основу архиваторов семейства pkzip, а также используется при сжатии графической информации в формате PNG 4 Алгоритмы группы LZ называются также алгоритмами со словарями, или алгоритмами подстановок. По входному потоку данных осуществляется построение словаря (таблицы строк, или переводной таблицы), в которой каждому выделенному элементу (слову, строке) сопоставляется код словаря (порядковый номер вхождения в словарь). После этого элементы словаря выделяются их входного потока, а выходной поток формируется из соответствующих кодов словаря. Очевидно, что замена слов и строк на их коды приведет к существенному сжатию информации. Существует множество вариантов выделения строк и формирования словаря. В отдельных случаях бывает необязательно хранить словарь (например, при сжатии текста может использо-

ваться заранее известный словарь).

Конец 70 вопроса.
71.Алгоритм сжатия JPEG.

Алгоритмы сжатия без потерь позволяют сжимать информацию не более чем в 5-10 раз. Последнее время с появлением изображения фотореалистичного качества значительно увеличился объем графической информации. Для получения файлов приемлемого размера показателей сжатия 10:1 оказалось недостаточно. Кроме того, алгоритмы сжатия без потерь имеют следующие недостатки.

1. При повышении цветности (режимы HiColor, TrueColor – соответственно 16 и 24/32 бита/пиксель) данные алгоритмы не только неудовлетворительные результаты сжатия, но могут приводить к отрицательным результатам (к увеличению объемов).

2. Все алгоритмы сжатия без потерь ориентированны на обработку строк битов или строк символов, то есть на обработку одномерных потоков данных. Графические данные и геометрические можно представить в виде двух- или трехмерных потоков информации.

3. Изображения, используемые в компьютерной графике, являются результатом оцифровки аналогичных изображений, то есть представляют собой округленные данные. Поэтому сохранять эти данные с максимальной точностью и применять алгоритмы сжатия без потерь не имеет особого смысла.

Поэтому в конце 70-х годов в рамках объединенной группы экспертов по фотографии (Joint Photographic Expert Group) начались работы по созданию специализированных алгоритмов сжатия для растровых изображений фотореалистичного качества. В середине 80-х годов комитетом CCITT5 и международной организацией стандартов ISO6 были приняты первые версии стандартов, определяющие как сам алгоритм

сжатия, так и формат графического файла JPEG Image File Format

(JFIF). При разработке стандартов был учтен опыт, как инженеров, так и ученых. Последние версии содержат рекомендации по применению, основанные на опыте использования JPEG -сжатия. Стандарт определяет два алгоритма: алгоритм компрессии и декомпрессии.

Алгоритм сжатия (компрессии) состоит из четырех этапов:

1) преобразование цветов;

2) дискретно-косинусное преобразование;

3) квантование;

4) кодирование энтропии.

Алгоритм декомпрессии реализует те же самые этапы в обратном

порядке.

Этап 1. Преобразование цветов

JPEG -преобразование на первом этапе позволяет учитывать особенности человеческого зрения, которые были введены в телевизионных стандартах на цветовые модели (см. раздел 2). В качестве базовой модели цвета используется YUV -модель (Y - яркостная составляющая, U,V -света - разностная составляющая), которая в данном стандарте носит название YCbCr. Преобразование из RGB в YCbCr позволяет выявить данные и сократить их объем. Этот процесс называется подвыборкой, так как различные данные выбирается с различной частотой.Стандарт JPEG рекомендует 2 вида подвыборки: YCbCr 422, YCbCr

411. После прямого преобразования из RGB получается полный сигнал YCbCr 444 (всего 12 выборок) по 4 выборки на каждый цвет. Формат YCbCr 422 позволяет сократить число выборок до 8, а формат YCbCr 411 - до 6. Таким образом, без существенной потери качества мы можем уменьшить объем графических данных в 1,5 или 2 раза.

При пересчете цветового пространства RGB в YCbCr используются следующие формулы:

Y = 0,299R+0,587G+0,114B;

Cb = – 0.1687R – 0.3313G + 0.5B +128;

Cr = 0.5R – 0.4187G – 0.0813B + 128.

На данном этапе происходит потеря информации, но она незначительна, т.к. учитывает особенность восприятия цвета человеком.

Этап 2. Дискретно-косинусное преобразование

Дискретно-косинусное преобразование (ДКП) является разновидностью преобразования Фурье, которое всегда имеет обратное преобразование (ОДКП), что гарантирует процесс компрессии / декомпрессии.

5 CCITT - Comite Conssultatif International de Telegraphique et

Telephonique (фр.) – Консультативный комитет по телеграфии и телефонии

6 ISO - International Standard Organization – Международная организация

стандартизации

Графические изображения рассматриваются как пространственная волна: X,Y-координаты совпадают с высотой и шириной изображения, Z - определяется кодом цвета. ДКП выполняет переход от пространственного представления к спектральному (ОДКП – в обратном направлении). Спектральное представление – ряд Фурье - состоит из гармоник, имеющих различный вес. Первые члены получаемого ряда Фурье соответствуют наиболее

часто встречающимся элементам (цветам), а младшие члены ряда соответствуют редким цветам. Отбрасывая менее значимые гармоники,можно отбирать необходимую степень сжатия при определенных требованиях к качеству сжимаемого изображения. Прямое преобразование Фурье определяется формулой:

Таким образом ДКП преобразует матрицу пикселей р(х,у) в матрицу частотных (спектральных) коэффициентов. Программная реализация достаточно проста. Однако при работе программы, производящей вычисления по формуле ДКП, возникают трудности вычислительного характера. Сложность алгоритма составляет O(N2). Поэтому,

увеличивая значение N, увеличиваем качество изображения (меньше фрагментов, на которое разбивается изображение), но в тоже время увеличивается сложность.

Для упрощения вычислений предварительно рассчитывается ряд коэффициентов и сводятся матрицы. Коэффициенты матрицы определяются по следующим формулам.

1/√N, если i=0;

С (i,j)=

√2/N × cos((2j+1) × i × π / 2N), если i>0.

После вычисления матрицы C формула ДКП принимает матричный вид - преобразование конгруэнтности:

F = C × P × CT

Реализуемый на базе последней формулы алгоритм имеет сложность 0(2N). После выполнения ДКП появляется возможность определить формальным путем, какую часть графической информации можно безболезненно удалить из входного потока. Без проведения спектрального анализа ДКП такой операции выполнить невозможно. На этапе

ДКП потери информации не происходит.

Этап 3. Квантование

Этап ДКП готовит информацию для проведения сжатия с потерями. Такое сжатие осуществляется за счет округления. Округление это уменьшение ненулевых элементов матрицы ДКП F за счет снижения точности. Стандарт JPEG определяет реализацию этой процедуры через матрицу округления. Поступающая на вход преобразования матрица F содержит элементы в следующем порядке: в верхнем левом углу располагаются низ-

кочастотные составляющие (часто встречающиеся цвета). По направлению основной диагонали происходит (сверху вниз) происходит повышение частоты гармоник. В правом нижнем углу находится наиболее высокочастотная составляющая спектра.

Для выполнения процедуры округления осуществляется поэлементное деление матриц F на матрицу квантования М. В результирующей матрице элементы округляются до ближайшего целого. Стандарт JPEG не определяет схемы для выполнения матрицы округления, однако стандарт ISO включает понятие фактор качества Q, через который

определяются элементы матрицы округления M=||mi,j||:

mi,j = 1 + (1 + I + j) × Q.

Чтобы был виден самый редкий элемент (правый нижний), он должен иметь значение fi,j≥16. Если значение fi,j < 16 этот элемент будет обнуляться (аналогично для остальных элементов). Полученные после округления нулевые элементы можно не хранить, уменьшая, таким образом, объем матрицы F. Этап квантования - единственный этап JPEG - сжатия, на котором может происходить существенная потеря информации.

Этап 4. Кодирование энтропии.

На этом этапе выполняется четыре шага, в результате чего степень

сжатия графической информации повышается:

1) кодирование верхнего левого элемента (0,0);

2) построение линейной последовательности;

3) применение метода группового кодирования;

4) сжатие при помощи алгоритмов Хаффмена или арифметического кодирования.

Шаг 1. Соседние блоки размером N*N

чаще всего близки друг другу по цветовым характеристикам. Поэтому имеет смысл кодировать один начальный элемент, а для остальных - определять разницу с первым.

Шаг 2. Линейная последовательность

стирания при помощи обхода модернизированной матрицы F по траектории зигзага

(рис.9.4).

Шаг 3. В полученной строке высока вероятность появления повторяющихся элементов. Поэтому имеет смысл уплотнить ее RLE -алгоритмом.

Шаг 4. После реализации RLE алгоритмов графическая информация может восприниматься как поток бит и подаваться на вход одного из алгоритмо сжатия битовых последовательностей

Конец 71 вопроса.
72.Алгоритм волнового сжатия (вейвлет-преобразование).

Сжатие на основе волнового алгоритма базируется на математическом аппарате волнового преобразования (Wavelet Transforming).Алгоритм разработан в Хьюстонском центре передовых исследований(HARC) наиболее широкое распространение получила дискретная реализация волнового алгоритма ДВП (DWT). ДВП основано на математической модели передачи потока информации через пару фильтров:низкочастотный фильтр (НЧФ) - высокочастотный фильтр (ВЧФ).НЧФ выдает округленную форму информации, а на выходе высокочастотного фильтра получается сигнал разности или детализации. Информация с выхода ВЧФ в свою очередь может поступать на вход следующего ДВП. Существует множество реализаций алгоритма ДВП,основанных на скалярных и векторных представлениях потока информации. Рассмотрим принцип работы ДВП на простейшем примере ДВП - фильтре Хаара (Haare DWT).

Низкочастотная составляющая фильтра Хаара (Low Pass Filter) вычисляется как среднее арифметическое двух соседних этапов потока для i- ого элемента:

gi = (xi + xi + 1)/2.

Высокочастотная составляющая фильтра (High Pass Filter) определяется средняя разность соседних сигналов:

hi=(xi+1 – xi)/2.

При этом сигнал определяется как

xi = gi – hi,

а последующие сигналы определяются xi+1 = gi+hi Выходные последовательности сигналов НЧФ и ВЧФ ({ gi } и { hi }) содержит избыточную (удвоенную) информацию о входном потоке.Для полного описания входной информации можно использовать

либо четные, либо нечетные выборки из входного потока. На практике используются четные выборки, и выходной поток выглядит следующим образом:

〈 (g0, h0), (g2, h2), (g4, h4),... 〉.

По выходному потоку легко восстанавливается входной поток:

x0 = g0 – h0;

x1 = g0 + h0;

x2 = g2 – h2;

x3 = g2 + h2;......

На выходе НЧФ получается первый вариант изображения, имеющее низкое разрешение. Выход ВЧФ добавляет детали в предыдущий поток, тем самым повышает его разрешение (enhancement level). Каждое повторяющееся применение ДВП к выходному сигналу ВЧФ позволяет повышать качество изображения. Само ДВП не сокращает поток информации. Оно выполняет только расположение входного потока по уровню разрешения.

Применяя в дальнейшем операцию квантования (см. описание JPEG -алгоритма) можно удалять избыточную информацию из входного потока (сжатие с потерями). После квантования можно применять алгоритмы кодирования энтропии (алгоритм Хаффмена). Если входной поток состоит из 16-ти байтов, то для выхода НЧФ используется те же 16

байт, а для ВЧФ - 8 байт (скалярное квантование). При последующем применении ДВП выходной поток ВЧФ буде стремиться к нулю.

Данный алгоритм используется в форматах ART и WIF (Wavelet

Image Format), а также в новом варианте стандарта ISO – JPEG 2000.

Средние показатели сжатия формата WIF в 3 раза превосходят показатели алгоритма JPEG, основанного на ДКП. Цветные изображения могут сжиматься в 200-300 раз, черно-белые - 10-30 раз без видимой потери качества

Достоинства волнового преобразования (ДВП):

1) отсутствует блочная структура, характерная для JPEG сжатия;

2) качество изображения при том же коэффициенте сжатия выше, чем JPEG -ДКП;

3) уменьшение объема приводит к повышению скорости передачи по сети.

Недостаток:ДВП размывает изображение, что приводит к эффекту закругления острых контуров изображения

Конец 72 вопроса.
73.Фрактальная математика и фрактальное сжатие.

Понятие фракталов пришло в компьютерную графику из физики и математики. В общем случае фрактальная структура – это структура,обладающая свойством самоподобия.

С физической точки зрения фрактальная структура - это структура вещества, повторяющаяся на как на макро-, так и на микроуровне (например, структура кристалла).

С математической точки зрения фрактал – это геометрической объект, обладающий дробной размерностью (точнее – объект у которого различаются топологическая и хаусдорфова размерности). Базой теории фракталов послужили работы:

1) Гастона Морриса Жули [Джулиа] (Gaston Mourice Julia), который рассматривал множества, состоящие из итераций полиномиальных функций, заданных над комплексными переменными;

2) Феликса Хаусфорда (Felix Hausdorff) в области пространства дробной размерности.

Логическим продолжением этих двух направлений является работа другого французского математика - Бенуа Мандельброта (BenoitMandelbrot). Теория фрактальной геометрии изложена в его известной книге «Фрактальная геометрия природы». Сам термин фрактал (fractus - дробный) был введен Б.Мандельбротом в 1975 году.

В компьютерной графике фрактал - это геометрический объект,построенный на основании базового объекта с использованием одного из законов самоподобия. В простейшем случае законы самоподобия можно выразить при помощи аффинных преобразований (перенос, поворот, масштабирование, трансформация). Совокупность таких преобразований позволяет получить более сложный геометрический объект.

Обычно, геометрические тела имеют размерность, описываемую целыми величинами. Такая размерность называется топологической Dz. Например, для линии Dz =1, для плоских фигур Dz =2, для объемных фигур Dz =3. Если рассматривать более сложные фигуры (траектории движение броуновской частицы), то хаусдорфова размерность может принимать дробное значение Dh (1 < Dh < 2), т.к. линейная траектория (Dz =1)

при t→∞ стремится занять всю плоскость (Dz =2). Разница между двумя показателями размерности называется показателем Херстнона:

H = Dh - Dz

Поэтому с математической точки зрения фрактал - это тот объект,

который имеет различные Dh и Dz, то есть H>0. Комплексные числа во фрактальных множествах Жулиа и Мандельброта позволяют моделировать две координаты:

Z = X + iY (Z - С).

Преобразование Жулиа:

Z=Z2+C (((Z+C)×i+C) ×I …)×Zn+C

Решение задачи фрактального сжатия графической информации в отличие от задачи фрактального построения долгое время оставалось неразрешенной проблемой. В 1988 году Майкл Бансли (Michael F.Barnsley) предложил алгоритм, который стал базовым для всех алгоритмов фрактального сжатия (запатентован фирмой Iterated System). Он за-

ключался в сегментировании исходного изображения и поиске подобных сегментов этого изображения. После выполнения сжатия выходной поток представляет собой поток базовых фрагментов (фракталов) и набор их преобразований, с помощью которых можно восстановить исходное изображение.

В настоящее время существуют две запатентованных технологий фрактального сжатия. Первая из них - FIF (Fractal Image Format) - базируется на основном варианте алгоритма сжатия и используется в Интернете (фирма Genuine Fractals).

Второй вариант Sting является более сложным и включает в себя сжатие без потерь, запатентованный алгоритм фрактального сжатия и кривую качества. Кривая позволяет дозировать объемы данных, необходимых для получения конкретного разрешения. Этот вариант ориентирован не только на просмотр в электронном виде (например, через Internet), но и на высококачественную печать.

Достоинства фрактального метода:

1) высокое сжатие (до 1000 раз);

2) хорошее сжатие сложных объектов;

3) возможность использования любой цветовой схемы;

4) большая скорость декомпрессии;

5) возможность восстановления изображения (масштабирования)

теоретически с любым разрешением.

Недостатки данного метода:

1) значительная длительность процедуры сжатия;

2) плохое качество сжатия регулярных изображений (например,чертежей и схем).

Конец 73 вопроса.
74.Классификация форматов представления графической информации.

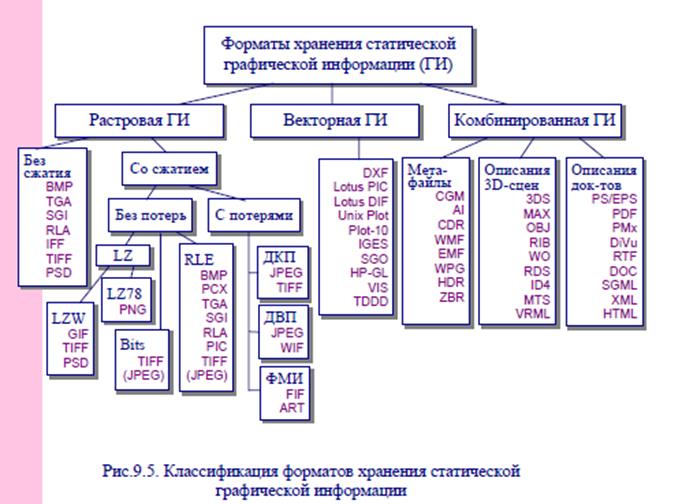
Формат представления и хранения статической графической информации зависит от ее вида. Поэтому различают следующие группы форматов хранения статической графической информации (см.рис.9.5):

• растровые;

• векторные;

• метафайлы;

• описания трехмерных сцен;

• описания документов.

Растровые форматы делятся на форматы поддерживающие сжатие и форматы, хранящие несжатые данные.

Растровые форматы, не использующие сжатие, являются

простейшими и часто используются в качестве базовых форматов

операционных систем. Например, Windows Bitmap (имеет расширение *.BMP), Sun Raster File (*.RAS), SGI Image File Format (*.SGI) и т.п.

Другие варианты подобных форматов обеспечивают быстры доступ к

растровым данным в профессиональных графических редакторах:

Target Image File Format (*.TIF), Truevision Targa (*.TGA), Adobe

Photoshop Document (*.PSD), Wavefront Run-length Encoded ver.A

Format (*.RLA), Amiga Imterchange File Format (*.IFF) и др.

Среди растровых форматов, поддерживающих сжатие, можно выделить форматы, использующие сжатие без потерь и сжатие с потерями. В первом случае могут применяться методы на базе:

- алгоритма группового кодирования (RLE- алгоритма);

- алгоритмов кодирования битовых строк переменной длины;

- алгоритмов сжатия со словарем (группы Лемпела-Зива).

Растровые форматы, поддерживающие сжатие с потерями, делятся

на форматы использующие:

- алгоритмы на базе дискретно-косинусного преобразования (ДКП);

- алгоритмы на базе дискретного волнового преобразования (ДВП);

- алгоритмы на базе фрактальной модели изображения (ФМИ).

Форматы хранения векторных данных в настоящее время

встречаются только в технических системах (CAD/CAM). В офисных

приложениях их вытеснили форматы метафайлов. Базовым считается

формат Computer Graphics Metafile (*.CGM), утвержденный ISO.

Форматы хранения комбинированной информации делятся на

- форматы метафайлов,

- форматы,ориентированные на хранение описаний трехмерных

объектов и сцен, а также

- форматы, предназначенные для описания страниц и документов.

Конец 74 вопроса.
75.Форматы представления видеоданных: Microsoft RIFF AVI, MPEG-1,2,4, QuickTime