Эволюция графического интерфейса операционных систем за последние 30 лет

Эволюция графического интерфейса операционных систем за последние 30 лет

Первый GUI был написан в 70-х годах программистами из центра Xerox Palo Alto Research Center (PARC). Первым ПК с графическим интерфейсом стал Xerox Alto, разработанный в 1973г для некоммерческого использования в университетах.

1981-1985

Xerox 8010 Star (выпущен в 1981г)

Первая система, которая позиционировалась как полностью интегрированная - приложения и интерфейс. Ее назвали “The Xerox Star”, позже переименовав в “ViewPoint”, а потом в “GlobalView”.

Apple Lisa Office System 1 (1983г)

Разработан компанией Apple для офисных компьютеров. Однако, система не вышла в свет будучи поглощенной Mac OS - как более доступной ОС.

В 1983 Lisa обновилась до Lisa OS 2 и Lisa OS 7/7 3.1 в1984, апгрейд затрагивал внутреннюю архитектуру, но не интерфейс.

VisiCorp Visi On (1984)

Первый десктопный интерфейс для IBM PC. Операционка нацеливалась на корпоративных пользователей и стоила довольно приличных денег.. В GUI можно было пользоваться мышью, имелся установщик и справка.

Mac OS System 1.0 (1984)

Первый GUI для компьютеров Macintosh. Окна теперь можно было таскать мышью, а файлы копировать перетаскиванием.

Amiga Workbench 1.0 (1985)

Первый цветной интерфейс (4 цвета: черный, белый, синий, оранжевый), подобие мультизадачности, стерео звук и мультистатусные иконки (выделенная и невыделенная).

Windows 1.0x (1985)

В 1985 году Microsoft тоже выпустила свою систему - Windows 1.0, которая была цветной и с иконками размером 32*32 пикселя. Верхом технического прогресса в те времена считались анимированные стрелки часов в Windows 1.0.

GEM (1985)

GEM (Graphical Environment Manager) был разработан компанией Digital Research, Inc. (DRI). Изначально создавался под ОС CP/M для процессоров Intel 8088 и Motorola 68000, а уже позже был допилен для использования под DOS. <Боьшинство помнит GEM как GUI для компьютеров Atari ST. Также система использовалась в серии Amstrad IBM-совместимых компьютеров.

1986 - 1990

IRIX 3 (разработан в 1986г, самая первая версия - в 1984г)

64-битная операционка IRIX была разработана для UNIX-систем. Из интересного - поддержка векторных иконок - еще задолго до их появления в MacOS.

GEOS (1986)

Система GEOS (Graphic Environment Operating System) была написана компанией Berkeley Softworks (позже - GeoWorks). Изначально была для Commodore 64 и включала графический текстовый редактор geoWrite и программу для рисования geoPaint.

Windows 2.0x (1987)

Окна теперь растягивались, сворачивались, меняли размер и могли накладываться друг на друга.

OS/2 1.x (1988)

OS/2 была совместным детищем IBM и Microsoft, но в 1991году компании рассорились и IBM продолжила разработку OS/2 водиночку. GUI в OS/2 назывался “Менеджер презентаций”. Версия 1.х поддерживала исключительно монохромные иконки фиксированного размера.

NeXTSTEP / OPENSTEP 1.0 (1989)

Стив Джобс в середине 80-х выдвинул идею создания самого лучшего компьютера для исследовательских центров и лабораторий. Позже эта идея воплотилась в жизнь компанией NeXT Computer Inc.

Первый компьютер NeXT был выпущен в 1988г.

Иконки стали больше (48×48) и многоцветнее. GUI изначально был монохромным, а с версии 1.0 стал поддерживать и цветные мониторы.

OS/2 1.20 (1989г)

Следующая версия привнесла некоторые улучшения. Иконки стали выглядеть привлекательнее, а окна - сглаженными.

Windows 3.0 (1990г)

В конце 80-х Microsoft осознала все перспективы графического интерфейса и начала его усиленно развивать.

ОС поддерживала стандартный и расширенный режим, который позволял использовать более 640 KB пространства на жестком диске, что привело к улучшению графики и повышению разрешения изображения до Super VGA 800×600 и 1024×768.

Microsoft наняла Susan Kare в качестве дизайнера для разработки унифицированного стиля графического интерфейса Windows.

1991 - 1995

Amiga Workbench 2.04 (1991г)

Было реализовано множество улучшений в GUI. Изменили цветовую схему, появились зачатки 3D. Рабочий стол мог растягиваться вертикально на несколько мониторов с разным разрешением и глубиной цвета. Разрешением по умолчанию было 640×256, но поддерживались и более высокие.

Mac OS System 7 (1991г)

Первый цветной Mac OS.

Windows 3.1 (1992г)

Эта версия включала предустановленные шрифты TrueType. Также впервые появилась цветовая схема Hotdog Stand для людей с нарушениями зрения.

OS/2 2.0 (1992г)

Это был первый графический интерфейс, получивший международное признание за удобство и доступность. Весь интерфейс был разработан с использованием объектно-ориентированной модели. Каждый файл и папка была объектом, который может быть связан с другими файлами, папками и приложениями.

Windows 95 (1995г)

Интерфейс был полностью переработан по сравнению с предыдущей версией 3.x. Впервые появилась маленькая кнопка "крестик" в правом верхнем углу каждого окна. Также в Windows 95 впервые появилась знаменитая кнопка "Пуск".

1996 - 2000

OS/2 Warp 4 (1996г)

IBM выпустила OS/2 Warp 4, которая привнесла значительные удобства для конечных пользователей.

На рабочем столе размещались иконки, а также можно было создавать свои файлы и папки. Аналогом "Корзины" был shredder, правда он не хранил копии файлов, удаляя их безвозвратно.

Mac OS System 8 (1997г)

По умолчанию использовались 256-цветные изометрические (псевдо-3D) иконки. Серо-платиновый цвет окон в дальнейшем стал торговой маркой операционных систем Apple.

Windows 98 (1998г)

Графический интерфейс стал использовать более 256 цветов. Почти полностью изменился проводник, впервые появился “Active Desktop”.

KDE 1.0 (1998г)

Команда KDE так описала свой проект, выпуская версию 1.0: “KDE - интегрированная с сетью современная среда рабочего стола для рабочих станций UNIX. KDE стремится облегчить использование настольных рабочих станций Unix, также как MacOS или Window95/NT. Это абсолютно свободная и открытая вычислительная платформа, включаюшая исходный код с возможностью любого его изменения.”

BeOs 4.5 (1999г)

Операционная система BeOS была разработана для персональных компьютеров. Изначально была написана компанией Be In в 1991г для использования на компьютерах BeBox. Позднее были внесены новые достижения науки и техники - симметричные мультипроцессорные вычисления, многопоточность, многозадачность и 64-разрядная журналируемая система BFS. GUI разрабатывался по приниципу ясности и чистоты, незагроможденности.

GNOME 1.0 (1999г)

Рабочий стол GNOME, в основном, создавался для Red Hat Linux, а позже перекочевал в другие дистрибутивы Linux.

2001 - 2005

Mac OS X (2001г)

В начале 2000г. Новый интерфейс Aqua, который в 2001 году вошел в состав Mac OS X.

Появились большие сглаженные полупрозрачные пиктограммы размером 128*128 пикселей.

Поначалу многие критиковали этот интерфейс, но потом привыкли, и сейчас этот GUI - основа всех маков.

Windows XP (2001г.)

Майкрософт тоже не осталась в стороне и обновила свою операционку. Интерфейс стал полностью изменяемым, чем не преминули воспользоваться пользователи, сделав множество тем для Windows XP.

KDE 3 (2002г.)

В основном, косметические изменения по сравнению с предыдущей версией.

2007 - 2009

Windows Vista (2007г.)

Microsoft уделал всех. Трехмерная анимация, виджеты, прозрачность и прочие улучшения.

Mac OS X Leopard (2007г.)

6-ое поколение MacOS вышло в 2007 году. В основе по-прежнему осталась Aqua. Новые фичи - трехмерность, новый трехмерный Dock, новая анимация и новая степень интерактивнсти.

GNOME 2.24 (2008г.)

GNOME, как обычно, - нарисовали новые убогие пиктограммы еще больше прежних, обозвав это н.

KDE 4 (2009г.)

Версия 4 K Desktop Environment приобрела многие новые усовершенствования интерфейса, такие как анимация, различные способы управления окнами, поддержка виджетов рабочего стола. Размер значков легко изменяется, любой элемент интерфейса можно настроить по своему вкусу. Новая тема Oxygen - это новые звуки, фотореалистичные иконки, анимация итд.

WINDOWS 7 (2009г.)

ОС

 

3. Устройства ввода графической информации.

Устройства ввода - приборы для занесения (ввода) данных в компьютер во время его работы.

Сканеры(планшетные, слайд-сканеры, барабанные)

По типам сканеры делятся на:
планшетные — для сканирования фотографий или рисунков в отраженном свете. Многие модели этого типа комплектуются слайд-модулями для работы в проходящем свете;
слайд-сканеры — применяются для цифровки негативов и позитивов;
барабанные — обеспечивают наиболее высокое качество сканирования любого материала.

Графический планшет

Roller Mouse

Трекбол

Видео- и Веб-камера

Цифровой фотоаппарат

Плата видеозахвата

Микрофон

Цифровой диктофон

Се́нсорный экран

 

4. Устройства вывода графической информации.

Монитор (дисплей) Монитор (дисплей) компьютера IBM PC предназначен для вывода на экран текстовой и графической информации. Мониторы бывают цветными и монохромными. Они могут работать в одном из двух режимов: текстовом или графическом.

Проектор — световой прибор, перераспределяющий свет лампы с концентрацией светового потока на поверхности малого размера или в малом объёме. Проекторы являются в основном оптико-механическими или оптическо-цифровыми приборами, позволяющими при помощи источника света проецировать изображения объектов на поверхность, расположенную вне прибора — экран. Появление проекционных аппаратов обусловило возникновение кинематографа, относящегося к проекционному искусству.

Принтер Принтеры используют для вывода результатов работы (печати). В настоящее время используется четыре принципиальных схемы нанесения изображения на бумагу: матричный, струйный, лазерный, термопереноса. При матричной печати печатающая головка ударяет иглами по бумаге через красящую ленту, изображение формируется в виде точек. При струйной печати печатающая головка выбрасывает через тонкие сопла краску на бумагу. При лазерной печати лазер поляризует поверхность печатающего барабана, к которой прилипают мелкие частицы красящего порошка. Краска наносится на бумагу и при нагреве впаивается в ее поверхность. При термопереносе нагревается поверхность специальной бумаги, и в точках нагрева изменяется цвет с белого на черный. Для точного начертания схем, чертежей используется графопостроитель. Различаются планшетные и барабанные графопостроители. Компьютер управляет специальным карандашом, который чертит линии по поверхности бумаги. В планшетном карандаш передвигается по поверхности в двух направлениях; в рулонном только поперек рулона бумаги, а бумага перемещается вперед-назад.

 

Графопостроитель

Оптический привод с функцией маркировки дисков

 

5. Типы компьютерной графики.

Компьютерную графику можно классифицировать по нескольким критериям:

1) в зависимости от способа формирования изображений:

 растровая

 векторная

 фрактальная.

 

2) в зависимости от координат измерения (в этом типе компьютерной графики могут сочетаться векторный и растровый способы формирования изображений):

 плоская, двухмерная

 объемная, трехмерная (или 3D-графика).

 

3) в зависимости от специализации в отдельных областях (в этом типе компьютерной графики могут сочетаться векторный и растровый способы формирования изображений):

 инженерная графика

 научная графика

 Web-графика

 компьютерная полиграфия и т.д.

 

Растровая графика.

 

Растровое изображение — изображение, представляющее собой сетку пикселей или цветных точек (обычно прямоугольную) на компьютерном мониторе, бумаге и других отображающих устройствах и материалах (растр).

 

Важными характеристиками изображения являются:

1.количество пикселей — размер. Может указываться отдельно количество пикселей по ширине и высоте (1024×768, 640×480, …) или же, редко, общее количество пикселей (часто измеряется в мегапикселях);

2.количество используемых цветов или глубина цвета (эти характеристики имеют следующую зависимость: N = 2k, где N — количество цветов, а k — глубина цвета);

3.цветовое пространство (цветовая модель) RGB, CMYK, XYZ, YCbCr и др.

4.разрешение — справочная величина, говорящая о рекомендуемом размере пиксела изображения.

 

Растровую графику редактируют с помощью растровых графических редакторов. Создается растровая графика фотоаппаратами, сканерами, непосредственно в растровом редакторе, также путем экспорта из векторного редактора или в виде скриншотов.

 

Пиксел - неделимая точка в графическом изображении. Пиксел характеризуется прямоугольной формой и размерами, определяющими пространственное разрешение изображения

Под растровым (bitmap, raster) понимают способ представления изображения в виде совокупности отдельных точек (пикселов) различных цветов или оттенков (рис.1.1). Это наиболее простой способ представления изображения, потому, что именно таким образом видит его наш глаз.

 

Растровая графика описывает изображения с использованием цветных точек, называемых пикселами, расположенных на сетке. Например, изображение древесного листа описывается конкретным расположением и цветом каждой точки сетки, что создает изображение примерно так же, как в мозаике (фотографии, отсканированные рисунки и т.д.). При редактировании растровой графики Вы редактируете пикселы, а не линии. Растровая графика зависит от разрешения, поскольку информация, описывающая изображение, прикреплена к сетке определенного размера. При редактировании растровой графики, качество ее представления может измениться. В частности, изменение размеров растровой графики может привести к "разлохмачиванию" краев изображения, поскольку пиксели будут перераспределяться на сетке. Вывод растровой графики на устройства с более низким разрешением, чем разрешение самого изображения, понизит его качество.

Применение растровой графики позволяет добиться качественного изображения, фотографического качества. Но за все нужно, платить в данном случае - объемами файлов и трудоемкостью редактирования изображения, приходиться каждую точку подправлять вручную. Даже если Вы при редактировании используете инструменты типа линии или примитивов (овалов, квадратов), то результат представляет собой изменение затронутых данными инструментами пикселей. При изменении размеров, качество изображения ухудшается: при уменьшении - исчезают мелкие детали, а при увеличении картинка может превратиться в набор неряшливых квадратов (увеличенных пикселей). При печати растрового изображения или при просмотре его на средствах имеющих недостаточный разрешающую способность значительно ухудшает восприятие образа.

Рис. 1.1. Пример растрового изображения

 

 

Преимущества и недостатки растровой графики.

Достоинством растрового способа представления изображений является возможность получения фотореалистичного изображения высокого качества в различном цветовом диапазоне. Недостатком – высокая точность и широкий цветовой диапазон требуют увеличения объема файла для хранения изображения и оперативной памяти для его обработки.

 

Достоинства:

1.Растровая графика позволяет создать (воспроизвести) практически любой рисунок, вне зависимости от сложности, в отличие, например, от векторной, где невозможно точно передать эффект перехода от одного цвета к другому без потерь в размере файла.

2.Распространённость — растровая графика используется сейчас практически везде: от маленьких значков до плакатов.

3.Высокая скорость обработки сложных изображений, если не нужно масштабирование.

4.Растровое представление изображения естественно для большинства устройств ввода-вывода графической информации, таких как мониторы (за исключением векторных), матричные и струйные принтеры, цифровые фотоаппараты, сканеры.

 

Недостатки:

1.Большой размер файлов с простыми изображениями.

2.Невозможность идеального масштабирования.

 

6. Типы компьютерной графики.

Компьютерную графику можно классифицировать по нескольким критериям:

1) в зависимости от способа формирования изображений:

 растровая

 векторная

 фрактальная.

 

2) в зависимости от координат измерения (в этом типе компьютерной графики могут сочетаться векторный и растровый способы формирования изображений):

 плоская, двухмерная

 объемная, трехмерная (или 3D-графика).

 

3) в зависимости от специализации в отдельных областях (в этом типе компьютерной графики могут сочетаться векторный и растровый способы формирования изображений):

 инженерная графика

 научная графика

 Web-графика

 компьютерная полиграфия и т.д.

 

Векторная графика.

Кодирование Хаффмана

Один из первых алгоритмов эффективного кодирования информации был предложен Д. А. Хаффманом в 1952 году. Идея алгоритма состоит в следующем: зная вероятности символов в сообщении, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов. Символам с большей вероятностью ставятся в соответствие более короткие коды. Коды Хаффмана обладают свойством префиксности (т.е. ни одно кодовое слово не является префиксом другого), что позволяет однозначно их декодировать.

Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево). ^[1]

1. Символы входного алфавита образуют список свободных узлов. Каждый лист имеет вес, который может быть равен либо вероятности, либо количеству вхождений символа в сжимаемое сообщение.

2. Выбираются два свободных узла дерева с наименьшими весами.

3. Создается их родитель с весом, равным их суммарному весу.

4. Родитель добавляется в список свободных узлов, а два его потомка удаляются из этого списка.

5. Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой — бит 0.

6. Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева.

Допустим, у нас есть следующая таблица частот:

А	Б	В	Г	Д

Этот процесс можно представить как построение дерева, корень которого — символ с суммой вероятностей объединенных символов, получившийся при объединении символов из последнего шага, его n₀ потомков — символы из предыдущего шага и т. д.

Чтобы определить код для каждого из символов, входящих в сообщение, мы должны пройти путь от листа дерева, соответствующего этому символу, до корня дерева, накапливая биты при перемещении по ветвям дерева. Полученная таким образом последовательность битов является кодом данного символа, записанным в обратном порядке.

Для данной таблицы символов коды Хаффмана будут выглядеть следующим образом.

А	Б	В	Г	Д

Поскольку ни один из полученных кодов не является префиксом другого, они могут быть однозначно декодированы при чтении их из потока. Кроме того, наиболее частый символ сообщения А закодирован наименьшим количеством бит, а наиболее редкий символ Д — наибольшим.

При этом общая длина сообщения, состоящего из приведённых в таблице символов, составит 87 бит (в среднем 2,2308 бита на символ). При использовании равномерного кодирования общая длина сообщения составила бы 117 бит (ровно 3 бита на символ). Заметим, что энтропия источника, независимым образом порождающего символы с указанными частотами составляет ~2,1858 бита на символ, т.е. избыточность построенного для такого источника кода Хаффмана, понимаемая, как отличие среднего числа бит на символ от энтропии, составляет менее 0,05 бит на символ.

Классический алгоритм Хаффмана имеет ряд существенных недостатков. Во-первых, для восстановления содержимого сжатого сообщения декодер должен знать таблицу частот, которой пользовался кодер. Следовательно, длина сжатого сообщения увеличивается на длину таблицы частот, которая должна посылаться впереди данных, что может свести на нет все усилия по сжатию сообщения. Кроме того, необходимость наличия полной частотной статистики перед началом собственно кодирования требует двух проходов по сообщению: одного для построения модели сообщения (таблицы частот и Н-дерева), другого для собственно кодирования. Во-вторых, избыточность кодирования обращается в ноль лишь в тех случаях, когда вероятности кодируемых символов являются обратными степенями числа 2. В-третьих, для источника с энтропией, не превышающей 1 (например, для двоичного источника), непосредственное применение кода Хаффмана бессмысленно.

Адаптивное сжатие

Адаптивное сжатие позволяет не передавать модель сообщения вместе с ним самим и ограничиться одним проходом по сообщению как при кодировании, так и при декодировании.

В создании алгоритма адаптивного кодирования Хаффмана наибольшие сложности возникают при разработке процедуры обновления модели очередным символом. Теоретически можно было бы просто вставить внутрь этой процедуры полное построение дерева кодирования Хаффмана, однако, такой алгоритм сжатия имел бы неприемлемо низкое быстродействие, так как построение Н-дерева — это слишком большая работа и производить её при обработке каждого символа неразумно. К счастью, существует способ модифицировать уже существующее Н-дерево так, чтобы отобразить обработку нового символа.

Обновление дерева при считывании очередного символа сообщения состоит из двух операций.

Первая — увеличение веса узлов дерева. Вначале увеличиваем вес листа, соответствующего считанному символу, на единицу. Затем увеличиваем вес родителя, чтобы привести его в соответствие с новыми значениями веса потомков. Этот процесс продолжается до тех пор, пока мы не доберемся до корня дерева. Среднее число операций увеличения веса равно среднему количеству битов, необходимых для того, чтобы закодировать символ.

Вторая операция — перестановка узлов дерева — требуется тогда, когда увеличение веса узла приводит к нарушению свойства упорядоченности, то есть тогда, когда увеличенный вес узла стал больше, чем вес следующего по порядку узла. Если и дальше продолжать обрабатывать увеличение веса, двигаясь к корню дерева, то дерево перестанет быть деревом Хаффмана.

Чтобы сохранить упорядоченность дерева кодирования, алгоритм работает следующим образом. Пусть новый увеличенный вес узла равен W+1. Тогда начинаем двигаться по списку в сторону увеличения веса, пока не найдем последний узел с весом W. Переставим текущий и найденный узлы между собой в списке, восстанавливая таким образом порядок в дереве (при этом родители каждого из узлов тоже изменятся). На этом операция перестановки заканчивается.

После перестановки операция увеличения веса узлов продолжается дальше. Следующий узел, вес которого будет увеличен алгоритмом, — это новый родитель узла, увеличение веса которого вызвало перестановку.

Переполнение

В процессе работы алгоритма сжатия вес узлов в дереве кодирования Хаффмана неуклонно растет. Первая проблема возникает тогда, когда вес корня дерева начинает превосходить вместимость ячейки, в которой он хранится. Как правило, это 16-битовое значение и, следовательно, не может быть больше, чем 65535. Вторая проблема, заслуживающая ещё большего внимания, может возникнуть значительно раньше, когда размер самого длинного кода Хаффмана превосходит вместимость ячейки, которая используется для того, чтобы передать его в выходной поток. Декодеру все равно, какой длины код он декодирует, поскольку он движется сверху вниз по дереву кодирования, выбирая из входного потока по одному биту. Кодер же должен начинать от листа дерева и двигаться вверх к корню, собирая биты, которые нужно передать. Обычно это происходит с переменной типа «целое», и, когда длина кода Хаффмана превосходит размер типа «целое» в битах, наступает переполнение.

Можно доказать, что максимальную длину код Хаффмана для сообщений с одним и тем же входным алфавитом будет иметь, если частоты символов образует последовательность Фибоначчи. Сообщение с частотами символов, равными числам Фибоначчи до Fib (18), — это отличный способ протестировать работу программы сжатия по Хаффману.

 

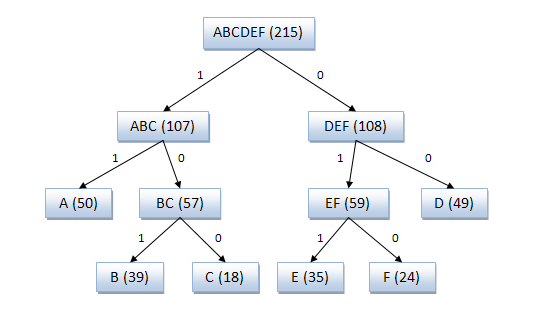
Алгоритм Шеннона-Фано.

Алгоритм Шеннона — Фано — один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано (англ. Fano). Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на несколько лет позже. Алгоритм использует коды переменной длины: часто встречающийся символ кодируется кодом меньшей длины, редко встречающийся — кодом большей длины. Коды Шеннона — Фано префиксные, то есть никакое кодовое слово не является префиксом любого другого. Это свойство позволяет однозначно декодировать любую последовательность кодовых слов.

Кодирование Шеннона — Фано (англ. Shannon-Fano coding) — алгоритм префиксного неоднородного кодирования. Относится к вероятностным методам сжатия (точнее, методам контекстного моделирования нулевого порядка). Подобно алгоритму Хаффмана, алгоритм Шеннона — Фано использует избыточность сообщения, заключённую в неоднородном распределении частот символов его (первичного) алфавита, то есть заменяет коды более частых символов короткими двоичными последовательностями, а коды более редких символов — более длинными двоичными последовательностями.

Алгоритм был независимо друг от друга разработан Шенноном (публикация «Математическая теория связи», 1948 год) и, позже, Фано (опубликовано как технический отчёт).

Основные этапы

1. Символы первичного алфавита m₁ выписывают в порядке убывания вероятностей.

2. Символы полученного алфавита делят на две части, суммарные вероятности символов которых максимально близки друг другу.

3. В префиксном коде для первой части алфавита присваивается двоичная цифра «0», второй части — «1».

4. Полученные части рекурсивно делятся и их частям назначаются соответствующие двоичные цифры в префиксном коде.

Когда размер подалфавита становится равен нулю или единице, то дальнейшего удлинения префиксного кода для соответствующих ему символов первичного алфавита не происходит, таким образом, алгоритм присваивает различным символам префиксные коды разной длины. На шаге деления алфавита существует неоднозначность, так как разность суммарных вероятностей p ₀ − p ₁ может быть одинакова для двух вариантов разделения (учитывая, что все символы первичного алфавита имеют вероятность больше нуля).

[править] Алгоритм вычисления кодов Шеннона — Фано

Код Шеннона — Фано строится с помощью дерева. Построение этого дерева начинается от корня. Всё множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем. Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмана.

При построении кода Шеннона — Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне (n + 1) и привести к неоптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути ещё не гарантирует оптимальности всей совокупности действий. Поэтому код Шеннона — Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннона — Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона — Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, то есть оптимальные коды.

[править] Пример кодового дерева

Исходные символы:

· A (частота встречаемости 50)

· B (частота встречаемости 39)

· C (частота встречаемости 18)

· D (частота встречаемости 49)

· E (частота встречаемости 35)

· F (частота встречаемости 24)

Кодовое дерево

Полученный код: A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.

Кодирование Шеннона — Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев, длина последовательности, сжатой по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях могут сформироваться неоптимальные коды Шеннона — Фано, поэтому более эффективным считается сжатие методом Хаффмана.

 

11. Сжатие графических данных.

Сжатие без потерь (англ. Lossless data compression) — метод сжатия данных: видео, аудио, графики, документов представленных в цифровом виде, при использовании которого закодированные данные могут быть восстановлены с точностью до бита. При этом оригинальные данные полностью восстанавливаются из сжатого состояния. Этот тип сжатия принципиально отличается от сжатия данных с потерями. Для каждого из типов цифровой информации, как правило, существуют свои оптимальные алгоритмы сжатия без потерь.

Сжатие данных без потерь используется во многих приложениях. Например, оно используется во всех файловых архиваторах. Оно также используется как компонент в сжатии с потерями.

Сжатие без потерь используется, когда важна идентичность сжатых данных оригиналу. Обычный пример — исполняемые файлы и исходный код. Некоторые графические файловые форматы, такие как PNG, используют только сжатие без потерь; тогда как другие (TIFF, MNG) или GIF могут использовать сжатие как с потерями, так и без.

АРХИВАЦИЯ И КОМПРЕССИЯ

Как правило, все методы сжатия графических изображений разделяют на две категории: архивацию и компрессию. Под архивацией понимают сжатие информации с возможностью ее дальнейшего восстановления. Компрессия же означает потерю некоторого количества информации об изображении, что естественно приводит к ухудшению качества, но уменьшает объем сохраненных данных. Архивировать можно как растровую, так и векторную графику. Принцип архивации состоит в том, что программа анализирует наличие в сжимаемых данных одинаковых последовательностей и исключает их, записывая вместо повторяющегося фрагмента ссылку на предыдущий и аналогичный ему для того, чтобы была возможность восстановления. Хорошим примером графического объекта с большим количеством одинаковых последовательностей может стать фотография или рисунок с голубым небом в изображении или со сплошной однотонной заливкой. При таком подходе можно восстанавливать нужную информацию без потерь. Компрессия же не гарантирует полного восстановления исходных данных, поэтому ее основная задача - не "убить" что-нибудь очень ценное в погоне за уменьшением объема. Обычно информация, подвергнутая компрессии, занимает значительно меньше объема, чем сохраненная методами архивации. Именно это обстоятельство и оставляет этому методу место под солнцем. Регулирование степени сжатия дает право на выбор: размер выходного файла или сохранение его качества. Рассмотрим несколько алгоритмов сжатия данных, которые не вносят изменений в исходные файлы и гарантируют полное восстановление данных.

В зависимости от того, в каком объекте размещены данные, подлежащие сжатию различают:

1. Сжатие (архивация) файлов: используется для уменьшения размеров файлов при подготовке их к передаче каналами связи или к транспортированию на внешних носителях маленькой емкости;

2. Сжатие (архивация) папок: используется как средство уменьшения объема папок перед долгим хранением, например, при резервном копировании;

3. Сжатие (уплотнение) дисков: используется для повышения эффективности использования дискового просторную путем сжатия данных при записи их на носителе информации (как правило, средствами операционной системы).

 

Алгоритм RLE.

Алгоритм RLE.
Кодирование длин серий (англ. Run-length encoding, RLE) или Кодирование повторов — простой алгоритм сжатия данных, который оперирует сериями данных, то есть последовательностями, в которых один и тот же символ встречается несколько раз подряд. При кодировании строка одинаковых символов, составляющих серию, заменяется строкой, которая содержит сам повторяющийся символ и количество его повторов.
Очевидно, что такое кодирование эффективно для данных, содержащих большое количество серий, например, для простых графических изображений, таких как иконки и графические рисунки. Однако это кодирование плохо подходит для изображений с плавным переходом тонов, таких как фотографии.

Алгоритм LZW.

Алгоритм LZW.
Алгори́тм Ле́мпеля — Зи́ва — Ве́лча (Lempel-Ziv-Welch, LZW) — это универсальный алгоритм сжатия данных без потерь, созданный Абрахамом Лемпелем (англ. Abraham Lempel), Якобом Зивом (англ. Jacob Ziv) и Терри Велчем (англ. Terry Welch). Он был опубликован Велчем в 1984 году, в качестве улучшенной реализации алгоритма LZ78, опубликованного Лемпелем и Зивом в1978 году. Алгоритм разработан так, чтобы его можно было быстро реализовать, но он не обязательно оптимален, поскольку он не проводит никакого анализа входных данных.

1. Инициализация словаря всеми возможными односимвольными фразами. Инициализация входной фразы w первым символом сообщения.
2. Найти в словаре строку W наибольшей длины, которая совпадает с последними принятыми символами.
3. Считать очередной символ K из кодируемого сообщения.
4. Если КОНЕЦ_СООБЩЕНИЯ, то выдать код для W, иначе
5. Если фраза WK уже есть в словаре, присвоить входной фразе W значение WK и перейти к Шагу 3, иначе выдать код W, добавить WK в словарь, присвоить входной фразе W значение K и перейти к Шагу 3.
6. Конец
На момент своего появления алгоритм LZW давал лучший коэффициент сжатия, для большинства приложений, чем любой другой хорошо известный метод того времени. Он стал первым широко используемым на компьютерах методом сжатия данных.
Алгоритм был реализован в программе compress, которая стала более или менее стандартной утилитой Unix-систем приблизительно в 1986 году. Несколько других популярных утилит-архиваторов также используют этот метод или близкие к нему.
В 1987 году алгоритм стал частью стандарта на формат изображений GIF. Он также может (опционально) использоваться в форматеTIFF.
В настоящее время, алгоритм содержится в стандарте PDF.

 

12. Форматы графических файлов. Растровые форматы.

Форматы графических файлов

GIF - Compuserve Graphics Interchange Format

TIFF - Aldus & Microsoft Tag Image File Format

РСХ - ZSoft РС Paintbrush format

RLE - Compuserve & Teletext Run Length Encoded

ВМР - Microsoft Windows BitMaP

LBM - Deluxe Paint format

PIC - Pictor/PC Paint forma