
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрица поворота в двумерном пространствеСодержание книги
Поиск на нашем сайте
В двумерном пространстве поворот можно описать одним углом
Поворот выполняется путём умножения матрицы поворота на вектор-столбец, описывающий вращаемую точку:
Координаты (x',y') в результате поворота точки (x,y) имеют вид:
Положительным углам при этом соответствует вращение вектора против часовой стрелки в обычной, правосторонней системе координат, и по часовой стрелке в левосторонней системе координат. [править] Матрица поворота в трёхмерном пространстве Матрицами вращения вокруг оси декартовой системы координат на угол α в трёхмерном пространстве являются: · Вращение вокруг оси x:
· Вращение вокруг оси y:
· Вращение вокруг оси z:
Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть на плоскость вращении со стороны полупространства, где значения координат оси, вокруг которой осуществляется поворот, положительные. Правая система координат связана с выбором правого базиса (см. правило буравчика).
Свойства матрицы поворота. Свойства матрицы поворота Если · · · · · · если строки (или столбцы матрицы) рассматривать как координаты векторов o o o · Матрица обратного поворота получается обычным транспонированием матрицы прямого поворота, т. о.
24. Алгоритм Брезенхема для растеризации отрезка. Алгоритм Брезенхе́ма (англ. Bresenham's line algorithm) — это алгоритм, определяющий, какие точки двумерного растра нужно закрасить, чтобы получить близкое приближение прямой линии между двумя заданными точками. Это один из старейших алгоритмов в машинной графике — он был разработан Джеком Е. Брезенхэмом (Jack E. Bresenham) в компании IBM в 1962 году. Алгоритм широко используется, в частности, для рисования линий на экране компьютера. Существует обобщение алгоритма Брезенхэма для построения кривых 2-го порядка. Алгоритм Отрезок проводится между двумя точками — (x 0, y 0) и (x 1, y 1), где в этих парах указаны колонка и строка, соответственно, номера которых растут вправо и вниз. Сначала мы будем предполагать, что наша линия идёт вниз и вправо, причём горизонтальное расстояние x 1 − x 0 превосходит вертикальное y 1 − y 0, т.е. наклон линии от горизонтали — менее 45°. Наша цель состоит в том, чтобы для каждой колонки x между x 0 и x 1, определить, какая строка y ближе всего к линии, и нарисовать точку (x, y). Общая формула линии между двумя точками:
Поскольку мы знаем колонку x, то строка y получается округлением к целому следующего значения:
Однако, вычислять точное значение этого выражения нет необходимости. Достаточно заметить, что y растёт от y 0 и за каждый шаг мы добавляем к x единицу и добавляем к y значение наклона
которое можно вычислить заранее. Более того, на каждом шаге мы делаем одно из двух: либо сохраняем тот же y, либо увеличиваем его на 1. Что из этих двух выбрать — можно решить, отслеживая значение ошибки, которое означает — вертикальное расстояние между текущим значением y и точным значением y для текущего x. Всякий раз, когда мы увеличиваем x, мы увеличиваем значение ошибки на величину наклона s, приведённую выше. Если ошибка превысила 0.5, линия стала ближе к следующему y, поэтому мы увеличиваем y на единицу, одновременно уменьшая значение ошибки на 1. В реализации алгоритма, приведённой ниже, plot(x,y) рисует точку, а abs возвращает абсолютную величину числа: function line(x0, x1, y0, y1) int deltax:= abs(x1 - x0) int deltay:= abs(y1 - y0) real error:= 0 real deltaerr:= deltay / deltax int y:= y0 for x from x0 to x1 plot(x,y) error:= error + deltaerr if error >= 0.5 y:= y + 1 error:= error - 1.0Проблема такого подхода — в том, что с вещественными величинами, такими как error и deltaerr, компьютеры работают относительно медленно. Кроме того, при вычислениях с плавающей точкой может накапливаться ошибка. По этим причинам, лучше работать только с целыми числами. Это можно сделать, если умножить все используемые вещественные величины на deltax. Единственная проблема — с константой 0.5 — но в данном случае достаточно умножить обе части неравенства на 2. Получаем следующий код: function line(x0, x1, y0, y1) int deltax:= abs(x1 - x0) int deltay:= abs(y1 - y0) int error:= 0 int deltaerr:= deltay int y:= y0 for x from x0 to x1 plot(x,y) error:= error + deltaerr if 2 * error >= deltax y:= y + 1 error:= error - deltaxУмножение на 2 для целых чисел реализуется битовым сдвигом влево. Теперь мы можем быстро рисовать линии, направленные вправо-вниз с величиной наклона меньше 1. Осталось распространить алгоритм на рисование во всех направлениях. Это достигается за счёт зеркальных отражений, т.е. заменой знака (шаг в 1 заменяется на -1), обменом переменных x и y, обменом координат начала отрезка с координатами конца. [править] Рисование линий Реализация на C++: void drawLine(int x1, int y1, int x2, int y2){ int deltaX = abs(x2 - x1); int deltaY = abs(y2 - y1); int signX = x1 < x2? 1: -1; int signY = y1 < y2? 1: -1; int error = deltaX - deltaY; for (;;) { setPixel(x1, y1); if(x1 == x2 && y1 == y2) break; int error2 = error * 2; if(error2 > -deltaY) { error -= deltaY; x1 += signX; } if(error2 < deltaX) { error += deltaX; y1 += signY; } }}
25. Алгоритм Брезенхема для растеризации окружности. Рисование окружностей Также существует алгоритм Брезенхэма для рисования окружностей. По методу построения он похож на рисование линии. В этом алгоритме строится дуга окружности для первого квадранта, а координаты точек окружности для остальных квадрантов получаются симметрично. На каждом шаге алгоритма рассматриваются три пикселя, и из них выбирается наиболее подходящий путём сравнения расстояний от центра до выбранного пикселя с радиусом окружности. // R - радиус, X1, Y1 - координаты центра int x:= 0 int y:= R int delta:= 2 - 2 * R int error:= 0 while (y >= 0) drawpixel(X1 + x, Y1 + y) drawpixel(X1 + x, Y1 - y) drawpixel(X1 - x, Y1 + y) drawpixel(X1 - x, Y1 - y) error = 2 * (delta + y) - 1 if ((delta < 0) && (error <= 0)) delta += 2 * ++x + 1 continue error = 2 * (delta - x) - 1 if ((delta > 0) && (error > 0)) delta += 1 - 2 * --y continue x++ delta += 2 * (x - y) y--
Алгоритм сглаживания Ву. Алгоритм Ву — это алгоритм разложения отрезка в растр со сглаживанием. Был предложен У Сяолинем (Xiaolin Wu, отсюда устоявшееся в русском языке название алгоритма) в статье, опубликованной журналом Computer Graphics в июле 1991 года. Алгоритм сочетает высококачественное устранение ступенчатости и скорость, близкую к скорости алгоритма Брезенхема без сглаживания. Алгоритм Горизонтальные и вертикальные линии не требуют никакого сглаживания, поэтому их рисование выполняется отдельно. Для остальных линий алгоритм Ву проходит их вдоль основной оси, подбирая координаты по неосновной оси аналогично алгоритму Брезенхема. Отличие состоит в том, что в алгоритме Ву на каждом шаге устанавливается не одна, а две точки. Например, если основной осью является Х, то рассматриваются точки с координатами (х, у) и (х, у+1). В зависимости от величины ошибки, которая показывает как далеко ушли пиксели от идеальной линии по неосновной оси, распределяется интенсивность между этими двумя точками. Чем больше удалена точка от идеальной линии, тем меньше ее интенсивность. Значения интенсивности двух пикселей всегда дают в сумме единицу, то есть это интенсивность одного пикселя, в точности попавшего на идеальную линию. Такое распределение придаст линии одинаковую интенсивность на всем ее протяжении, создавая при этом иллюзию, что точки расположены вдоль линии не по две, а по одной.
Результат работы алгоритма Реализация в псевдокоде (только для линии по x): function plot(x, y, c) is // рисует точку с координатами (x, y) // и яркостью c (где 0 ≤ c ≤ 1) function ipart(x) is return целая часть от x function round(x) is return ipart(x + 0.5) // округление до ближайшего целого function fpart(x) is return дробная часть x function draw_line(x1,y1,x2,y2) is if x2 < x1 then swap (x1, x2) swap (y1, y2) end if dx:= x2 - x1 dy:= y2 - y1 gradient:= dy ÷ dx // обработать начальную точку xend:= round(x1) yend:= y1 + gradient × (xend - x1) xgap:= 1 - fpart(x1 + 0.5) xpxl1:= xend // будет использоваться в основном цикле ypxl1:= ipart(yend) plot(xpxl1, ypxl1, 1 - fpart(yend) × xgap) plot(xpxl1, ypxl1 + 1, fpart(yend) × xgap) intery:= yend + gradient // первое y-пересечение для цикла // обработать конечную точку xend:= round(x2) yend:= y2 + gradient × (xend - x2) xgap:= fpart(x2 + 0.5) xpxl2:= xend // будет использоваться в основном цикле ypxl2:= ipart(yend) plot(xpxl2, ypxl2, 1 - fpart(yend) × xgap) plot(xpxl2, ypxl2 + 1, fpart(yend) × xgap) // основной цикл for x from xpxl1 + 1 to xpxl2 - 1 do plot(x, ipart(intery), 1 - fpart(intery)) plot(x, ipart(intery) + 1, fpart(intery)) intery:= intery + gradient repeatend function
26. Алгоритмы закрашивания. Алгоритм закрашивания Алгоритм закрашивания очень часто используется в компьютерной графике для закрашивания фигур имеющих границы. Так же этот алгоритм может иметь и другое применение например его можно использовать для нахождения центра масс тела по его изображению. Алгоритмы двумерной растровой графики: закрашивание
Простое рекурсивное заполнение.
Procedure PixelFill (x, y, BColor, Color: Integer); {x, y – координаты затравочной точки, BColor – цвет границы, Color – цвет заполнения} Var C: Integer; Begin C:=GetPixel (x,y) {анализируем текущий цвет пикселя} if (C<>BColor) and (C<>Color) then Begin PutPixel (x, y, Color); PixelFill (x+1, y, BColor, Color); PixelFill (x, y+1, BColor, Color); PixelFill (x-1, y, BColor, Color); PixelFill (x, y-1, BColor, Color); End; End; Этот алгоритм не оптимизирован относительно использования стековой памяти и является одним из самых медленных алгоритмов закрашивания (в среднем только один из четырёх вызовов используется для закрашивания). Алгоритм не может заполнить области, ограниченные цветом заполнения. Можно построить подобный алгоритм и без рекурсии, если вместо стека использовать массивы. Алгоритм закрашивания линиями.
2. Находятся xL и xR – левая и правая границы, между которыми проводится текущая горизонтальная линия. 3. Делается приращение у=у+dir и, между xL и xR, анализируется цвет пикселей над линией. Если он не совпадает с цветом заполнения, процедура LineFill вызывается рекурсивно с dir = 1 и xPL = xL, xLR = xR. 4. Делается приращение y=y–dir и, начиная от xL до предыдущего значения xPL анализируется цвет пикселей под линией. Если цвет пикселя отличается от цвета заполнения, процедура вызывается рекурсивно с dir = –1 и xPL = xL, xPR = xR. 5. Продолжая по той же горизонтали от предыдущего xPR до xR анализируется цвет под линией. Если цвет какого-либо пикселя отличается от цвета заполнения, процедура вызывается рекурсивно с dir = –1 и xPL = xL, xPR = xR. void LineFill (int x, int y, int dir, int xPL, int xPR) { int xL=x; xR=x; int color; // в этой переменной будет храниться цвет пикселя // УСТАНАВЛИВАЕМ ТЕКУЩИЕ ГРАНИЦЫ xL И xR do color = GetPixel (--xL,y); // xL=xL-1 помещается в вызов функции while (color!= bcolor); // bcolor – цвет границы do color = GetPixel (++xR,y); while (color!=bcolor); xL++; xR--; Line (xL,y, xR,y, Mycolor); //это может быть любая функция рисования линии // АНАЛИЗИРУЕМ ПИКСЕЛИ НАД ЛИНИЕЙ for (x=xL; x<=xR; x++) { color = GetPixel (x, y+dir); if (color!=bcolor) x = LineFill (x, y+dir, dir, xL, xR); } // АНАЛИЗИРУЕМ ПИКСЕЛИ ПОД ЛИНИЕЙ СЛЕВА for (x=xL; x<=xPL; x++) { color = GetPixel (x, y-dir); if (color!=bcolor) x = LineFill (x, y–dir, –dir, xL, xR); } // АНАЛИЗИРУЕМ ПИКСЕЛИ ПОД ЛИНИЕЙ СПРАВА for (x=xPR; x<=xR; x++) { color = GetPixel (x, y-dir); if (color!=bcolor) x = LineFill (x, y–dir, –dir, xL, xR); } } В программах функция LineFill вызывается следующим образом: LineFill (xst, yst, 1, xst, xst); Совершенно очевидно, что существуют и другие эффективные алгоритмы заполнения. Например, алгоритмы заполнения, которые используют математическое описание контура, связаны с конкретной формой того полигона, который должен быть заполнен (например, прямоугольник или окружность). При этом контур может совсем не выводиться в растр. При этом в качестве заполнения легко использовать какую-либо текстуру.
27. Алгоритм отсечения отрезка Сазерленда-Коэна. Алгоритм Коэна — Сазерленда (англ. Cohen-Sutherland) — алгоритм отсечения отрезков, то есть алгоритм, позволяющий определить часть отрезка, которая пересекает прямоугольник. Был разработан Дэном Коэном и Айвеном Сазерлендом в Гарварде в 1966—1968 гг., и опубликован на конференции AFIPS в 1968.[1][2] Описание алгоритма
Алгоритм разделяет плоскость на 9 частей прямыми, которые образуют стороны прямоугольника. Каждой из 9 частей присваивается четырёхбитный код. Биты (от младшего до старшего) значат «левее», «правее», «ниже», «выше». Иными словами, у тех трёх частей плоскости, которые слева от прямоугольника, младший бит равен 1, и так далее. Алгоритм определяет код конечных точек отрезка. Если оба кода равны нулю, то отрезок полностью находится в прямоугольнике. Если битовое И кодов не равно нулю, то отрезок не пересекает прямоугольник (т.к. это значит, что обе конечные точки отрезка находятся с одной стороны прямоугольника). В прочих случаях, алгоритм выбирает конечную точку, находящуюся вне прямоугольника, находит ближайшую к ней точку пересечения отрезка с одной из линий, образующей стороны прямоугольника, и использует эту точку пересечения как новую конечную точку отрезка. Укороченный отрезок снова пропускается через алгоритм. Реализация алгоритма для трёхмерной модели идентична двумерной реализации, за исключением того, что вместо четырёхразрядного кода применяется шестиразрядный (дополнительные два бита глубины).
28. Алгоритм разбиения средней точкой.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 5765; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.184.125 (0.008 с.) |

 со следующей матрицей линейного преобразования в декартовой системе координат:
со следующей матрицей линейного преобразования в декартовой системе координат:
 .
. ,
, .
. ,
, ,
, .
. — матрица, задающая поворот вокруг оси
— матрица, задающая поворот вокруг оси  на угол ϕ, то:
на угол ϕ, то: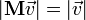

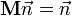

 (след матрицы вращения)
(след матрицы вращения)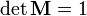 (матрица имеет единичный определитель).
(матрица имеет единичный определитель). , то верны следующие соотношения):
, то верны следующие соотношения):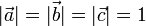

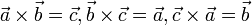
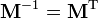 .
.










