
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Декартова (Картезианская) система координатСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Структура взаимосвязей между системами координат
Базовая косоугольная система координат Координаты определяются осями (х – ось абсцисс, у - ось ординат) Расстояние определяется проекциями Полярная система координат
Точка О – полюс, M(r, Соответственно
Цилиндрические координаты
Есть некая плоскость Z проекция на точку M
Сферические системы координат
угол Соответственно
1. 2. 3.
Косоугольная система координат
0 в середине экрана у Картезианской системе координат. (.)
Двумерная (2D — от англ. two dimensions — «два измерения») компьютерная графика классифицируется по типу представления графической информации, и следующими из него алгоритмами обработки изображений. Обычно компьютерную графику разделяют на векторную и растровую, хотя обособляют ещё и фрактальный тип представления изображений. Трёхмерная графика (3D — от англ. three dimensions — «три измерения») оперирует с объектами в трёхмерном пространстве. Обычно результаты представляют собой плоскую картинку, проекцию. Трёхмерная компьютерная графика широко используется в кино, компьютерных играх. Однородные координаты. Однородные координаты Определение. Однородные координаты — координаты, обладающие тем свойством, что определяемый ими объект не меняется при умножении всех координат на одно и то же число. Однородными координатами вектора (х, у, z) является тройка чисел (x', y', z', w), где х = х' / w, у = y' / w, z = z' / w, а w — некоторое вещественное число (случай, когда w = 0 является особым). Данные координаты не позволяют однозначно задать точку пространства. Например, (1, 1, 1, 1) и (2, 2, 2, 2) задают одну и ту же точку (1, 1, 1). При переходе к однородным координатам для точки с координатами (x, y, z) предлагается взять набор (x, y, z, 1).В процессе преобразований координата w может меняться. Обратный переход к декартовым координатам осуществляется посредством деления на w-координату. ИЛИ Однородные координаты - это математический механизм, связанный с определением положения точек в пространстве. Привычный аппарат декартовых координат, не подходит для решения некоторых важных задач в силу следующих соображений: · В декартовых координатах невозможно описать бесконечно удаленную точку. А многие математические и геометрические концепции значительно упрощаются, если в них используется понятие бесконечности. Например, "бесконечно удаленный источник света". · С точки зрения алгебраических операций, декартовы координаты не позволяют провести различия межу точками и векторами в пространстве. Действительно, (1,2,5) - это направление или точка? · Невозможно использовать унифицированный механизм работы с матрицами для выражения преобразований точек. С помощью матриц 3x3 можно описать вращение и масштабирование, однако описать смещение (x=x+a) нельзя. · Аналогично, декартовы координаты не позволяют использовать матричную запись для задания перспективного преобразования (проекции) точек. Матрица переноса. Перенос Рассмотрим элементарные геометрические преобразования (двухмерные и трехмерные), применяемые в машинной графике. Эти преобразования основаны на матричных операциях. Рассмотрим преобразования на плоскости - перенос, масштабирование, поворот. Точку на плоскости можно перенести в новые позиции путем добавления к координатам этих точек констант переноса. х' = х + Dx у' = у + Dy Определяем векторы строки Р=[х,у] Р'=[х',у'] T=[Dx,Dy] Сдвиг точки в векторной форме [x',y']=[x,y]+[Dx,Dy] Или более кратко Р' =Р+Т Объект можно перенести, применяя это выражение к каждой точке объекта. Однако для отрезка достаточно применить этот процесс только к его концевым точкам. Это справедливо и для масштабирования и для поворота. Уравнение переноса Пользуясь однородными координатами можно записать в виде однотипных матричных выражений все три вида преобразований. |1 0 0 | [x'y'1]=[x,y,1] |0 1 0 | |Dx Dy 1 |ил Р' =Р . Т(Dx,Dy) Если перенести точку на (Dx1,Dy1), а затем на (Dx2,Dy2), то последовательным применением преобразования переноса суммарный перенос запишется в виде матрицы | 1 0 0 | | 0 1 0 | |Dx1+Dx2 Dy1+Dy2 1 |Х мерный перенос Трехмертные операции являются простым расширением двумерных.
Свойства матрицы переноса. Матрица перехода является невырожденной. То есть определитель этой матрицы не равен нулю.
23. Матрица масштабирования. Масштабирование Для масштабирования объекта каждую точку необходимо растянуть в Sx раз по оси х и в Sy раз по оси у. х' = х . Sx у' = у . Sy Определяя
или P'=P . S
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.82.60 (0.007 с.) |




 - полярный угол, r – полярное расстояние.
- полярный угол, r – полярное расстояние.

 угол
угол  - полярное расстояние
- полярное расстояние


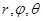 )
)
 )
)







