Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение систем линейных уравнений. Теорема Кронекера – КапеллиСодержание книги
Поиск на нашем сайте
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ МАТРИЦЫ Основные понятия Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины). Матрица записывается в виде А = где ί = 1,2,3,…, m − номер строки, j = 1,2,3,…, n − номер столбца. Числа Диагональ квадратной матрицы, составленная из элементов a 11, a 22, …, ann, называется главной диагональю. Квадратная матрица называется единичной, если на главной диагонали у нее стоят единицы, а остальные элементы – нули. Матрица, все элементы которой равны нулю, называется нулевой. Матрица, содержащая один столбец или одну строку, называется вектором. Пусть дана произвольная матрица
Матрица Заметим, что Матрицы А и В одинаковых размеров n ´ m с элементами называются равными, если
Действия над матрицами Сложение Операция сложения матриц вводится только для матриц одинаковых размеров. Суммой двух матриц А и В одинаковых размеров n ´ m с элементами Определенное таким образом сложение будет, очевидно, коммутативным и ассоциативным. Разность матриц А – В можно определить так: А – B = A + (– B). Умножение на число Произведением матрицы А = ( Операции сложения матриц и умножения матрицы на число обладают следующими свойствами: 1. А + В = В + А; 5. 1 · A = A;
2. А + (B + C) = (A + B) + C; 6. α ·(A + B) = αA + αB; 3. A + O = A; 7. (α + β) · A = αA + βA; 4. A – A = O; 8. α · (βA) = (αβ) · A, где А, B, C − матрицы, α и β − числа. Элементарные преобразования матриц Элементарными преобразованиями матриц являются: · перестановка местами двух параллельных рядов матрицы; · умножение всех элементов ряда матрицы на число, отличное от нуля; · прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число. Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований, А ~ В. Произведение матриц Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы А размера m ´ n с элементами В размера n ´ p с элементами
где i = 1, 2, …, m, j = 1, 2, …, p.
Пример1.1.
Матрицы А и В называются перестановочными, если АВ = ВА. Умножение матриц обладает следующими свойствами, если суммы и произведения матриц имеют смысл: 1. А × В ¹ В × А; 4. (В + С) × А = В × А + С × А; 2. А× (В × С) = (А × В) × С; 5. α · (AВ) = (αА) · В. 3. А × (В + С)= А × В + А × С; Для операции транспонирования верны свойства: 1. 2. ОПРЕДЕЛИТЕЛИ Основные понятия Квадратной матрице А порядка п можно сопоставить число det A (или | А |, или ∆), называемое ее определителем (детерминантом), следующим образом: det A = Основываясь на определении, запишем явные формулы для вычисления определителей второго и третьего порядков: det A =
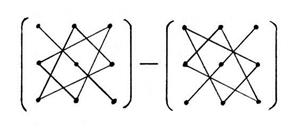
det A = Пример2.1: 1. 2. Выражение определителя третьего порядка является достаточно громоздким. Для запоминания формулы существует удобный способ, который схематично можно изобразить следующим образом:
Свойства определителей Сформулируем основные свойства определителей, присущие определителям всех порядков. 1. Определитель не изменится, если его строки заменить столбцами, и наоборот. 2. При перестановке двух строк (столбцов) определитель меняет знак. 3. Определитель, имеющий две одинаковые строки, равен нулю.
4. Общий множитель элементов какой-либо строки (столбца) определителя можно вынести за знак определителя. 5. Если элементы какой-либо строки (столбца) определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей. 6. Определитель не изменится, если к элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на любое число. Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения. Минором Алгебраическим дополнением элемента
7. Определитель равен сумме произведений элементов некоторой строки (столбца) на соответствующие им алгебраические дополнения.
Эти формулы называются формулами разложения определителя по i-й строке и по j-му столбцу, соответственно. В качестве примера запишем формулу разложения определителя третьего порядка по первой строке: ∆ = Заметим, что при использовании формулы разложения определителя по строке (или по столбцу) удобно иметь в этой строке (в этом столбце) много элементов, равных нулю (тогда соответствующие им миноры не надо будет вычислять). Поэтому полезно предварительно так преобразовать определитель, чтобы в одной из строк (или в одном из столбцов) только один элемент остался, отличный от нуля. Пример2.2. Вычислить определитель четвертого порядка:
Решение. Выполним следующее преобразование: умножим второй столбец на (–4) и прибавим его к третьему столбцу. Затем разложим полученный определитель по первой строке. Получим:
Умножая первую строку на (–2) и прибавляя ее ко второй строке, затем, раскладывая полученный определитель по первому столбцу, вычисляем:
8. Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю.
НЕВЫРОЖДЕННЫЕ МАТРИЦЫ Основные понятия Пусть А − квадратная матрица п -го порядка
Квадратная матрица А называется невырожденной, если ее определитель не равен нулю: ∆ = det A ≠ 0, и вырожденной – в противном случае. Матрицей, союзной (присоединенной) к матрице А, называется матрица
составленная из алгебраических дополнений к элементам матрицы А, причем алгебраическое дополнение Матрица
где Е − единичная матрица того же порядка, что и матрица А. Матрица
Обратная матрица Теорема 3.1 ( О существовании обратной матрицы ). Если А – невырожденная квадратная матрица, то она имеет единственную обратную матрицу, получающуюся из присоединенной
Проведем доказательство для случая матрицы 3-го порядка. Пусть
Составим союзную матрицу
и найдем произведение матриц А и А ∙
т.е. А ∙
Аналогично убеждаемся, что
Равенства (3.2) и (3.3) перепишем в виде
Сравнивая полученные результаты с определением (3.1), получаем
Отметим свойства обратной матрицы: 1. det( 2. 3.
Ранг матрицы Рассмотрим матрицу А размера m×n.
Выделим в ней k строк и k столбцов (k ≤ min (m; n)). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k -го порядка. Все такие определители называются минорами этой матрицы. В матрице А пунктиром выделен минор 2-го порядка. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается r, r (A) или rang A. Очевидно, что 0 ≤ r ≤ min (m; n), где min (m; n) – меньшее из чисел m и n. Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров. Свойства ранга матрицы: 1. При транспонировании матрицы ее ранг не меняется. 2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится. 3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ Основные понятия Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида
где Такую систему удобно записывать в компактной матричной форме
Коэффициенты этих уравнений записываются в виде матрицы А, называемой основной матрицей системы, а числа, стоящие в правой части системы, образуют столбец В, называемый столбцом свободных членов:
Расширенной матрицей системы называется матрица
Совокупность чисел Системы, не имеющие решения, называются несовместными. Системы, имеющие решения, называются совместными. Заметим, что система может иметь единственное решение, а может иметь бесконечно много решений. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением. Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Эквивалентные системы получаются при элементарных преобразованиях системы при условии, что преобразования выполняются над строками матрицы. Система линейных уравнений называется однородной, если все свободные члены равны нулю:
Одна из задач линейной алгебры состоит в том, чтобы найти метод, позволяющий определить, совместна система или нет, а в случае совместности найти все решения системы. Изложенная выше теория определителей позволяет исследовать на совместность системы, имеющие одинаковое количество уравнений и неизвестных. Общее уравнение прямой. Уравнение вида Ах + Ву + С = 0. (3.1) называется общим уравнением прямой. Коэффициенты А и В в уравнении (3.1) являются координатами вектора нормали к этой прямой. Неполные уравнения прямой. Общее уравнение прямой (3.1) называется неполным, если хотя бы один из коэффициентов А, В или С равен нулю. В противном случае уравнение называется полным. Рассмотрим различные виды неполных уравнений прямой. 1) С = 0, уравнение Ах + Ву = 0 определяет прямую, проходящую через начало координат; 2) В = 0, уравнение Ах + С = 0 определяет прямую, параллельную оси Оу, так как нормаль к этой прямой п = (А, 0) является нормалью и к оси Оу; 3) А = 0, уравнение Ву + С = 0 определяет прямую, параллельную оси Ох, так как нормаль к этой прямой п = (0, В) является нормалью и к оси Ох; 4) В = 0, С = 0, уравнение Ах = 0 равносильно уравнению х = 0 и определяет ось Оу; 5) А = 0, С = 0, уравнение Ву = 0 равносильно уравнению у = 0 и определяет ось Ох. Виды уравнений плоскости
Определение 3.2. Уравнение вида Ах + Ву + Сz + D = 0, где А, В, C и D – некоторые числа, называется уравнением первой степени. Теорема 3.1. В декартовой системе координат любое уравнение первой степени определяет некоторую плоскость и, наоборот, любая плоскость в декартовой системе координат определяется уравнением первой степени. Рассмотрим различные виды уравнений плоскости. Общее уравнение плоскости. Уравнение вида Ах + Ву + Сz + D = 0 (3.20) называется общим уравнением плоскости. Геометрический смысл коэффициентов А, В и С в уравнении (3.20): они являются координатами вектора нормали n к этой плоскости, т.е. вектора, перпендикулярного данной плоскости. Общие уравнения прямой. Прямую можно определить как линию пересечения двух плоскостей. Это и будут общие уравнения прямой:
причем плоскости не параллельны и не совпадают, т.е. хотя бы одно из равенств в соотношении И ФУНКЦИИ Примеры. 1. 2. Определение 4.2. Последовательность называется ограниченной, если существует число М, такое, что Последовательность называется ограниченной сверху (снизу), если существует число М, такое, что Определение 4.3. Число а называется пределом числовой последовательности " e > 0 $ N " n > N | хn - а | < e. В этом случае пишут Если последовательность Определение 4.4. Интервал
Интервал (a - e, a + e) также будет окрестностью точки а. Он называется e- окрестностью точки а. При этом неравенство | хn - а | < e может быть переписано в виде: Понятие предела является базовым понятием математического анализа. Сформулируем определение предела последовательности по-другому. Определение 4.5. Число а называется пределом числовой последовательности
Рис. 4.1
Отметим, что номер N в определении предела, вообще говоря, зависит от ε. Чем меньшую e-окрестность приходится рассматривать, тем более удаленные точки последовательности приходится брать. 6. Свойства предела последовательности Элементарные свойства предела последовательности: 1. Если последовательность имеет предел, то он единственен. 2. Если последовательность сходится, то она ограничена. 3 (о предельном переходе в неравенствах). Если последовательности 4. Если Арифметические свойства пределов последовательностей: Пусть 1. 2. 3. Заметим, что пределы суммы, разности, произведения и частного могут существовать и без существования пределов 7. Бесконечно малые и бесконечно большие величины Определение 4.6. Последовательность Обозначение: Последовательность Обозначение: Бесконечно большая величина ни к какому конечному пределу не стремится. Если бесконечно большая величина Теорема 4.1. Для того, чтобы последовательность Свойства бесконечно малых последовательностей: 1. Последовательность 2. Стационарная последовательность 3. Если отбросить (или добавить) конечное число членов бесконечно малой последовательности, то она останется бесконечно малой последовательностью. 4. Если 5. Бесконечно малая последовательность является ограниченной. 6. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность. 7. Если 8. Если 9. Если Можно определить понятие предела последовательности на языке бесконечно малых последовательностей: число а называется пределом последовательности 8. Монотонная ограниченная последовательность Определение 4.7. Последовательность Последовательность Все такие последовательности называются монотонными. При этом говорят, что последовательность монотонно возрастает или монотонно убывает. Теорема 4.2. Пусть Рассмотрим числовую последовательность
Это число имеет исключительную важность для математического анализа и его приложений. Некоторые свойства числа е делают особо выгодным выбор этого числа в качестве основания логарифма. Такие логарифмы называются натуральными и обозначаются ln. 9. Критерий Коши существования предела последовательности Критерий Коши является общим признаком существования предела последовательности. Он позволяет определять сходимость последовательности без нахождения самого предела последовательности. Определение 4.8. Последовательность Фундаментальную последовательность можно еще определить следующим образом: " e > 0 $ N " n > N, " p Î N| Теорема 4.3. (Критерий Коши). Чтобы последовательность Примеры. 1).
2).
Предел функции 10. Предел функции на бесконечности Понятие предела функции на бесконечности является в определенном смысле обобщением понятия предела последовательности. Определение 4.9. Функцию f (x) определённую на луче (Q, +¥), называют бесконечно малой при х ® +¥, если " e > 0 $ М > 0 такое, что " x > M выполняется | f (x)| < e. См. рис. 4.2. Обозначение: Функцию f (x), определенную на луче (– ¥, а) называют бесконечно малой при х ® – ¥, если " e > 0 $ M > 0 такое, что " x < - M выполняется| f (x)| < e. Обозначение: Поскольку вместо двух неравенств х <- М, x > M можно записать | х | > М, то можно объединить два приведенных выше определения в одно. Функцию, определённую на (– ¥; a 1) È(a 2; + ¥), называют бесконечно малой при х ® ¥ (±¥), если " e > 0 $ M > 0 такое, что " x, если | x |> M,то | f (x)| < e. Обозначение:
Рис. 4.2 Рис. 4.3
Определение 4.10. Число b называют пределом функции f(x) при х®¥, если | f (x) – b | – бесконечно малая функция при х ® ¥, при этом пишут Приведем определение предела функции на бесконечности по Коши. Определение 4.11. Число b называют пределом функции f(x) при х ® ¥, если " e > 0 $ M > 0 " x;если | x | > M,то| f (x) - b | < e. См. рис. 4.3. 11. Предел функции в точке Определение 4.12. Функцию f (x)называют бесконечно малой при х ® а, если " e > 0 $ d> 0 " x из неравенства| x – a |<dследует неравенство | f (x) | < e. См. рис. 4.4. Обозначение:
Рис. 4.4 Рис. 4.5
Число b называют пределом функции f(x) при х ® а, если f (х) – b является бесконечно малой функцией при х ® а. При этом пишут Можно снова привести определение предела функции в точке по Коши или, другими словами, на языке e-d. Определение 4.13. Число b называют пределом функции f (x) при х ® а, если " e > 0 $ d> 0 " x, если | x – a |<d, то | f (x) – b | < e. Определение предела говорит о том, что если х приближается к а по любому закону, оставаясь не равным а, то f (x) приближается к b, делается как угодно близким к b. 12. Бесконечно большие функции Определение 4.14. Функция у = f (х), определённая на объединении двух лучей (–¥; a 1) È(a 2; +¥), называется бесконечно большой при х ® ¥, если " P > 0 $ M > 0 " x, если | x |> M, то| f (x)| > Р. Обозначение: Можно так же определить бесконечно большую функцию в точке. Определение 4.15. Функцию f (x)называют бесконечно большой при х ® а, если " Р > 0 $ d> 0 " x из неравенства| x – a |<dследует неравенство | f (x) | > P. См. рис. 4.5. Обозначение: Приведем свойства бесконечно малых и бесконечно больших функций. При этом будем предполагать, что а – либо конечное число, либо 1. Если 2. Постоянная функция у = с является бесконечно малой при х ® а тогда и только тогда, когда c = 0. 3. Сумма, произведение конечного числа бесконечно малых функций является бесконечно малой функцией. 4. Если f (x) – бесконечно малая функция при х ® а, то она является ограниченной в некоторой окрестности точки а. 5. Если f (x) – бесконечно малая функция при х ® а, а g (x) – ограниченная функция в некоторой окрестности точки а, то их произведение 6. Если f (х) – бесконечно малая функция при х ® а и в некоторой окрестности точки а выполняется неравенство | g (x)| £ | f (х)|, то и g (x) – есть бесконечно малая функция на соответствующем интервале. 7. Если 8. Если 13. Свойства предела функции Снова будем предполагать, что а – либо конечное число, либо 1. Если функция имеет предел при х ® а, то он единственен. 2. Если функция имеет конечный предел при х ® а, то она ограничена в некоторой окрестности точки а. 3. О предельном переходе в неравенствах. Если |
|||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 317; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.5.176 (0.016 с.) |

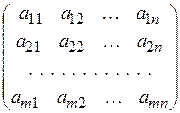 или, сокращенно А = (
или, сокращенно А = ( ),
), .
. , у которой каждая строка является столбцом матрицы А с тем же номером (и, следовательно, каждый столбец является строкой матрицы А), называется транспонированной к матрице А. Переход от матрицы А к В называется транспонированием. Будем обозначать транспонированную матрицу АТ.
, у которой каждая строка является столбцом матрицы А с тем же номером (и, следовательно, каждый столбец является строкой матрицы А), называется транспонированной к матрице А. Переход от матрицы А к В называется транспонированием. Будем обозначать транспонированную матрицу АТ. .
. и
и 
 для i= 1, 2,…, n, j = 1, 2, …, m. Равенство матриц обозначается А = В.
для i= 1, 2,…, n, j = 1, 2, …, m. Равенство матриц обозначается А = В.
 для i = 1, 2, …, n, j = 1, 2, …, m.
для i = 1, 2, …, n, j = 1, 2, …, m. , где i = 1, 2, …, n, j = 1, 2, …, m.
, где i = 1, 2, …, n, j = 1, 2, …, m. , если
, если (1.1)
(1.1)
 .
. ;
; .
. .
. (2.1)
(2.1) (2.2)
(2.2) .
. .
.
 элемента
элемента  . (2.3)
. (2.3) (2.4)
(2.4) (2.5)
(2.5) (2.6)
(2.6) .
. .
. .
. .
. ,
, к элементу
к элементу  стоит на месте (ji), т.е. на пересечении j- й строки и i- го столбца.
стоит на месте (ji), т.е. на пересечении j- й строки и i- го столбца.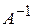 называется обратной к матрице А, если выполняется условие
называется обратной к матрице А, если выполняется условие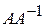 =
=  = Е,
= Е, делением всех ее элементов на det A:
делением всех ее элементов на det A: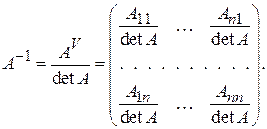 (3.1)
(3.1) , причем det А ≠ 0.
, причем det А ≠ 0.
 :
: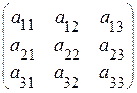 ∙
∙  =
= =
= = det A ∙
= det A ∙  = det A ∙ E,
= det A ∙ E, и
и  .
. , т.е.
, т.е. 
 ;
; ;
; .
. .
.
 ,
,  называются коэффициентами системы, числа
называются коэффициентами системы, числа  - свободными членами.
- свободными членами. .
. .
. системы, дополненная столбцом свободных членов
системы, дополненная столбцом свободных членов .
. называется решением системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел
называется решением системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел  .
.
 (3.28)
(3.28) не должно выполняться.
не должно выполняться.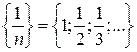 .
. .
. .
.
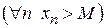 .
. , если для любого e > 0 найдётся натуральное число N такое, что для " п > N выполняется неравенство | хn - а | < e. Или, используя краткую запись,
, если для любого e > 0 найдётся натуральное число N такое, что для " п > N выполняется неравенство | хn - а | < e. Или, используя краткую запись, или хn ® а и говорят, что хn стремится к а или последовательность
или хn ® а и говорят, что хn стремится к а или последовательность  , содержащий в себе точку а, называется окрестностью точки а.
, содержащий в себе точку а, называется окрестностью точки а. (a - e, a + e).
(a - e, a + e).
 сходятся и
сходятся и 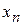 £
£  для всех n, то
для всех n, то  .
.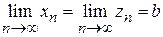 и для всех п справедливо неравенство
и для всех п справедливо неравенство 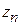 , то
, то  .
. и
и  .
. .
.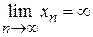 .
.
 . Однако существуют бесконечно большие, для которых
. Однако существуют бесконечно большие, для которых  и
и  .
. , где
, где  – бесконечно малая величина.
– бесконечно малая величина. является бесконечно малой тогда и только тогда, когда с = 0.
является бесконечно малой тогда и только тогда, когда с = 0. – бесконечно малая.
– бесконечно малая. .
. (
( ).
). (
( ).
). .
. »2,718281…(4.1)
»2,718281…(4.1) | < e.
| < e. -
- 


 т. к.
т. к. 
 .
. .
.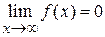 .
.

 .
. .
.

 .
. .
. .
. (+∞ или –∞).
(+∞ или –∞). , где
, где  – бесконечно малая при
– бесконечно малая при  . Верно и обратное.
. Верно и обратное.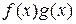 является бесконечно малой функцией при
является бесконечно малой функцией при  – бесконечно малая при
– бесконечно малая при  , то
, то  – бесконечно большая, т.е.
– бесконечно большая, т.е.  .
.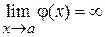 , то
, то  .
. и в некоторой окрестности точки а выполняется неравенство f (х) £ g (x), то b
и в некоторой окрестности точки а выполняется неравенство f (х) £ g (x), то b