
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции, непрерывные на отрезкеСодержание книги
Поиск на нашем сайте
Определение 4.25. Функция называется непрерывной на отрезке, если она непрерывна в каждой точке этого отрезка. Функция f: Е ® R называется непрерывной, если она непрерывна в каждой точке своей области определения Е. Перечислим свойства функций, непрерывных на отрезке. 1). Пусть функция 2). Пусть функция
Рис. 4.9 Рис. 4.10
3). Пусть функция
Рис. 4.11 Рис. 4.12 4). Пусть функция Заметим, в свойствах 1 и 2 существенно, что
Контрольные вопросы 1. Числовая последовательность и ее предел. 2. Свойства предела числовой последовательности. 3. Бесконечно малые и бесконечно большие величины. 4. Свойства бесконечно малых последовательностей. 5. Монотонная ограниченная последовательность. 6. Критерий Коши существования предела последовательности. 7. Предел функции на бесконечности. 8. Предел функции в точке. 9. Бесконечно большие функции. 10. Свойства предела функции. 11. Односторонние пределы. 12. Критерий Коши существования предела функции. 13. Замечательные пределы. 14. Виды неопределенностей. 15. Сравнение бесконечно малых функций. 16. Таблица эквивалентных бесконечно малых функций. Применение эквивалентных бесконечно малых при вычислении пределов. 17. Непрерывность функции в точке. 18. Необходимое и достаточное условие непрерывности функции в точке. 19. Функции, непрерывные на отрезке.
ЛЕКЦИЯ № 5. ПРОИЗВОДНАЯ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ Определение производной функции. Ее геометрический И физический смысл
Понятие производной возникло в результате усилий, направленных на решение таких задач, как задача о проведении касательной к кривой или задача о вычислении скорости неравномерного движения.
1. Рассмотрим вопрос о нахождении касательной к графику функции y = f (x) в точке М (х, у) предполагая, что касательная существует. Пусть М′ (х + D х, у + D у) – произвольная точка на кривой у = f (х). Пусть секущая ММ' составляет с положительным направлением оси ОХ угол j. Из прямоугольного треугольника MM’N (см. рис. 5.1) находим tg j =
Рис. 5.1
Пусть М' ® М, тогда D х ® 0 и секущая стремится к своему предельному положению – касательной МТ в точке М. Обозначим через a угол между касательной МТ и направлением оси ОХ. Тогда при D х ® 0 имеем j ® a и в силу непрерывности тангенса tg j® tg a. Таким образом, угловой коэффициент касательной в точке М будет равен
Итак, угловой коэффициент касательной к графику функции у = f(x) в точке х равен значению ее производной в этой точке: k = f '(х). 2. Пусть уравнение х = f (t), где f – функция от времени t, а х – пройденный путь, выражает закон движения материальной точки. Необходимо найти скорость движущей точки. Пусть в некоторый момент времени t точка занимает положение М (ОМ = х). В момент t + D t точка займет положение М' (OМ' = х + D х) (см. рис. 5.2).
Рис. 5.2
Отсюда х + D х = f (t + D t). За время D t точка пройдет путь D x = f (t + D t) – f (t). Следовательно, отношение Обе задачи привели к одной и той же математической операции, которую назвали дифференцированием функции, а результат – производной функции. Определение 5.1. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
Теорема 5.1. Если функция имеет производную в точке, то она является непрерывной в этой точке. Обратное утверждение неверно: непрерывная в точке функция может не иметь производной в этой точке. Примером такой функции является у = | х |. Эта функция непрерывна в точке х = 0, но не имеет производной в этой точке, так как в этой точке не существует касательной к графику функции у = | х |.
Дифференциал функции Для функции y = f (x) рассмотрим производную
Определение 5.2. Функция называется дифференцируемой в точке х, если ее приращение Величина А ∆ x называется дифференциалом функции f (x) и обозначается dy = А∆x = f′ (x) ∆ x. Величина
Теорема 5.2. Функция f (x) дифференцируема в точке х тогда и только тогда, когда она имеет производную в этой точке, равную А. Заметим, что мы можем рассматривать производную, как отношение двух дифференциалов:
Операция нахождения производной функции называется дифференцированием функции.
Правила дифференцирования. Свойства дифференциала. Таблица производных 1) Производная константы равна нулю, т.е. 2) Если функция f (х) имеет производную в точке х, то С∙f (х) также имеет производную в точке х, и при этом
3) Если функции и (х) и v (x) имеют производные в точке х, то их сумма f (х) = и (х) + v (x) также имеет производную в точке х, и при этом
4) Если функции и (х) и v (x) имеют производные в точке х, то их произведение f (x) = u (x)× v (x) также имеет производную в точке х и
5) Если функции и (х) и v (x) имеют производные в точке х и, кроме того, v (x)¹ 0, то частное
6) Пусть дана сложная функция у = f (u), где и = g (x) и пусть u = g (x)имеет производную в точке х, а функция y = f (u) имеет производную в точке и = g (x). Тогда сложная функция у = f (g (х)) имеет производную в точке х и
5. Свойства дифференциала dc = 0, c = const. d (u ± v) = du ± dv. d (cu) = c du, c = const. d (uv) = v du + u×dv.
Дифференциал сложной функции: если y = f (x), x = φ(t), то Инвариантность формы первого дифференциала относительно выбора переменных: дифференциал функции равен произведению производной этой функции на дифференциал аргумента, при этом безразлично, будет ли этот аргумент независимой переменной или функцией от другой независимой переменной. Таким образом, если
6. Таблица производных основных элементарных функций (таб. 5.1) 7. Таблица 5.1
Примеры.
2.
3.
|
||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 395; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.138.124 (0.01 с.) |

 непрерывна на
непрерывна на  , тогда
, тогда  ограничена на
ограничена на  (см. рис. 4.9).
(см. рис. 4.9). и наименьшее
и наименьшее  значения на
значения на 
 и
и 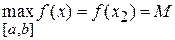 (см. рис. 4.10).
(см. рис. 4.10).

 (см. рис. 4.11).
(см. рис. 4.11).

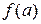 ,
,  имеют разные знаки, тогда существует, по крайней мере, одна точка
имеют разные знаки, тогда существует, по крайней мере, одна точка  , такая что
, такая что  (см. рис. 4.12).
(см. рис. 4.12). непрерывна на отрезке, а не на интервале. Например,
непрерывна на отрезке, а не на интервале. Например,  непрерывна на
непрерывна на  , но она не ограничена на этом интервале. Далее,
, но она не ограничена на этом интервале. Далее,  непрерывна на
непрерывна на  , но она не достигает максимума и минимума на этом интервале.
, но она не достигает максимума и минимума на этом интервале.

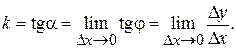 Мы пришли к понятию производной функции в точке х:
Мы пришли к понятию производной функции в точке х:

 выражает скорость движения точки за промежуток времени D t. Предел этого отношения при D t ® 0 есть мгновенная скорость, т.е. скорость движения в момент времени t:
выражает скорость движения точки за промежуток времени D t. Предел этого отношения при D t ® 0 есть мгновенная скорость, т.е. скорость движения в момент времени t: 
 (5.1)
(5.1) Отсюда, по определению предела, величина
Отсюда, по определению предела, величина 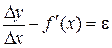 является бесконечно малой. Тогда
является бесконечно малой. Тогда  или
или  , где А = f ′(x) – константа. Таким образом, приращение ∆ y отличается от величины
, где А = f ′(x) – константа. Таким образом, приращение ∆ y отличается от величины  на бесконечно малую величину
на бесконечно малую величину  более высокого порядка, чем ∆ x.
более высокого порядка, чем ∆ x. в этой точке можно записать в виде:
в этой точке можно записать в виде:  называется дифференциалом независимой переменной и обозначается
называется дифференциалом независимой переменной и обозначается  . Тогда
. Тогда (5.2)
(5.2) (5.3)
(5.3) .
. (5.4)
(5.4) (5.5)
(5.5)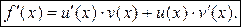 (5.6)
(5.6) также имеет производную в точке x и
также имеет производную в точке x и (5.7)
(5.7) (5.8)
(5.8) .
. .
.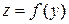 и
и  , то
, то  . Тогда свойство инвариантности выражается формулой:
. Тогда свойство инвариантности выражается формулой: (5.9)
(5.9)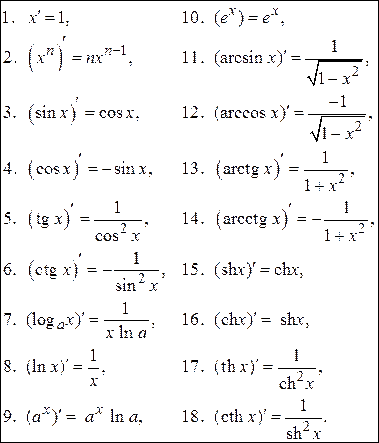

 . Воспользуемся правилом дифференцирования произведения функций:
. Воспользуемся правилом дифференцирования произведения функций:
 . Воспользуемся правилом дифференцирования частного функций:
. Воспользуемся правилом дифференцирования частного функций: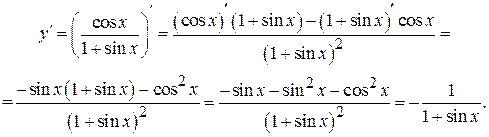
 .Так как эта функция сложная, то воспользуемся правилом дифференцирования сложной функции:
.Так как эта функция сложная, то воспользуемся правилом дифференцирования сложной функции:



