
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неполные уравнения плоскости.Содержание книги
Поиск на нашем сайте
Общее уравнение плоскости (3.20) называется полным, если все коэффициенты А, В, С и D отличны от нуля. В противном случае уравнение плоскости называется неполным. Рассмотрим различные виды неполных уравнений плоскости: 1) D = 0, уравнение Ах + Ву + Cz = 0 определяет плоскость, проходящую через начало координат; 2) А = 0, уравнение Ву + Сz + D = 0 определяет плоскость, параллельную оси Ох; 3) В = 0, уравнение Ах + Сz + D = 0 определяет плоскость, параллельную оси Оу; 4) С = 0, уравнение Ах + Ву + D = 0 определяет плоскость, параллельную оси Оz; 5) A = 0, B = 0, уравнение Cz + D = 0 определяет плоскость, параллельную координатной плоскости Оху; 6) A = 0, С = 0, уравнение Ву + D = 0 определяет плоскость, параллельную координатной плоскости Охz; 7) B = 0, C = 0, уравнение Ax + D = 0 определяет плоскость, параллельную координатной плоскости Оуz; 8) A = 0, B = 0, D = 0, уравнение Cz = 0 равносильно уравнению z = 0 и определяет координатную плоскость Оху; 9) A = 0, С = 0, D = 0, уравнение Ву = 0 равносильно уравнению у = 0 и определяет координатную плоскость Охz; 10) B = 0, C = 0, D = 0, уравнение Ax = 0 равносильно уравнению x = 0 и определяет координатную плоскость Оуz. Уравнение плоскости в отрезках.
Заметим, что числа a, b и c имеют простой геометрический смысл: они равны алгебраическим величинам отрезков, которые плоскость отсекает на координатных осях Ох, Оу и Оz, соответственно (см. рис. 3.5).
Рис. 3.5
Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой. Пусть Уравнение плоскости, проходящей через три точки, имеет вид
Пример. Записать уравнение плоскости, проходящей через три точки Решение. Воспользуемся формулой (3.22):
Раскрывая определитель, получим искомое уравнение плоскости: Уравнение плоскости, параллельной данному вектору и проходящей через две данные точки Пусть дан вектор а = (т, п, l) и две различные точки
Уравнение плоскости, параллельной двум неколлинеарным векторам и проходящей через точку.
Пусть даны два вектора а Уравнение плоскости, параллельной векторам а
7. Уравнение плоскости, проходящей через точку
|
|||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.210.20 (0.007 с.) |

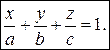 (3.21)
(3.21)
 ,
,  и
и  – три различные точки, не лежащие на одной прямой. Известно, что через три точки всегда можно провести плоскость, и она будет единственной, если точки не лежат на одной прямой.
– три различные точки, не лежащие на одной прямой. Известно, что через три точки всегда можно провести плоскость, и она будет единственной, если точки не лежат на одной прямой. (3.22)
(3.22)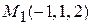 ,
,  и
и 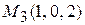 .
. .
.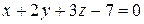 .
. (3.23)
(3.23) и а
и а  и точка
и точка  и а
и а  не коллинеарны, то через точку
не коллинеарны, то через точку  можно провести единственную плоскость, параллельную векторам а
можно провести единственную плоскость, параллельную векторам а  (3.24)
(3.24) перпендикулярно вектору п (А, В, С):
перпендикулярно вектору п (А, В, С): (3.25)
(3.25)


