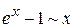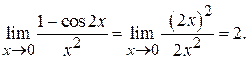Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция № 4. Предел числовой последовательностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
И ФУНКЦИИ Предел числовой последовательности
Определение 4.1. Пусть каждому натуральному числу Числа Примеры. 1. 2. Определение 4.2. Последовательность называется ограниченной, если существует число М, такое, что Последовательность называется ограниченной сверху (снизу), если существует число М, такое, что Определение 4.3. Число а называется пределом числовой последовательности " e > 0 $ N " n > N | хn - а | < e. В этом случае пишут Если последовательность Определение 4.4. Интервал Интервал (a - e, a + e) также будет окрестностью точки а. Он называется e- окрестностью точки а. При этом неравенство | хn - а | < e может быть переписано в виде: Понятие предела является базовым понятием математического анализа. Сформулируем определение предела последовательности по-другому. Определение 4.5. Число а называется пределом числовой последовательности
Рис. 4.1
Отметим, что номер N в определении предела, вообще говоря, зависит от ε. Чем меньшую e-окрестность приходится рассматривать, тем более удаленные точки последовательности приходится брать. 6. Свойства предела последовательности Элементарные свойства предела последовательности: 1. Если последовательность имеет предел, то он единственен. 2. Если последовательность сходится, то она ограничена. 3 (о предельном переходе в неравенствах). Если последовательности 4. Если Арифметические свойства пределов последовательностей: Пусть 1. 2. 3. Заметим, что пределы суммы, разности, произведения и частного могут существовать и без существования пределов 7. Бесконечно малые и бесконечно большие величины Определение 4.6. Последовательность Обозначение: Последовательность Обозначение: Бесконечно большая величина ни к какому конечному пределу не стремится. Если бесконечно большая величина Теорема 4.1. Для того, чтобы последовательность Свойства бесконечно малых последовательностей: 1. Последовательность 2. Стационарная последовательность 3. Если отбросить (или добавить) конечное число членов бесконечно малой последовательности, то она останется бесконечно малой последовательностью. 4. Если 5. Бесконечно малая последовательность является ограниченной. 6. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность. 7. Если 8. Если 9. Если Можно определить понятие предела последовательности на языке бесконечно малых последовательностей: число а называется пределом последовательности 8. Монотонная ограниченная последовательность Определение 4.7. Последовательность Последовательность Все такие последовательности называются монотонными. При этом говорят, что последовательность монотонно возрастает или монотонно убывает. Теорема 4.2. Пусть Рассмотрим числовую последовательность
Это число имеет исключительную важность для математического анализа и его приложений. Некоторые свойства числа е делают особо выгодным выбор этого числа в качестве основания логарифма. Такие логарифмы называются натуральными и обозначаются ln. 9. Критерий Коши существования предела последовательности Критерий Коши является общим признаком существования предела последовательности. Он позволяет определять сходимость последовательности без нахождения самого предела последовательности. Определение 4.8. Последовательность Фундаментальную последовательность можно еще определить следующим образом: " e > 0 $ N " n > N, " p Î N| Теорема 4.3. (Критерий Коши). Чтобы последовательность Примеры. 1).
2).
Предел функции 10. Предел функции на бесконечности Понятие предела функции на бесконечности является в определенном смысле обобщением понятия предела последовательности. Определение 4.9. Функцию f (x) определённую на луче (Q, +¥), называют бесконечно малой при х ® +¥, если " e > 0 $ М > 0 такое, что " x > M выполняется | f (x)| < e. См. рис. 4.2. Обозначение: Функцию f (x), определенную на луче (– ¥, а) называют бесконечно малой при х ® – ¥, если " e > 0 $ M > 0 такое, что " x < - M выполняется| f (x)| < e. Обозначение: Поскольку вместо двух неравенств х <- М, x > M можно записать | х | > М, то можно объединить два приведенных выше определения в одно. Функцию, определённую на (– ¥; a 1) È(a 2; + ¥), называют бесконечно малой при х ® ¥ (±¥), если " e > 0 $ M > 0 такое, что " x, если | x |> M,то | f (x)| < e. Обозначение:
Рис. 4.2 Рис. 4.3
Определение 4.10. Число b называют пределом функции f(x) при х®¥, если | f (x) – b | – бесконечно малая функция при х ® ¥, при этом пишут Приведем определение предела функции на бесконечности по Коши. Определение 4.11. Число b называют пределом функции f(x) при х ® ¥, если " e > 0 $ M > 0 " x;если | x | > M,то| f (x) - b | < e. См. рис. 4.3. 11. Предел функции в точке Определение 4.12. Функцию f (x)называют бесконечно малой при х ® а, если " e > 0 $ d> 0 " x из неравенства| x – a |<dследует неравенство | f (x) | < e. См. рис. 4.4. Обозначение:
Рис. 4.4 Рис. 4.5
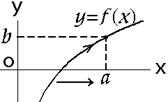
Число b называют пределом функции f(x) при х ® а, если f (х) – b является бесконечно малой функцией при х ® а. При этом пишут Можно снова привести определение предела функции в точке по Коши или, другими словами, на языке e-d. Определение 4.13. Число b называют пределом функции f (x) при х ® а, если " e > 0 $ d> 0 " x, если | x – a |<d, то | f (x) – b | < e. Определение предела говорит о том, что если х приближается к а по любому закону, оставаясь не равным а, то f (x) приближается к b, делается как угодно близким к b. 12. Бесконечно большие функции Определение 4.14. Функция у = f (х), определённая на объединении двух лучей (–¥; a 1) È(a 2; +¥), называется бесконечно большой при х ® ¥, если " P > 0 $ M > 0 " x, если | x |> M, то| f (x)| > Р. Обозначение: Можно так же определить бесконечно большую функцию в точке. Определение 4.15. Функцию f (x)называют бесконечно большой при х ® а, если " Р > 0 $ d> 0 " x из неравенства| x – a |<dследует неравенство | f (x) | > P. См. рис. 4.5. Обозначение: Приведем свойства бесконечно малых и бесконечно больших функций. При этом будем предполагать, что а – либо конечное число, либо 1. Если 2. Постоянная функция у = с является бесконечно малой при х ® а тогда и только тогда, когда c = 0. 3. Сумма, произведение конечного числа бесконечно малых функций является бесконечно малой функцией. 4. Если f (x) – бесконечно малая функция при х ® а, то она является ограниченной в некоторой окрестности точки а. 5. Если f (x) – бесконечно малая функция при х ® а, а g (x) – ограниченная функция в некоторой окрестности точки а, то их произведение 6. Если f (х) – бесконечно малая функция при х ® а и в некоторой окрестности точки а выполняется неравенство | g (x)| £ | f (х)|, то и g (x) – есть бесконечно малая функция на соответствующем интервале. 7. Если 8. Если 13. Свойства предела функции Снова будем предполагать, что а – либо конечное число, либо 1. Если функция имеет предел при х ® а, то он единственен. 2. Если функция имеет конечный предел при х ® а, то она ограничена в некоторой окрестности точки а. 3. О предельном переходе в неравенствах. Если 4. О пределе промежуточной функции. Если 5. Арифметические свойства пределов: пусть а) б) в) 14. Односторонние пределы Определение 4.16. Число b называется левым пределом функции f (x) при х ® а, если " e > 0 $ d> 0 " x: 0 < a – x <d Þ | f (x) – b | < e. См. рис. 4.6. Обозначение: Число b называется правым пределом функции f (x) при х ® а, если " e > 0 $ d> 0 " x: 0 < x – a <d Þ | f (x) – b | < e. См. рис. 4.7. Обозначение: Если а = 0, то используют обозначение
Рис. 4.6 Рис. 4.7
Можно дать другие определения левого и правого пределов. Определение 4.17. Левой окрестностью точки а называется произвольный полуинтервал Левая и правая окрестности точки ∞ будут, соответственно, Определение 4.18. Число b называется левым (правым) пределом функции f (x) при х ® а, если Левый и правый пределы в точке ∞ записываются следующим образом: Левый и правый пределы называют односторонними, обычный предел называют двусторонним. Теорема 4.4. Для того чтобы существовал
15. Критерий Коши существования предела функции Так же как и для последовательности, для функции существует аналогичный критерий Коши существования предела. Определение 4.19. Функция Теорема 4.5 (Критерий Коши). Для того чтобы функция 16. Замечательные пределы Первый замечательный предел: Эта формула получается из неравенства: Второй замечательный предел записывается в двух видах:
Существование этого предела для натуральных х было обосновано при изучении числовых последовательностей. Примеры. 1. 2.
17. Виды неопределенностей При вычислении пределов могут возникнуть так называемые неопределенности. Например, предел отношения Перечислим все неопределенности, которые могут возникнуть при вычислении пределов: При возникновении неопределенности в каждом конкретном примере необходимо преобразовать выражение под знаком предела так, чтобы неопределенность исчезла. От неопределенности вида 18. Сравнение бесконечно малых Определение 4.20. Две бесконечно малые
Определение 4.21. Бесконечно малая Порядок бесконечно малой функции можно определить из условия: если Например,
Теорема 4.6. Пусть
где Для применения этой теоремы на практике полезно знать как можно больше пар эквивалентных функций. Приведем наиболее часто используемые эквивалентности (при Таблица 4.1.
Примеры. 1). Воспользовались эквивалентностью
Непрерывность функции
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1654; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.70.138 (0.009 с.) |

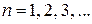 приведено в соответствие число
приведено в соответствие число  . Тогда говорят, что задана числовая последовательность
. Тогда говорят, что задана числовая последовательность 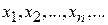 и обозначают ее
и обозначают ее  .
. называются элементами последовательности, а выражение
называются элементами последовательности, а выражение 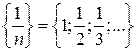 .
. .
. .
.
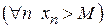 .
. или хn ® а и говорят, что хn стремится к а или последовательность
или хn ® а и говорят, что хn стремится к а или последовательность  , содержащий в себе точку а, называется окрестностью точки а.
, содержащий в себе точку а, называется окрестностью точки а. (a - e, a + e).
(a - e, a + e).
 сходятся и
сходятся и 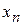 £
£  для всех n, то
для всех n, то  .
.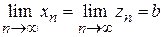 и для всех п справедливо неравенство
и для всех п справедливо неравенство 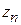 , то
, то  .
. .
. .
.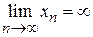 .
.
 . Однако существуют бесконечно большие, для которых
. Однако существуют бесконечно большие, для которых  и
и  .
. , где
, где  – бесконечно малая величина.
– бесконечно малая величина. является бесконечно малой тогда и только тогда, когда с = 0.
является бесконечно малой тогда и только тогда, когда с = 0. – бесконечно малая.
– бесконечно малая. .
. (
( ).
). (
( ).
). .
. »2,718281…(4.1)
»2,718281…(4.1) | < e.
| < e. -
- 


 т. к.
т. к. 
 .
. .
.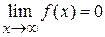 .
.

 .
. .
.

 .
. .
. .
. (+∞ или –∞).
(+∞ или –∞). , где
, где  – бесконечно малая при
– бесконечно малая при  . Верно и обратное.
. Верно и обратное.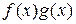 является бесконечно малой функцией при
является бесконечно малой функцией при  – бесконечно малая при
– бесконечно малая при  , то
, то  – бесконечно большая, т.е.
– бесконечно большая, т.е.  .
.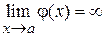 , то
, то  .
. и в некоторой окрестности точки а выполняется неравенство f (х) £ g (x), то b £ c.
и в некоторой окрестности точки а выполняется неравенство f (х) £ g (x), то b £ c. и в некоторой окрестности точки а справедливо f (x) £ g (x) £ h (x), то
и в некоторой окрестности точки а справедливо f (x) £ g (x) £ h (x), то  .
. ,
, ,
, , если c ¹ 0.
, если c ¹ 0. .
. .
. и
и  .
.

 , а правой окрестностью точки а называется произвольный полуинтервал
, а правой окрестностью точки а называется произвольный полуинтервал  .
. и
и  .
. определена в некоторой левой (правой) окрестности точки а, и если " e > 0 $ левая (правая) окрестность
определена в некоторой левой (правой) окрестности точки а, и если " e > 0 $ левая (правая) окрестность  , такая что
, такая что 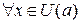 ,
, 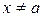 , выполняется | f (x) – b | < e.
, выполняется | f (x) – b | < e. и
и 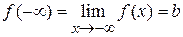 .
. , необходимо и достаточно, чтобы существовали односторонние пределы
, необходимо и достаточно, чтобы существовали односторонние пределы  и
и  и чтобы они были равны между собой, т.е.
и чтобы они были равны между собой, т.е. .
. окрестность
окрестность  справедливо
справедливо  , или на языке
, или на языке  :
: 
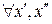 , если
, если  , то
, то  (4.2)
(4.2) , которое верно в некоторой окрестности нуля. Положим сначала, что х положительно, тогда
, которое верно в некоторой окрестности нуля. Положим сначала, что х положительно, тогда 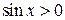 и поэтому
и поэтому  . Переворачивая неравенство, получаем
. Переворачивая неравенство, получаем  . Отметим, что последнее неравенство верно и при х отрицательных, так как
. Отметим, что последнее неравенство верно и при х отрицательных, так как  и
и  . Поскольку
. Поскольку  , то по свойству о пределе промежуточной функции получаем:
, то по свойству о пределе промежуточной функции получаем: 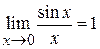 .
.
 (4.3)
(4.3) .
.
 при условии
при условии  и
и  может принимать различные значения, в том числе равняться бесконечности, или даже не существовать. В этом случае говорят, что имеется неопределенность вида
может принимать различные значения, в том числе равняться бесконечности, или даже не существовать. В этом случае говорят, что имеется неопределенность вида  .
. ,
,  ,
,  ,
,  ,
,  ,
, 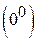 .
. называются величинами одного и того же порядка малости при
называются величинами одного и того же порядка малости при  В частности, если k = 1, то говорят, что
В частности, если k = 1, то говорят, что  .
.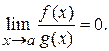
 , то
, то  – бесконечно малая порядка 1 при
– бесконечно малая порядка 1 при  , а
, а 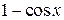 – бесконечно малая порядка 2, так как
– бесконечно малая порядка 2, так как ,
,  .
. ~
~  при
при 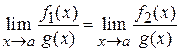 ,
,  ,
, ,
,