
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление первого и второго замечательных пределовСодержание книги
Поиск на нашем сайте МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ для выполнения практических работ по дисциплине «Математика»
Для специальностей: 42.02.01 Реклама
Пермь 2014 Методические рекомендации для выполнения практических работ по дисциплине «Математика» предназначены для студентов специальности 42.02.01 «Реклама».
Рассмотрено на заседании ЦМК преподавателей общеобразовательных дисциплин Председатель ЦМК Дозморов В.А.
Утверждено научно-методическим советом ПТПТД Зам. директора по НМР Рогова М.Н.
Составитель:Калинина Наталья Сергеевна, преподаватель математики КГАПОУ Пермского техникума профессиональных технологий и дизайна ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Методические рекомендации на выполнение практических работ по дисциплине «Математика» предназначены для обучающихся по основной профессиональной образовательной программе 42.02.01 «Реклама». Практические работы направлены на экспериментальное подтверждение теоретических положений и формирование учебных, профессиональных практических умений, общих и профессиональных компетенций обучающихся и составляют важную часть их профессиональной подготовки. Практические занятия способствуют интеграции мыслительной и практической деятельности обучающихся, развитию коммуникативных способностей, профессиональной самостоятельности и мобильности. В процессе практического занятия обучающиеся выполняют практическую работу под руководством преподавателя в соответствии с изучаемым содержанием учебного материала рабочих учебных программ по дисциплине. Данные методические рекомендации ориентированы на то, что в учебном процессе практические занятия являются основными видами учебных занятий, а практические работы выступают в качестве предметно-содержательной составляющей учебного занятия. Целями проведения практических занятий являются: обобщение, систематизацию, углубление, закрепление полученных теоретических знаний по конкретным темам дисциплины «Математика»; формирование умений применять полученные знания на практике, реализацию единства интеллектуальной и практической деятельности; выработку при решении поставленных задач таких профессионально значимых качеств, как самостоятельность, ответственность, точность, творческая инициатива. Каждая практическая работа состоит их двух частей: задания для подготовки к работе и задания для ее выполнения. Поэтому перед занятием студент должен повторить пройденный материал, используя конспекты лекций, и рекомендуемую литературу, указанную в задании к каждой работе, а также ознакомиться с основными сведениями, приведенными в данной работе. Практические работы выполняются обучающимися индивидуально. Отчет по каждой работе составляется каждым обучающимся самостоятельно. Отчет должен быть составлен по следующей примерной форме: - дата; - наименование темы; - цель работы; - ответы на вопросы для подготовки к работе; - содержание работы;
Практическая работа № 1 Раскрытие неопределенности вида Время проведения – 2 часа. Цель работы: научиться вычислять пределы функций путем раскрытия неопределенностей вида Вопросы для подготовки к работе: 1. Понятие предела последовательности; 2. Понятие предела функции; 3. Бесконечно малые и бесконечно большие, связь между ними; 4. Свойства пределов функции; 5. Предел функции в точке; 6. Алгоритм раскрытия неопределенности вида 7. Алгоритм раскрытия неопределенности вида Содержание работы: 1. Вычисление пределов в точке; 2. Вычисление пределов с помощью алгоритма раскрытия неопределенности вида 3. Вычисление пределов с помощью алгоритма раскрытия неопределенности вида Литература: [1, с. 193-211] Порядок выполнения задания: Для выполнения первого задания, а именно, вычислить предел функции в какой-либо точке, необходимо подставить данную точку в функцию и получить числовое значение. Пример: Вычислить предел функции Решение: Подставляем
Ответ: При выполнении третьего, шестого, восьмого заданий используется алгоритм раскрытия неопределенности вида 1) Выявление старшей степени переменной. 2) Деление на выявленную переменную как числителя, так и знаменателя. 3) Вычисление предела, учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина. Пример: Вычислить предел функции Решение: Подставляем бесконечность в функцию Чтобы найти предел надо раскрыть неопределенность. Для этого сначала смотрим на числитель и находим
Ответ:
При выполнении второго, четвертого, пятого, седьмого заданий используется алгоритм раскрытия неопределенности вида 1) Разложение на множители числителя и знаменателя. 2) Сокращение дроби. 3) Вычисление значение предела Перечислим наиболее распространенные приемы разложения многочленов на множители: · Вынесение общего множителя за скобку. В том случае когда все члены многочлена имеют один и тот же общий множитель, его можно вынести за скобку, получая тем самым разложение многочлена Пример: Разложить на множители многочлен Решение: Каждое слагаемое этого многочлена содержит множитель · Применение формул сокращенного умножения. Полезно помнить следующие формулы:
Пример: Разложить на множители многочлен Решение: Разложим разность четвертых по формуле приведенной выше: · Группировка. Метод группировки слагаемых, как правило, применяется совместно с другими методами разложения на множители и чаще всего с методом вынесения за скобки. Суть метода состоит в том, что все слагаемые данного многочлена перегруппировываются таким образом, чтобы в каждой группе, возможно после вынесения общего множителя за скобки, образовалось бы одно и то же выражение. Это выражение можно также вынести за скобки как общий для всех групп множитель. Пример: Разложить на множители Решение:
· Разложение на множители квадратного трехчлена. Квадратный трехчлен Таким образом, разложение на множители квадратного трехчлена сводится к решению квадратного уравнения Пример: Разложить квадратный трехчлен Решение: Найдем корни квадратного уравнения
Дискриминант уравнения равен
Таким образом,
Пример: Вычислить предел Решение: Подставляя единицу вместо Разложим выражения в числителе и знаменателе на множители. Для того, чтобы разложить числитель на множители необходимо решить квадратное уравнение
Находим дискриминант по формуле Далее находим корни по формуле
Используя формулу разложения квадратного трехчлена на множители: Для того чтобы разложить знаменатель на множители используем формулу сокращенного умножения, а именно: Следовательно,
Итак, Ответ:
Практическая работа № 2 Практическая работа № 3 Практическая работа № 4 Практическая работа № 5 Практическая работа № 6 Практическая работа № 7 Практическая работа № 8 Практическая работа № 9 Практическая работа № 10 Операции над множествами Время проведения – 2 часа. Цель работы: формирование умений выполнять действия над множествами; Вопросы для подготовки к работе: 1. Понятие множества, подмножества; 2. Принадлежность элемента множеству; 3. Равенство множеств; 4. Пустое множество; 5. Конечное множество; 6. Бесконечное множество; 7. Дополнение множества; 8. Включение подмножества в множество; 9. Способы задания множеств; 10. Диаграмма Эйлера-Венна; 11. Операции над множествами. Содержание работы: 1. Задание множеств; 2. Выполнение операций над множествами. Порядок выполнения задания: При решении первого задания необходимо множество задать перечислением всех своих элементов – это один из способов задания множеств, если оно конечно. Пример: Множество Решение: Найдем множество действительных решений уравнения
Все корни уравнения действительные, то есть удовлетворяют условию Ответ: Пример: Множество Решение: Решим неравенство
Найдем корни квадратного трехчлена:
Решением неравенства Итак, согласно условию Ответ: Для выполнения второго, третьего заданий используются понятия объединения, пересечения, разности, равенства, дополнения множеств, диаграмма Эйлера-Венна. Пример: Даны множества Решение: Определим элементы множества Для построения диаграммы Венна рассмотрим, как связаны между собой множества
C
Определим элементы множества Строим диаграмму Венна:
C
Вариант 1 1. Множества задать перечислением всех своих элементов 1) 2) 2. Даны множества 3. Даны множества
Вариант 2 1. Множества задать перечислением всех своих элементов 1) 2) 2. Даны множества 3. Даны множества
ЛИТЕРАТУРА: Основные источники: 1. Богомолов Н. В., Самойленко П. И. Математика: Учебное пособие для техникумов, 7-е издание. - М.: Дрофа, 2010. – 400 с. 2. Богомолов Н.В. Сборник задач по математике: учеб. пособие для ссузов / Н.В. Богомолов.-М.: Дрофа, 2010. - 204 с. Дополнительные источники: 1. Мордкович А. Г. Алгебра и начала математического анализа. 10—11 классы. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) / А. Г. Мордкович. — 10-е изд., стер. — М.: Мнемозина, 2009. — 399 с. 2. Филимонова Е.В. Математика: Учебное пособие для средних специальных учебных заведений.- Ростов н/Д: Феникс, 2005.- 416с. (Серия «Среднее профессиональное образование»). МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ для выполнения практических работ по дисциплине «Математика»
Для специальностей: 42.02.01 Реклама
Пермь 2014 Методические рекомендации для выполнения практических работ по дисциплине «Математика» предназначены для студентов специальности 42.02.01 «Реклама».
Рассмотрено на заседании ЦМК преподавателей общеобразовательных дисциплин Председатель ЦМК Дозморов В.А.
Утверждено научно-методическим советом ПТПТД Зам. директора по НМР Рогова М.Н.
Составитель:Калинина Наталья Сергеевна, преподаватель математики КГАПОУ Пермского техникума профессиональных технологий и дизайна ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Методические рекомендации на выполнение практических работ по дисциплине «Математика» предназначены для обучающихся по основной профессиональной образовательной программе 42.02.01 «Реклама». Практические работы направлены на экспериментальное подтверждение теоретических положений и формирование учебных, профессиональных практических умений, общих и профессиональных компетенций обучающихся и составляют важную часть их профессиональной подготовки. Практические занятия способствуют интеграции мыслительной и практической деятельности обучающихся, развитию коммуникативных способностей, профессиональной самостоятельности и мобильности. В процессе практического занятия обучающиеся выполняют практическую работу под руководством преподавателя в соответствии с изучаемым содержанием учебного материала рабочих учебных программ по дисциплине. Данные методические рекомендации ориентированы на то, что в учебном процессе практические занятия являются основными видами учебных занятий, а практические работы выступают в качестве предметно-содержательной составляющей учебного занятия. Целями проведения практических занятий являются: обобщение, систематизацию, углубление, закрепление полученных теоретических знаний по конкретным темам дисциплины «Математика»; формирование умений применять полученные знания на практике, реализацию единства интеллектуальной и практической деятельности; выработку при решении поставленных задач таких профессионально значимых качеств, как самостоятельность, ответственность, точность, творческая инициатива. Каждая практическая работа состоит их двух частей: задания для подготовки к работе и задания для ее выполнения. Поэтому перед занятием студент должен повторить пройденный материал, используя конспекты лекций, и рекомендуемую литературу, указанную в задании к каждой работе, а также ознакомиться с основными сведениями, приведенными в данной работе. Практические работы выполняются обучающимися индивидуально. Отчет по каждой работе составляется каждым обучающимся самостоятельно. Отчет должен быть составлен по следующей примерной форме: - дата; - наименование темы; - цель работы; - ответы на вопросы для подготовки к работе; - содержание работы;
Практическая работа № 1 Раскрытие неопределенности вида Время проведения – 2 часа. Цель работы: научиться вычислять пределы функций путем раскрытия неопределенностей вида Вопросы для подготовки к работе: 1. Понятие предела последовательности; 2. Понятие предела функции; 3. Бесконечно малые и бесконечно большие, связь между ними; 4. Свойства пределов функции; 5. Предел функции в точке; 6. Алгоритм раскрытия неопределенности вида 7. Алгоритм раскрытия неопределенности вида Содержание работы: 1. Вычисление пределов в точке; 2. Вычисление пределов с помощью алгоритма раскрытия неопределенности вида 3. Вычисление пределов с помощью алгоритма раскрытия неопределенности вида Литература: [1, с. 193-211] Порядок выполнения задания: Для выполнения первого задания, а именно, вычислить предел функции в какой-либо точке, необходимо подставить данную точку в функцию и получить числовое значение. Пример: Вычислить предел функции Решение: Подставляем
Ответ: При выполнении третьего, шестого, восьмого заданий используется алгоритм раскрытия неопределенности вида 1) Выявление старшей степени переменной. 2) Деление на выявленную переменную как числителя, так и знаменателя. 3) Вычисление предела, учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина. Пример: Вычислить предел функции Решение: Подставляем бесконечность в функцию Чтобы найти предел надо раскрыть неопределенность. Для этого сначала смотрим на числитель и находим
Ответ:
При выполнении второго, четвертого, пятого, седьмого заданий используется алгоритм раскрытия неопределенности вида 1) Разложение на множители числителя и знаменателя. 2) Сокращение дроби. 3) Вычисление значение предела Перечислим наиболее распространенные приемы разложения многочленов на множители: · Вынесение общего множителя за скобку. В том случае когда все члены многочлена имеют один и тот же общий множитель, его можно вынести за скобку, получая тем самым разложение многочлена Пример: Разложить на множители многочлен Решение: Каждое слагаемое этого многочлена содержит множитель · Применение формул сокращенного умножения. Полезно помнить следующие формулы:
Пример: Разложить на множители многочлен Решение: Разложим разность четвертых по формуле приведенной выше: · Группировка. Метод группировки слагаемых, как правило, применяется совместно с другими методами разложения на множители и чаще всего с методом вынесения за скобки. Суть метода состоит в том, что все слагаемые данного многочлена перегруппировываются таким образом, чтобы в каждой группе, возможно после вынесения общего множителя за скобки, образовалось бы одно и то же выражение. Это выражение можно также вынести за скобки как общий для всех групп множитель. Пример: Разложить на множители Решение:
· Разложение на множители квадратного трехчлена. Квадратный трехчлен Таким образом, разложение на множители квадратного трехчлена сводится к решению квадратного уравнения Пример: Разложить квадратный трехчлен Решение: Найдем корни квадратного уравнения
Дискриминант уравнения равен
Таким образом,
Пример: Вычислить предел Решение: Подставляя единицу вместо Разложим выражения в числителе и знаменателе на множители. Для того, чтобы разложить числитель на множители необходимо решить квадратное уравнение
Находим дискриминант по формуле Далее находим корни по формуле
Используя формулу разложения квадратного трехчлена на множители: Для того чтобы разложить знаменатель на множители используем формулу сокращенного умножения, а именно: Следовательно,
Итак, Ответ:
|

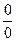 и
и 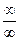
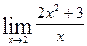
 в функцию
в функцию 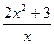 и находим значение выражения, т.е.
и находим значение выражения, т.е.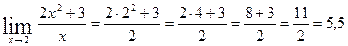
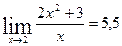

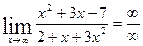 - это предел на неопределенность вида
- это предел на неопределенность вида 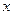 в старшей степени - старшая степень в числителе равна двум, затем смотрим на знаменатель и тоже находим
в старшей степени - старшая степень в числителе равна двум, затем смотрим на знаменатель и тоже находим 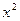 . Получим:
. Получим: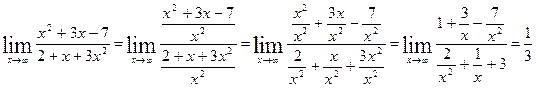


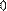
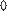



 Величины
Величины  являются бесконечно малыми при
являются бесконечно малыми при 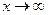 и их пределы равны нулю.
и их пределы равны нулю.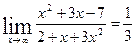

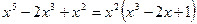

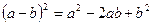

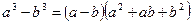

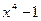
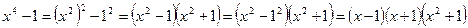
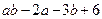
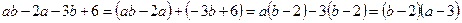
 раскладывается на два линейных множителя:
раскладывается на два линейных множителя:  , где
, где 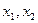 являются корнями уравнения
являются корнями уравнения 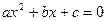
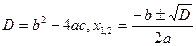
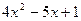 на множители.
на множители.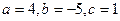
 , следовательно
, следовательно
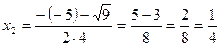

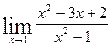
 в числитель и знаменатель получим:
в числитель и знаменатель получим: 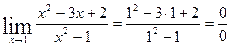 , то есть имеем неопределенность вида
, то есть имеем неопределенность вида  .
.
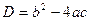 , получаем:
, получаем: 

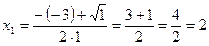
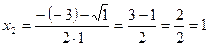
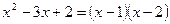 . Числитель на множители разложен.
. Числитель на множители разложен. . Получаем:
. Получаем:  . Знаменатель на множители разложен.
. Знаменатель на множители разложен. Сократим данную дробь на скобку
Сократим данную дробь на скобку 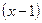 :
: Теперь подставляем
Теперь подставляем  в выражение, которое осталось под знаком предела:
в выражение, которое осталось под знаком предела: 
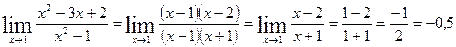

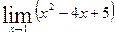 2.
2. 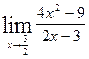 3.
3.  4.
4. 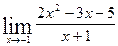 5.
5. 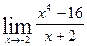 6.
6. 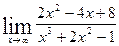 7.
7. 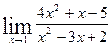 8.
8. 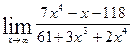
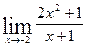 2.
2. 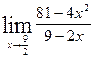 3.
3. 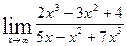 4.
4. 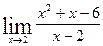 5.
5. 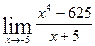 6.
6. 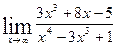 7.
7.  8.
8. 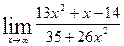
 задать перечислением всех своих элементов.
задать перечислением всех своих элементов.
 или
или 


 , следовательно
, следовательно 
 задать перечислением всех своих элементов.
задать перечислением всех своих элементов. методом интервалов
методом интервалов











 -1,5
-1,5
 , то есть
, то есть 
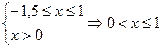 , отметим, что из данного промежутка действительным числам принадлежит только
, отметим, что из данного промежутка действительным числам принадлежит только  - множество из одного элемента.
- множество из одного элемента. . Найдите множества
. Найдите множества  и
и  . Составьте диаграммы Венна.
. Составьте диаграммы Венна. . Элементы
. Элементы  и
и  одновременно принадлежат множеству
одновременно принадлежат множеству  и
и  , следовательно,
, следовательно,  . Аналогично
. Аналогично  . Таким образом, объединение
. Таким образом, объединение  .
.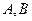 и
и 

 A B
A B

 X
X . Универсальное множество по условию задания состоит из 26 букв
. Универсальное множество по условию задания состоит из 26 букв  . Если отсюда исключить пять элементов множества
. Если отсюда исключить пять элементов множества  из двадцати одноИго элемента
из двадцати одноИго элемента  . Пересечение множеств
. Пересечение множеств  состоит из элементов
состоит из элементов  , то есть всех элементов множества
, то есть всех элементов множества  вычеркнем из множества
вычеркнем из множества  элементы
элементы  , принадлежащие
, принадлежащие  . Получим
. Получим  . В итоге
. В итоге  .
.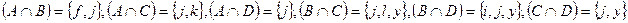



 A B
A B




 Y
Y

 D
D

 . Найдите множества
. Найдите множества  и
и  . Найдите множества
. Найдите множества 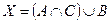 и
и  . Составьте диаграммы Венна.
. Составьте диаграммы Венна.

 . Найдите множества
. Найдите множества  и
и  . Составьте диаграммы Венна.
. Составьте диаграммы Венна. . Найдите множества
. Найдите множества  и
и  . Составьте диаграммы Венна.
. Составьте диаграммы Венна.


