
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Действия с комплексными числамиСодержание книги Поиск на нашем сайте
Время проведения – 2 часа. Цель работы: отработать навыки выполнения действий с комплексными числами; научиться решать квадратные уравнения, дискриминант которых отрицателен. Вопросы для подготовки к работе: 1. Понятие мнимой единицы; 2. Понятие комплексного числа; 3. Понятие модуля и аргумента комплексного числа; 4. Равенство комплексных чисел; 5. Решение квадратных уравнений, дискриминант которых отрицателен; 6. Действие над комплексными числами в алгебраической форме; 7. Геометрическая интерпретация комплексного числа; 8. Тригонометрическая форма комплексного числа; Содержание работы: 1. Решение квадратных уравнений, дискриминант которых отрицателен; 2. Выполнение действий над комплексными числами; 3. Геометрическая интерпретация комплексного числа; 4. Представление комплексного числа в тригонометрической форме. Литература: [1, с.17-23] Порядок выполнения задания: При выполнении первого задания необходимо учитывать следующее: в комплексных числах можно извлечь квадратный корень из отрицательного числа, так как Пример: Решить уравнение Решение: Найдем дискриминант
Ответ: Для выполнения второго, третьего заданий необходимо уметь применять операции над комплексными числами и знать правило равенства комплексных чисел. Отметим, что с комплексными числами, записанными в алгебраической форме, операции сложения, вычитания и умножения можно производить также, как с действительными биномами, деление выполняют путем умножения делимого и делителя на число, сопряженное делителю. Правило равенства: два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей. Пример: Найдите сумму, разность, произведение, частное двух комплексных чисел Решение:
Ответ: Пример: Найдите действительные решения уравнения Решение:
В соответствии с правилом равенства получаем:
Ответ: Для выполнения четвертого, пятого заданий необходимо знать тригонометрическую форму записи комплексного числа и его геометрическую интерпретацию. Геометрическая интерпретация комплексных чисел состоит в том, что каждому комплексному числу
Расстояние Пример: Изобразить на комплексной плоскости число Решение: Комплексному числу
Для комплексного числа Поэтому в тригонометрической форме комплексное число имеет вид: Ответ: Вариант 1 1. Решить уравнение 1) 2) 3) 4) 2. Выполнить действия над комплексными числами, представив результат в алгебраической форме 1) 2) 3) 4) 5) 6) 7) 3. Найти действительные решения уравнения 1) 2) 4. Изобразите на комплексной плоскости следующие комплексные числа 1) 2) 5. Записать комплексное число
Вариант 2 1. Решить уравнение 1) 2) 3) 4) 2. Выполнить действия над комплексными числами, предствавив результат в алгебраической форме 1) 2) 3) 4) 5) 6) 7) 3. Найти действительные решения уравнения 1) 2) 4. Изобразите на комплексной плоскости следующие комплексные числа 1) 2) 5. Записать комплексное число
Практическая работа № 8
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1932; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.116.77 (0.007 с.) |

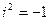 , где
, где  - мнимая единица. Следовательно, в поле комплексных чисел разрешимо любое квадратное уравнение, в том числе с отрицательным дискриминантом.
- мнимая единица. Следовательно, в поле комплексных чисел разрешимо любое квадратное уравнение, в том числе с отрицательным дискриминантом.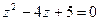
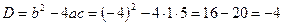 ,
,  , следовательно, уравнение имеет мнимые корни, которые находят по формуле
, следовательно, уравнение имеет мнимые корни, которые находят по формуле 


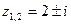


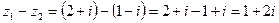
 , где
, где 

 ,
,  ,
, 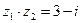 ,
, 


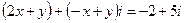

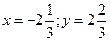
 ставится в соответствие точка М
ставится в соответствие точка М  координатной плоскости таким образом, что действительная часть комплексного числа представляет собой абсциссу (ось
координатной плоскости таким образом, что действительная часть комплексного числа представляет собой абсциссу (ось  называют действительной), а коэффициент при мнимой части – ординату точки (ось
называют действительной), а коэффициент при мнимой части – ординату точки (ось  называют мнимой).
называют мнимой). y
y

 b
b
 М
М
 r
r
 0
0
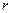 от начала системы координат до точки, соответствующей комплексному числу
от начала системы координат до точки, соответствующей комплексному числу 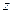 , называют модулем этого числа, который вычисляют по формуле:
, называют модулем этого числа, который вычисляют по формуле: 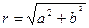 . Угол
. Угол  между положительной полуосью
между положительной полуосью  называют аргументом комплексного числа
называют аргументом комплексного числа  называют тригонометрической формой комплексного числа.
называют тригонометрической формой комплексного числа. и записать его в тригонометрической форме.
и записать его в тригонометрической форме.
 y
y

 1
1
 0
0
 ,
,  (по чертежу).
(по чертежу).














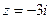
 в тригонометрической форме
в тригонометрической форме

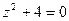

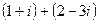










 в тригонометрической форме
в тригонометрической форме


