
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение систем линейных уравнений по формулам КрамераСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Время проведения – 2 часа. Цель работы: научиться решать системы линейных уравнений методом Крамера; Вопросы для подготовки к работе: 1. Понятие системы линейных уравнений; 2. Совместные и несовместные системы линейных уравнений; 3. Понятие матрицы; 4. Понятие определителя матрицы; 5. Формула определителя второго порядка; 6. Формула определителя третьего порядка; 7. Свойства определителя n-го порядка; 8. Решение систем линейных уравнений методом Крамера; Содержание работы: 1. Нахождение определителя матрицы; 2. Решение систем линейных уравнений методом Крамера. Порядок выполнения задания: При выполнении первого задания используются формулы для вычисления определителей первого и второго порядка, а также правило разложения определителя n-го порядка по строке или столбцу. Пусть задана квадратная матрица второго порядка
Пример: Вычислить определитель Решение: Имеем определитель второго порядка. Используем формулу, указанную выше.
Ответ: Пусть задана квадратная матрица третьего порядка
Определитель третьего порядка вычислить легко, если учесть следующее правило: со знаком плюс идут произведения троек чисел, расположенных на главной диагонали матрицы, и в вершинах треугольников с основанием параллельным этой диагонали и вершиной противоположного угла матрицы. Со знаком минус идут тройки из второй диагонали и из треугольников, построенных относительно этой диагонали. Это правило называют правилом треугольников. Пример: Вычислить определитель Решение: Имеем определитель третьего порядка, для его вычисления воспользуемся правилом треугольников:
Ответ: Для определителей четвертого и более высоких порядков обычно применяют разложение по элементам строки или столбца. Определитель равен сумме произведений элементов строки определителя на их алгебраическое дополнение (число
Пример: Вычислить определитель Решение: Используем формулу разложения по элементам второй строки:
Ответ: При решении второго задания используется метод Крамера – способ решения квадратных систем линейных уравнений, который основан на следующей теореме Крамера: если определитель матрицы квадратной системы не равен нулю, то система совместна и имеет единственное решение, которое находится по формулам Крамера: Пример: Найдите решение системы линейных Решение: Вычисляем определитель матрицы системы по формуле:
Имеем,
Так как
Аналогично, определитель
Тогда получаем:
Ответ: Пример: Найдите решение системы линейных уравнений методом Крамера Решение: Перепишем систему в виде
Имеем,
Определитель основной матрицы отличен от нуля, следовательно. система линейных уравнений имеет единственное решение. Найдем его методом Крамера. Вычислим определители
Таким образом,
Ответ: Пример: Найдите решение системы линейных уравнений методом Крамера Решение: Вычислим определитель основной матрицы системы, разложив его по элементам второй строки:
Определитель основной матрицы системы отличен от нуля, поэтому для решения системы можно воспользоваться методом Крамера. Найдем
Аналогично вычисляются:
Таким образом,
Ответ:
Практическая работа № 9
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 675; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.86.112 (0.011 с.) |

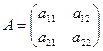 . Определитель этой матрицы (определитель второго порядка) вычисляется следующим образом:
. Определитель этой матрицы (определитель второго порядка) вычисляется следующим образом: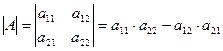

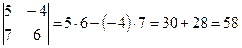
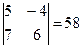
 . Определитель этой матрицы (определитель третьего порядка) вычисляется следующим образом:
. Определитель этой матрицы (определитель третьего порядка) вычисляется следующим образом:

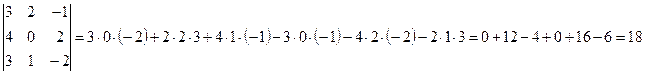
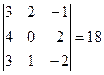
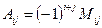 , где
, где 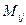 - минор к элементу
- минор к элементу  определителя
определителя  порядка, то есть определитель
порядка, то есть определитель 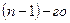 порядка, полученный из исходного вычеркиванием
порядка, полученный из исходного вычеркиванием  строки и
строки и 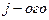 столбца). Обычно выбирают ту строку/столбец, в которой/ом есть нули.
столбца). Обычно выбирают ту строку/столбец, в которой/ом есть нули.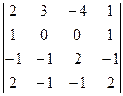
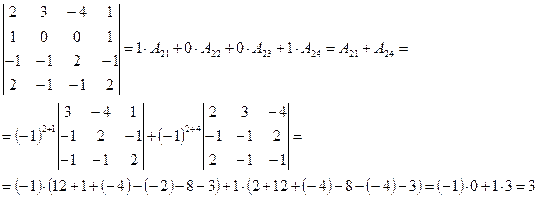
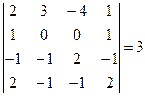
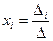 , где
, где 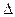 - определитель матрицы системы,
- определитель матрицы системы,  - определитель матрицы системы, где вместо
- определитель матрицы системы, где вместо 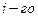 столбца стоит столбец правых частей.
столбца стоит столбец правых частей. уравнений при помощи метода Крамера.
уравнений при помощи метода Крамера.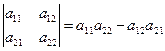
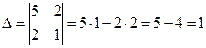
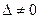 , то по Теореме Крамера система совместна и имеет единственное решение. Вычислим вспомогательные определители. Определитель
, то по Теореме Крамера система совместна и имеет единственное решение. Вычислим вспомогательные определители. Определитель 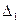 получим из определителя
получим из определителя 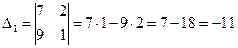
 получается из определителя матрицы системы
получается из определителя матрицы системы 
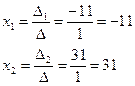
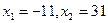

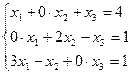 , чтобы стало видно основную матрицу системы
, чтобы стало видно основную матрицу системы  . Найдем ее определитель по формуле:
. Найдем ее определитель по формуле:
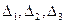 .
.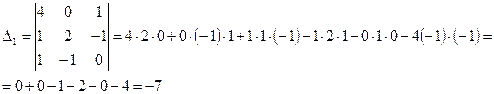
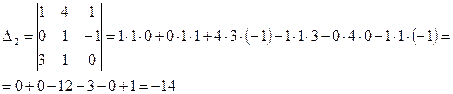

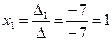
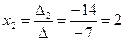
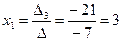

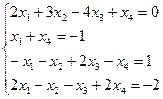
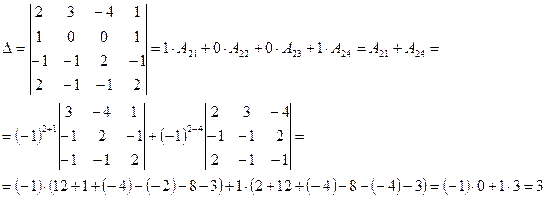
 .
.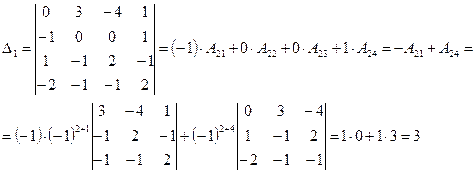
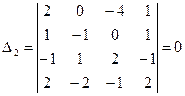
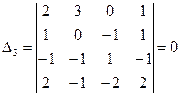
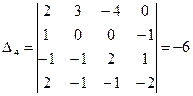
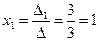
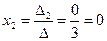

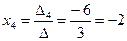
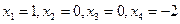
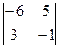 2)
2) 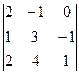 3)
3) 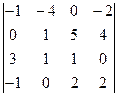 2. Решите системы линейных уравнений методом Крамера:
1)
2. Решите системы линейных уравнений методом Крамера:
1) 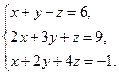 2)
2) 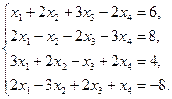 3)
3) 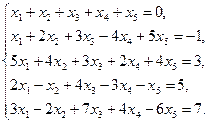 4)
4) 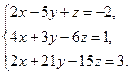 5)
5) 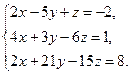
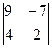 2)
2) 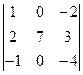 3)
3)  2. Решите системы линейных уравнений методом Крамера:
1)
2. Решите системы линейных уравнений методом Крамера:
1) 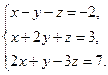 2)
2)  3)
3)  5)
5) 


