
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы решения систем линейных уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Матричный способ решения СЛУ
Рассмотрим систему n линейных уравнений с n неизвестными
Пусть основная матрица системы невырожденная, т.е. Данную систему линейных уравнений можно записать в матричной форме
где Покажем, что такая система имеет решение, и притом единственное, и найдем его. Так как
Итак, формула
является матричной записью решения рассматриваемой системы. Единственность решения следует из единственности обратной матрицы.
Пример 5.1. Решить СЛУ матричным способом
Решение. Запишем основную матрицу и матрицы-столбцы, составленные из неизвестных и свободных членов:
СЛУ в матричной форме имеет вид: Находим
Находим алгебраические дополнения каждого элемента основной матрицы:
Составляем обратную матрицу:
Далее получаем решение СЛУ:
, Формулы Крамера
Рассмотрим систему n линейных уравнений с n неизвестными
Определитель системы обозначим
Обозначим через
где k - одно из чисел 1, 2, …, n. Теорема 5.1. (Теорема Крамера) Если определитель системы отличен от нуля, то система имеет единственное решение, которое находится по формулам
где
Теорему 5.1. примем без доказательства. Формулы (5.4) называются формулами Крамера. Из теоремы Крамера следует: если однородная система имеет решение, то ее определитель
Пример 5.2. Решить СЛУ по формулам Крамера
Решение. Находим
Далее получаем решение:
,
Метод Гаусса
Метод Гаусса является исторически первым наиболее распространенным точным методом решения системы линейных уравнений. Сущность этого метода состоит в том, что посредством элементарных преобразований данная система приводится к специальному виду, из которого все решения системы непосредственно усматриваются.
Рассмотрим СЛУ (5.5), содержащую из m уравнений и n неизвестных:
Метод Гаусса или метод последовательного исключения неизвестных, применяемый для решения системы (5.5), состоит в следующем. Пусть в системе коэффициент
где Предполагая, что 1)
где 2)
где 3)
где Запись системы, полученной после преобразований, называют ступенчатой (в частности, при Система (5.7) имеет единственное решение. Из последнего уравнения Система (5.8) имеет бесчисленное множество решений. Из последнего уравнения можно выразить одно из неизвестных (например,
Полученная система представляет собой общее решение исходной системы. Неизвестные Система (5.9) не имеет решений, так как эта система несовместна, т.е. никакие значения неизвестных не могут удовлетворять ее последнему уравнению. Итак, метод последовательного исключения неизвестных применим к любой системе линейных уравнений. Решая систему этим методом, преобразования можно совершать не над самими уравнениями, а над расширенной матрицей.
Пример 5.3. Решить СЛУ методом Гаусса:
Решение. Составляем расширенную матрицу:
Сначала поменяем местами первую и третью строки, получаем:
Поскольку во второй строке первый элемент равен нулю, то элементы второй строки не изменяем. Умножаем элементы первой строки на
Теперь поменяем местами вторую и третью строки:
Умножаем элементы второй строки на
По коэффициентам последней матрицы составляем систему, равносильную исходной системе:
Из последнего уравнения находим , Пример 5.4. Решить систему уравнений
Решение. Составляем расширенную матрицу:
Сначала поменяем местами первую и третью строки, чтобы первый элемент (для удобства) был равен 1. Этот элемент будет разрешающим.
[вторую и третью строки умножим на (-1)] ~ По коэффициентам последней матрицы составляем систему, равносильную исходной системе:
Из последнего уравнения находим , Пример 5.5. Решить систему уравнений
Решение. Составляем расширенную матрицу и преобразуем ее:
Система несовместна, так как последняя матрица содержит строку, соответствующую уравнению, в котором все коэффициенты при неизвестных равны нулю, а свободный член отличен от нуля. , Пример 5.6. Решить систему уравнений
Решение. Составляем расширенную матрицу и преобразуем ее:
~ Исходная система свелась к ступенчатой:
Из последнего уравнения за базисную неизвестную выберем, например,
Таким образом, получаем общее решение системы:
Пусть
где ,
5.3.Исследование СЛУ
Как уже отмечалось, метод Гаусса применим к любой системе линейных уравнений. Этот метод позволяет выяснить, совместна ли данная система; с его помощью находятся все решения совместной линейной системы. Исследование систем линейных уравнений можно осуществлять с помощью других методов, основанных на теоремах, которые приводятся без доказательства.
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1771; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

 .
. . Определитель
. Определитель  называется определителем системы.
называется определителем системы. ,
, - матрица-столбец, составленная из неизвестных,
- матрица-столбец, составленная из неизвестных,  - матрица-столбец, составленная из свободных членов.
- матрица-столбец, составленная из свободных членов. . Умножив обе части уравнения
. Умножив обе части уравнения  Û
Û  Û
Û  .
. (5.3)
(5.3) .
. ,
,  ,
,  .
. :
: .
. ;
;  ;
;  ;
; ;
;  ;
;  ;
;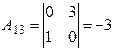 ;
;  ;
;  .
. .
. .
. .
. :
: .
. определитель, полученный заменой в определителе
определитель, полученный заменой в определителе  столбца из коэффициентов при неизвестной
столбца из коэффициентов при неизвестной  столбцом свободных членов системы, т.е.
столбцом свободных членов системы, т.е. ,
, , (5.4)
, (5.4) .
. :
: ;
;  ;
; ;
;  .
. .
. . (5.5)
. (5.5) , который называется разрешающим коэф-фициентом. Если
, который называется разрешающим коэф-фициентом. Если  , то на первое место можно поставить уравнение, в котором коэффициент при неизвестной
, то на первое место можно поставить уравнение, в котором коэффициент при неизвестной  отличен от нуля. Умножаем первое уравнение системы (5.5) на
отличен от нуля. Умножаем первое уравнение системы (5.5) на  и прибавляем ко второму, получаем уравнение, в котором коэффициент при
и прибавляем ко второму, получаем уравнение, в котором коэффициент при  и прибавляем к третьему, получаем уравнение, также не содержащее члена с
и прибавляем к третьему, получаем уравнение, также не содержащее члена с  -ом уравнении коэффициент при
-ом уравнении коэффициент при  , (5.6)
, (5.6) - некоторые новые коэффициенты при неизвестных,
- некоторые новые коэффициенты при неизвестных,  - новые свободные члены.
- новые свободные члены. , который становится разрешающим коэффициентом, и, оставляя неизменными первые два уравнения системы (5.6), преобразуем ее так, чтобы в каждом из остальных уравнений коэффициент при
, который становится разрешающим коэффициентом, и, оставляя неизменными первые два уравнения системы (5.6), преобразуем ее так, чтобы в каждом из остальных уравнений коэффициент при  обратился в нуль. Продолжая этот процесс, систему (5.6) можно привести к одной из следующих систем:
обратился в нуль. Продолжая этот процесс, систему (5.6) можно привести к одной из следующих систем: , (5.7)
, (5.7) и
и  .
. , (5.8)
, (5.8) и
и  .
. , (5.9)
, (5.9) .
. находим
находим  :
:  . Из предпоследнего уравнения находим
. Из предпоследнего уравнения находим  , затем из третьего от конца -
, затем из третьего от конца -  . Двигаясь, таким образом, снизу вверх, найдем значения всех неизвестные. Процесс преобразования системы (5.5) к одному из видов (5.7), (5.8) или (5.9) называют прямым ходом метода Гаусса, а описанную только что процедуру движения снизу вверх по уравнениям системы (5.7) с целью получения значений неизвестных – обратным ходом.
. Двигаясь, таким образом, снизу вверх, найдем значения всех неизвестные. Процесс преобразования системы (5.5) к одному из видов (5.7), (5.8) или (5.9) называют прямым ходом метода Гаусса, а описанную только что процедуру движения снизу вверх по уравнениям системы (5.7) с целью получения значений неизвестных – обратным ходом. неизвестных (
неизвестных ( ), входящих в это уравнение. Полученное значение
), входящих в это уравнение. Полученное значение  через эти неизвестные и т.д. И, наконец, выражаем
через эти неизвестные и т.д. И, наконец, выражаем  . (5.10)
. (5.10) - базисными. Свободным неизвестным можно придавать любые числовые значения и по формулам (5.10) находить соответствующие значения базисных неизвестных. Каждый раз будет получаться определенное частное решение исходной системы. Заметим, что частное решение, получаемое из общего при нулевых значениях свободных неизвестных, называются базисным решением системы, которое играет исключительную роль в математическом программировании.
- базисными. Свободным неизвестным можно придавать любые числовые значения и по формулам (5.10) находить соответствующие значения базисных неизвестных. Каждый раз будет получаться определенное частное решение исходной системы. Заметим, что частное решение, получаемое из общего при нулевых значениях свободных неизвестных, называются базисным решением системы, которое играет исключительную роль в математическом программировании. .
. .
. и складываем с соответствующими элементами третьей строки:
и складываем с соответствующими элементами третьей строки: .
. .
. и складываем с соответствующими элементами третьей строки, получаем:
и складываем с соответствующими элементами третьей строки, получаем: .
. .
. , из второго –
, из второго –  и из первого –
и из первого –  . Итак, исходная система имеет единственное решение
. Итак, исходная система имеет единственное решение 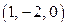 .
. .
. .
. ~
~  ~
~ ~
~  .
. .
. , из второго –
, из второго –  и из первого –
и из первого –  . Итак, исходная система имеет единственное решение
. Итак, исходная система имеет единственное решение  .
. .
. ~
~  ~
~  .
. .
. ~
~  ~
~  ~
~ .
. .
. :
:  . Подставляем
. Подставляем  .
. .
. , где
, где  - любые действительные числа. Тогда получаем следующее решение
- любые действительные числа. Тогда получаем следующее решение ,
,


