
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы линейных алгебраических уравнений, общие понятия. Различные методы решения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
Упорядоченный набор значений СЛАУ называется совместной, если она имеет, хотя бы одно решение. В противном случае система называется несовместной. Будем рассматривать системы из p линейных алгебраических уравнений с n неизвестными переменными (p может быть равно n) вида
В матричной форме записи эта система уравнений имеет вид
Решением системы линейных алгебраических уравнений называют набор значений неизвестных переменных Если система уравнений имеет хотя бы одно решение, то она называется совместной. Если система уравнений решений не имеет, то она называется несовместной. Если СЛАУ имеет единственное решение, то ее называют определенной; если решений больше одного, то – неопределенной. Если свободные члены всех уравнений системы равны нулю, то система называется однородной, в противном случае – неоднородной. Решение систем линейных уравнений методом Гаусса. Правило Крамера решения систем линейных уравнений Рассмотрим невырожденные системы линейных уравнений, т.е. системы, у которых Пусть дана система двух линейных уравнений с двумя неизвестными:
Коэффициенты этой системы составляют квадратную матрицу второго порядка:
Решим систему (13.3). Для этого умножим первое уравнение системы на
Аналогично, исключая Если Общий знаменатель значений неизвестных Мы получили правило Крамера решения системы двух линейных уравнений с двумя неизвестными. Правило Крамера. Если определитель Невырожденную систему линейных уравнений Поскольку матрица Мы ответили на три вопроса относительно систем линейных уравнений. Однако применение теоремы Крамера, которая позволила дать этот ответ, приводит к слишком громоздким вычислениям. Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса. Метод Гаусса Метод Гаусса основан на теореме: если к некоторому уравнению системы прибавить другое уравнение этой системы, умноженное на любое действительное число, или умножить любое уравнение системы на отличное от нуля действительное число, то полученная система будет эквивалентна исходной. Метод Гаусса называют также методом последовательного исключения неизвестных, осуществляя его за несколько итераций. На каждой итерации выбирается разрешающее уравнение и базисное неизвестное. В качестве разрешающего уравнения можно взять любое уравнение системы, которое ранее не было выбрано разрешающим и не все коэффициенты которого равны нулю. За базисное неизвестное выбирают неизвестное, коэффициент при котором в разрешающем уравнении, называемый разрешающим коэффициентом, не равен нулю. Алгоритм метода следующий: 1.Выбирают разрешающее уравнение и базисное неизвестное. 2.Делят обе части разрешающего уравнения на разрешающий коэффициент и исключают базисное неизвестное из всех уравнений системы, кроме разрешающего. Отбрасывают, если они появились, уравнения, все коэффициенты и свободный член в котором равны нулю. Если получилось уравнение, в котором коэффициенты нулевые, а свободный член не нуль, то система несовместна, конец. Если таких уравнений нет, то шаг 1. Если все уравнения были использованы в качестве разрешающих, то шаг 3.Если нет, то шаг 1. 4.Базисные неизвестные оставляют слева, а небазисные (назовем их свободными, так как они могут принимать любые значения) переносят вправо.
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 795; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |


 называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.
называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.
 - неизвестные переменные,
- неизвестные переменные,  - коэффициенты (некоторые действительные или комплексные числа),
- коэффициенты (некоторые действительные или комплексные числа),  - свободные члены (также действительные или комплексные числа). Такую форму записи СЛАУ называют координатной.
- свободные члены (также действительные или комплексные числа). Такую форму записи СЛАУ называют координатной.


 матрица-столбец неизвестных переменных, матрица-столбец свободных членов.
матрица-столбец неизвестных переменных, матрица-столбец свободных членов. , обращающий все уравнения системы в тождества. Матричное уравнение
, обращающий все уравнения системы в тождества. Матричное уравнение  при данных значениях неизвестных переменных также обращается в тождество
при данных значениях неизвестных переменных также обращается в тождество  .
. и определитель матрицы системы отличен от нуля. Определитель матрицы называется определителем системы. Следующая теорема, называемая правилом Крамера, отвечает на второй вопрос.
и определитель матрицы системы отличен от нуля. Определитель матрицы называется определителем системы. Следующая теорема, называемая правилом Крамера, отвечает на второй вопрос.
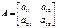
 , второе – на
, второе – на  и вычтем из первого уравнения второе:
и вычтем из первого уравнения второе: .
. , получим
, получим  .
. , то найдем единственное решение системы:
, то найдем единственное решение системы:  .
. и
и  , обозначаемый через
, обозначаемый через 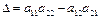 , называется определителем матрицы
, называется определителем матрицы  . Это определитель второго порядка. Числителями неизвестных
. Это определитель второго порядка. Числителями неизвестных  являются определители тоже второго порядка
являются определители тоже второго порядка  . Откуда
. Откуда  .
. системы
системы  линейных уравнений с
линейных уравнений с  неизвестными отличен от нуля, то система имеет единственное решение:
неизвестными отличен от нуля, то система имеет единственное решение:  , где
, где ‑ определитель, получаемый из
‑ определитель, получаемый из  заменой
заменой  -го столбца столбцом свободных членов.
-го столбца столбцом свободных членов. можно решить и иным способом.
можно решить и иным способом.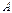 ‑ невырожденная, то для нее существует единственная обратная матрица
‑ невырожденная, то для нее существует единственная обратная матрица  . Умножив обе части уравнения
. Умножив обе части уравнения  слева на матрицу
слева на матрицу  , получим
, получим  , откуда
, откуда  .
.


