
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойство 1. При замене строк столбцами (транспонировании) значение определителя не изменитсяСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Свойство 2. Если хотя бы один ряд (строка или столбец) состоит из нулей, то определитель равен нулю. Доказательство очевидно. В самом деле, тогда в каждом члене определителя один из множителей будет нуль. Свойство 3. Если в определителе поменять местами два соседних параллельных ряда (строки или столбцы), то определитель поменяет знак на противоположный Свойство 4. Если в определителе имеются два одинаковых параллельных ряда, то определитель равен нулю Свойство 5. Если в определителе два параллельных ряда пропорциональны, то определитель равен нулю Свойство 6. Если все элементы определителя, стоящие в одном ряду, умножить на одно и то же число, то значение определителя изменится в это число раз Следствие. Общий множитель, содержащийся во всех элементах одного ряда, можно вынести за знак определителя Свойство 7. Если в определителе все элементы одного ряда представлены в виде суммы двух слагаемых, то он равен сумме двух определителей Свойство 8. Если к элементам какого-либо ряда прибавить произведение соответствующих элементов параллельного ряда на постоянный множитель, то значение определителя не изменится Свойство 9. Если к элементам i -го ряда прибавить линейную комбинацию соответствующих элементов нескольких параллельных рядов, то значение определителя не изменится Матрицы и линейные операции над ними. Произведение матриц, обратная матрица. Ранг матрицы. Матрицы одинаковой размерности называются равными, если у них соответственно равны элементы, стоящие на одинаковых местах. Матрица называется нулевой, если все ее элементы равны 0. Квадратная матрица называется единичной, если элементы, стоящие на ее главной диагонали, равны 1, а остальные равны 0. К линейным операциям над элементами множества или пространства относятся операции сложения элементов и их умножения на скаляр (число). Умножение матрицы на число Сложение матриц
Линейной комбинацией матриц A и B называется выражение вида αА+βВ, где α и β – числовые коэффициенты. Линейные операции над матрицами. 1. Сложение матриц. Суммой матриц А и В одинаковой размерности mXn называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах: Свойства сложения: 1. А + В = В + А. 2. (А + В) + С = А + (В + С). 3. Если О – нулевая матрица, то А + О = О + А = А Замечание 1. Справедливость этих свойств следует из определения операции сложения матриц. Замечание 2. Отметим еще раз, что складывать можно только матрицы одинаковой размерности. 2. Умножение матрицы на число. Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число. Свойства умножения матрицы на число: 1. (km)A=k(mA). 2. k(A + B) = kA + kB. 3. (k + m)A = kA + mA. Операции над матрицами Суммой двух матриц Сложение матриц обладает следующими свойствами: 1.Коммутативность, т.е. 2.Ассоциативность, т.е. 3.Для любых двух матриц Произведением матрицы Умножение матрицы на действительное число обладает следующими свойствами: 1. 4. 5. 6. Матрица Свойства умножения: 1.Если матрица
2. 3.Умножение матриц не коммутативно, т.е., как правило, Обратная матрица Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Матрица, обратная матрице А, обозначается через А 1 , так что В = А 1 . Обратная матрица вычисляется по формуле Вычисление обратной матрицы по формуле для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы. Ранг матрицы Рангом матрицы называется наибольший порядок ее миноров, отличных от нуля. Ранг матрицы A обозначают Если все миноры порядка Если все миноры первого порядка (элементы матрицы
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 780; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.99.16 (0.009 с.) |


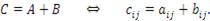
 и
и 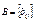 одинакового размера называется матрица
одинакового размера называется матрица 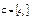 того же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т.е.
того же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т.е. 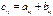 .
. .
.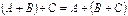 .
. и
и  одинакового размера существует единственная матрица
одинакового размера существует единственная матрица 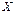 такая, что
такая, что  . Матрица
. Матрица 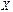 обозначается
обозначается 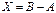 и называется разностью матриц
и называется разностью матриц 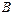 и
и 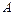 . Уравнение
. Уравнение 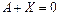 имеет решение
имеет решение  , получающаяся при этом матрица называется противоположной
, получающаяся при этом матрица называется противоположной 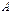 и обозначается
и обозначается 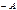 .
.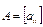 на число
на число  называется матрица, все элементы которой равны соответствующим элементам матрицы
называется матрица, все элементы которой равны соответствующим элементам матрицы 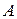 , умноженным на число
, умноженным на число  .
. ; 2.
; 2.  ; 3.
; 3. 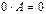 ;
; (ассоциативность);
(ассоциативность);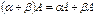 (дистрибутивность);
(дистрибутивность); (дистрибутивность).
(дистрибутивность).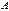 называется согласованной с матрицей
называется согласованной с матрицей  равно числу строк матрицы
равно числу строк матрицы 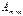 на матрицу
на матрицу 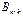 называется матрица
называется матрица  , где
, где 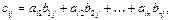
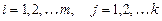 , т.е. элемент, стоящий в
, т.е. элемент, стоящий в  -той строке и
-той строке и  -том столбце матрицы произведения равен сумме произведений элементов
-том столбце матрицы произведения равен сумме произведений элементов 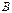 .
.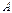 согласована с матрицей
согласована с матрицей 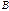 согласована с матрицей
согласована с матрицей 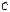 , то
, то 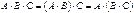 ‑ ассоциативность умножения;
‑ ассоциативность умножения;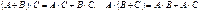 ‑ свойство дистрибутивности;
‑ свойство дистрибутивности; .
.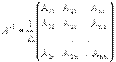 где А i j - алгебраические дополнения элементов a i j.
где А i j - алгебраические дополнения элементов a i j.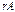 .
.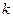 данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.
данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.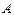 ) равны нулю, то
) равны нулю, то 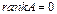 . Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то
. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то 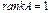 . Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка
. Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка 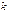 , окаймляющие ненулевой минор
, окаймляющие ненулевой минор 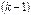 -го порядка равны нулю, либо таких миноров нет. Тогда
-го порядка равны нулю, либо таких миноров нет. Тогда 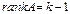 .
.


