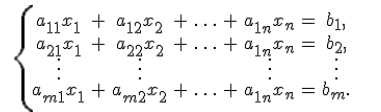Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители квадратной матрицы и их свойства.Содержание книги
Поиск на нашем сайте
Пусть А – квадратная матрица порядка n:
Каждой такой матрице можно поставить в соответствие единственное действительное число, называемое определителем (детерминантом) матрицы и обозначаемое
Рассмотрим правила вычисления определителей и их свойства для квадратных матриц второго и третьего порядка. Определителем второго порядка матрицы
Пример1.
Для обозначения матриц используют круглые или квадратные скобки, а для определителя – вертикальные линии. Матрица – это таблица чисел, а определитель – число. Из определения определителя второго порядка следуют его свойства: 1. Определитель не изменится при замене всех его строк соответствующими столбцами:
2. Знак определителя меняется на противоположный при перестановке строк (столбцов) определителя:
3. Общий множитель всех элементов строки (столбца) определителя можно вынести за знак определителя:
4. Если все элементы некоторой строки (столбца) определителя равны нулю, то определитель равен нулю. 5. Определитель равен нулю, если соответствующие элементы его строк (столбцов) пропорциональны:
Правило Саррюса или правило треугольника:
Пример 2. Вычислить определитель Свойства определителя второго порядка, рассмотренные выше, переносятся на случай определителей любого порядка, в том числе и третьего. Минором Mi j элемента ai j определителя d n-го порядка называется определитель порядка n-1, который получается из d вычеркиванием строки и столбца, содержащих данный элемент. Алгебраическим дополнением элемента ai j определителя d называется его минор Mi j, взятый со знаком (-1) i + j. Алгебраическое дополнение элемента ai j будем обозначать Ai j. Таким образом, Ai j = (-1) i + j Mi j. Способы практического вычисления определителей, основанные на том, что определитель порядка n может быть выражен через определители более низких порядков, дает следующая теорема. Теорема (разложение определителя по строке или столбцу). Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки d = ai 1 Ai 1 + ai 2 Ai 2 +... + ai n Ai n (i=
Формулы Крамера; Система m линейных алгебраических уравнений с n неизвестными —это система уравнений вида
Здесь x1, x2, …, xn - неизвестные, которые надо определить. Коэффициенты системы a11, a12, …, amn и её свободные члены b1, b2, …, bm предполагаются известными. Индексы коэффициента aijсистемы обозначают номера уравнения i и неизвестного j,при котором стоит этот коэффициент. Система называется однородной, если все её свободные члены равны нулю, b1, b2, …, bm = 0, иначе — неоднородной Система называется квадратной, если число m уравнений равно числу n неизвестных. Решение системы уравнений - совокупность n чисел c1, c2, …cn,таких что подстановка каждого c i вместо x в систему обращает её уравнения в тождества. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если нет ни одного решения. Совместная система может иметь одно или более решений. Основными методами решения элементарных систем линейных уравнений являются метод Крамера, матричный метод и метод Гаусса.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.69.91 (0.008 с.) |

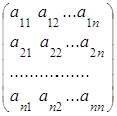
 =det A = Δ=
=det A = Δ=

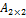 называется число, определяемое по правилу:
называется число, определяемое по правилу: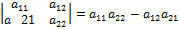 (1) т. е. определитель второго порядка есть число, равное произведению элементов главной диагонали минус произведение элементов побочной диагонали.
(1) т. е. определитель второго порядка есть число, равное произведению элементов главной диагонали минус произведение элементов побочной диагонали.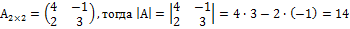
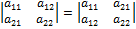
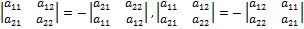

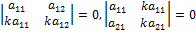
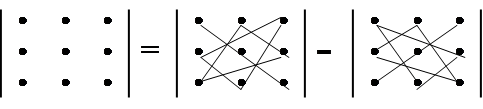
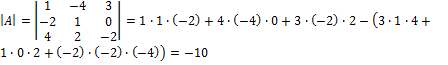
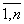 ), или j- го столбца d = a1 j A1 j + a2 j A2 j +... + anj Anj (j =
), или j- го столбца d = a1 j A1 j + a2 j A2 j +... + anj Anj (j =