
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение систем линейных уравнений методом Крамера.Содержание книги
Поиск на нашем сайте
Пусть нам требуется решить систему линейных алгебраических уравнений
Неизвестные переменные вычисляются по формулам метода Крамера как
Так находится решение системы линейных алгебраических уравнений методом Крамера. Пример. Решите систему линейных уравнений методом Крамера
Составим и вычислим необходимые определители
Находим неизвестные переменные по формулам
Ответ: x1 = 4, x2 = 0, x3 = -1. Основным недостатком метода Крамера является трудоемкость вычисления определителей, когда число уравнений системы больше трех. Вычисление математического ожидания и среднего квадратичного отклонения.
Числовые характеристики дискретных случайных величин а) Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее значений на соответствующие им вероятности, т.е.: или, если случайная величина может принимать счетное число значений, Свойства математических ожиданий Математическое ожидание постоянной величины равно этой постоянной; т.е. если С-постоянная величина, то Постоянный множитель можно выносить за символ математического ожидания, т.е. если k постоянный множитель, то Математическое ожидание суммы случайных величин равно сумме их математических ожиданий, т.е. Математическое ожидание разности случайных величин равно разности их математических ожиданий, т.е. Математическое ожидание произведения случайных величин равно произведению их математических ожиданий, т.е. 6. Если все значения случайной величины увеличить (уменьшить) на одно и тоже число С, то ее математическое ожидание увеличится (уменьшиться) на это же число б) дисперсией D(X) случайной величины Х называется математического ожидания α(M(X)= α: в) средним квадратичным отношением G(X) (G) случайной вершины называется арифметическим значением корня квадратного из дисперсии, т.е.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 159; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.255.170 (0.008 с.) |

 в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть,
в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть,  . Пусть
. Пусть  -определитель основной матрицы системы, а
-определитель основной матрицы системы, а  - определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов:
- определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов:
 .
. Решение. Основная матрица системы имеет вид
Решение. Основная матрица системы имеет вид 


 Так как определитель основной матрицы системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера.
Так как определитель основной матрицы системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера. - (определитель
- (определитель  получаем, заменив в матрице А первый столбец на столбец свободных членов
получаем, заменив в матрице А первый столбец на столбец свободных членов  , определитель
, определитель  - заменив второй столбец на столбец свободных членов,
- заменив второй столбец на столбец свободных членов,  - заменив третий столбец матрицы А на столбец свободных членов):
- заменив третий столбец матрицы А на столбец свободных членов):

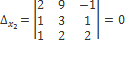 ,
, 


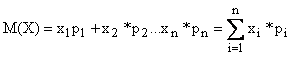
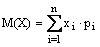 ,причем лишь в случае абсолютной сходимости ряда.
,причем лишь в случае абсолютной сходимости ряда. .
. .
. .
. .
. .
. .
. .
. .
.


