
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Министерсво транспорта Российской ФедерацииСодержание книги
Поиск на нашем сайте
МИНИСТЕРСВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Саратовский техникум железнодорожного транспорта - филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Самарский государственный университет путей сообщения» СТЖТ – филиал СамГУПС Методические указания по выполнению Контрольной работы по учебной дисциплине ЕН.01 Прикладная математика для студентов заочного обученияспециальностей: 27.02.03 Автоматика и телемеханика на транспорте (на железнодорожном транспорте), 23.02.01 Организация перевозок и управление на транспорте ( по видам), 08.02.10 Строительство железных дорог, путь и путевое хозяйство, 23.02.06 Техническая эксплуатация подвижного состава железных дорог, 13.02.07 Электроснабжение (по отраслям)
Саратов 2015 ОДОБРЕНО на заседании ЦМК «Математика, информатика и ИКТ» Протокол № ___ от «__» _____ 20__ г.
Председатель __________________ /Полкова С.И../
УТВЕРЖДАЮ Зам. директора по УР ____________________________/Моисеева Т.В./ «___» ___________20__ г. Составители: Воротилова Е.А.- преподаватель первой квалификационной категории СТЖТ - филиала СамГУПС.
Рецензенты: Внутренний Полкова С.И. - преподаватель высшей квалификационной категории СТЖТ - филиала СамГУПС
Пояснительная записка Одной из основных задач предмета «Математика» для средних специальных заведений состоит в том, чтобы вооружить студентов основами математических знаний и умений в объёме необходимом для практической деятельности, для усвоения общетехнических и специальных предметов, а также для дальнейшего повышения квалификации путём самообразования. Контрольная работа по учебной дисциплине ЕН.01 Прикладная математика проводится в соответствии с требованием рабочей программы для студентов, обучающихся на заочном отделении по специальностям: 27.02.03 Автоматика и телемеханика на транспорте (на железнодорожном транспорте), 23.02.01 Организация перевозок и управление на транспорте ( по видам), 08.02.10 Строительство железных дорог, путь и путевое хозяйство, 23.02.06 Техническая эксплуатация подвижного состава железных дорог, 13.02.07 Электроснабжение (по отраслям),с целью определения качества знаний студентов.
В результате освоения учебной дисциплины обучающийся должен уметь: - решать прикладные электротехнические задачи методом комплексных чисел; - определять основные свойства числовых функций, иллюстрировать их на графиках; - строить графики функций изученных функций, иллюстрировать по графику свойства функций; использовать понятие функции для описания и анализа зависимостей величин. - применять математические методы дифференциального и интегрального исчисления длярешения профессиональных задач; - применять основные положения теории вероятностей и математической статистики впрофессиональной деятельности; - использовать приемы и методы математического синтеза и анализа в различных профессиональных ситуациях; В результате освоения учебной дисциплины обучающийся должен знать: - основные понятия о математическом синтезе и анализе . - способы решения прикладных задач методом комплексных чисел
Требования к выполнению и оформлению контрольной работы Контрольную работу следует выполнять самостоятельно. При решении задач следует обосновывать каждый шаг решения, исходя из теоретических основ курса. Не следует применять формулы, которые не входят в программу. Решение должно быть доведено до окончательного ответа. 1. Работа выполняется в отдельной тетради школьного формата. Следует пронумеровать страницы и оставить на них поля не менее 3 смдля замечаний преподавателя. 2. На обложке тетради должны быть аккуратно записаны все данные титульного листа: шифр, специальность, если она не отражена шифре, фамилия, имя, отчество студента, предмет. 3. Каждую задачу нужно начинать с новой страницы. 4. Решение задач желательно располагать в порядке номеров, указанных в задании. 5. Условие задач должны быть обязательно записаны в тетрадь. 6. При оформлении записей в тетради необходимо выполнять общие требования к культуре их ведения. 7. Работа должна быть выполнена чернилами одного цвета, аккуратно и разборчиво. 8. Решения задач должны сопровождаться краткими, но достаточно обоснованными пояснениями, используемые формулы нужно выписывать. 9. Чертежи следует выполнять карандашом с использованием чертёжных инструментов, соблюдая масштаб.
10. В конце работы следует указать список используемых источников, поставить дату выполнения работы и подпись. 11. Если в работе допущены недочёты и ошибки, то учащийся должен выполнить все указания преподавателя, сделанные в рецензии. 12. Контрольная работа должна быть выполнена в срок (в соответствии с планом-графиком). В период сессии работы на проверку не принимаются. 13. Работа, выполненная не по своему варианту, не учитывается и возвращается студенту без оценки. 14. Учащиеся, не имеющие зачёта по контрольной работе, к экзамену не допускаются. 15. Во время экзамена зачтённые контрольные работы представляются преподавателю вместе с данными методическими указаниями. 16. Контрольная работа имеет 100 вариантов. Вариант работы выбирается по двум последним цифрам шифра согласно представленной таблице. В процессе изучения учебной дисциплины студент-заочник должен выполнить одну контрольную работу. После выполнения контрольной работы и практических заданий в сроки, предусмотренные учебным графиком, для проверки знаний студентов проводится экзамен.
Методические указания Линейная алгебра Комплексные числа. По данной теме изучите теорию. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Основные понятия и определения. Решение многих задач сводится к решению алгебраических уравнений. Поэтому исследование алгебраических уравнений является одним из важнейших вопросов математики. Стремление сделать уравнение разрешимым - одна из главных причин расширения понятия числа. Рациональные и иррациональные числа образуют множество R действительных чисел. Однако действительных чисел недостаточно для того, чтобы решить уравнение. Корень уравнения
Комплексным числом называется число видаa+bi, где aи b – действительные числа, аi - мнимая единица. Число а называется действительной частью комплексного числа, а число bi – мнимой частью. Запись комплексного числа в виде z= a+bi называется алгебраической формой записи комплексного числа. Два комплексных числа Понятия«больше» и «меньше» для комплексных чисел не определяются. Комплексные числа a+bi и a-biназываются сопряжёнными, а комплексные числаa+bi и -a-bi называются противоположными комплексными числами. Действия над комплексными числами в алгебраической форме. Суммой двух комплексных чисел Произведением комплексных чисел Вычитание комплексных чисел вводится как операция, обратная сложению; деление комплексных чисел как операция, обратная умножению. При делении на комплексное число достаточно умножить числитель и знаменатель дроби Пример 1. Найти сумму и разность комплексных чисел Решение. Сумму находим сложением двучленов
Произведение находим перемножением двучленов
Пример 2. Даны комплексные числа Решение. Разность находим вычитанием двучленов
Чтобы найти частное
Математический анализ Примеры. 1. Рассмотрим дифференциальное уравнение первого порядка Это значит, что функция y = 5 ln x– есть решение этого дифференциального уравнения. 2. Рассмотрим дифференциальное уравнение второго порядка y" - 5y' +6y = 0. Функция Действительно, Общим решением дифференциального уравнения называется функция вида График частного решения дифференциального уравнения называется интегральной кривой. Примеры 1.Найти частное решение дифференциального уравнения первого порядка xdx + ydy = 0, если y = 4 при x = 3. Решение. Интегрируя обе части уравнения, получим Замечание. Произвольную постоянную С, полученную в результате интегрирования, можно представлять в любой форме, удобной для дальнейших преобразований. В данном случае, с учётом канонического уравнения окружности произвольную постоянную С удобно представить в виде
Частное решение уравнения, удовлетворяющее начальным условиям y = 4 при x = 3 находится из общего подстановкой начальных условий в общее решение: 32 + 42= C2; C=5. Подставляя С=5 в общее решение, получим x2 +y2 = 52. Это есть частное решение дифференциального уравнения, полученное из общего решения при заданных начальных условиях. 2. Найти общее решение дифференциального уравнения
Следовательно, данное дифференциальное уравнение имеет бесконечное множество решений, так как при различных значениях постоянной С равенство
Задача, в которой требуется найти частное решение уравнения y' = f(x,y) удовлетворяющее начальному условию y(x0) = y0, называется задачей Коши. Решение уравнения y' = f(x,y), удовлетворяющее начальному условию, y(x0) = y0, называется решением задачи Коши. Решение задачи Коши имеет простой геометрический смысл. Действительно, согласно данным определениям, решить задачу Коши y' = f(x,y) при условии y(x0) = y0,, означает найти интегральную кривую уравнения y' = f(x,y) которая проходит через заданную точку M0(x0, y0). Дифференциальные уравнения первого порядка Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,y') = 0. В дифференциальное уравнение первого порядка входит первая производная и не входят производные более высокого порядка. Уравнение y' = f(x,y) называется уравнением первого порядка, разрешённым относительно производной. Общим решением дифференциального уравнения первого порядка называется функция вида Пример. Рассмотрим дифференциальное уравнение первого порядка Решением этого уравнения является функция Действительно, заменив в данном уравнении,
Следовательно, функция Найти частное решение данного уравнения, удовлетворяющее начальному условию y(1)=1 Подставляя начальные условия x = 1, y =1 в общее решение уравнения Таким образом, частное решение получим из общего Дифференциальные уравнения с разделяющимися переменными Дифференциальным уравнением с разделяющимися переменными называется уравнение вида: y'=f(x)g(y) или через дифференциалы Для тех y, для которых Уравнение вида Проинтегрировав обе части уравнения G(y) = F(x) + C – общее решение уравнения, где G(y) и F(x) – некоторые первообразные соответственно функций Признак Даламбера. Если для ряда с положительными членами Пример. Исследовать на сходимость ряд: 1) Решение: 1) Ряд сходится. 2) Ряд сходится.
Теоретический материал Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов. МИНИСТЕРСВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Саратовский техникум железнодорожного транспорта - филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования
«Самарский государственный университет путей сообщения» СТЖТ – филиал СамГУПС Методические указания по выполнению Контрольной работы по учебной дисциплине ЕН.01 Прикладная математика для студентов заочного обученияспециальностей: 27.02.03 Автоматика и телемеханика на транспорте (на железнодорожном транспорте), 23.02.01 Организация перевозок и управление на транспорте ( по видам), 08.02.10 Строительство железных дорог, путь и путевое хозяйство, 23.02.06 Техническая эксплуатация подвижного состава железных дорог, 13.02.07 Электроснабжение (по отраслям)
Саратов 2015 ОДОБРЕНО на заседании ЦМК «Математика, информатика и ИКТ» Протокол № ___ от «__» _____ 20__ г.
Председатель __________________ /Полкова С.И../
УТВЕРЖДАЮ Зам. директора по УР ____________________________/Моисеева Т.В./ «___» ___________20__ г. Составители: Воротилова Е.А.- преподаватель первой квалификационной категории СТЖТ - филиала СамГУПС.
Рецензенты: Внутренний Полкова С.И. - преподаватель высшей квалификационной категории СТЖТ - филиала СамГУПС
Пояснительная записка Одной из основных задач предмета «Математика» для средних специальных заведений состоит в том, чтобы вооружить студентов основами математических знаний и умений в объёме необходимом для практической деятельности, для усвоения общетехнических и специальных предметов, а также для дальнейшего повышения квалификации путём самообразования. Контрольная работа по учебной дисциплине ЕН.01 Прикладная математика проводится в соответствии с требованием рабочей программы для студентов, обучающихся на заочном отделении по специальностям: 27.02.03 Автоматика и телемеханика на транспорте (на железнодорожном транспорте), 23.02.01 Организация перевозок и управление на транспорте ( по видам), 08.02.10 Строительство железных дорог, путь и путевое хозяйство, 23.02.06 Техническая эксплуатация подвижного состава железных дорог, 13.02.07 Электроснабжение (по отраслям),с целью определения качества знаний студентов. В результате освоения учебной дисциплины обучающийся должен уметь: - решать прикладные электротехнические задачи методом комплексных чисел; - определять основные свойства числовых функций, иллюстрировать их на графиках; - строить графики функций изученных функций, иллюстрировать по графику свойства функций; использовать понятие функции для описания и анализа зависимостей величин. - применять математические методы дифференциального и интегрального исчисления длярешения профессиональных задач; - применять основные положения теории вероятностей и математической статистики впрофессиональной деятельности; - использовать приемы и методы математического синтеза и анализа в различных профессиональных ситуациях; В результате освоения учебной дисциплины обучающийся должен знать: - основные понятия о математическом синтезе и анализе . - способы решения прикладных задач методом комплексных чисел
Требования к выполнению и оформлению контрольной работы Контрольную работу следует выполнять самостоятельно. При решении задач следует обосновывать каждый шаг решения, исходя из теоретических основ курса. Не следует применять формулы, которые не входят в программу. Решение должно быть доведено до окончательного ответа. 1. Работа выполняется в отдельной тетради школьного формата. Следует пронумеровать страницы и оставить на них поля не менее 3 смдля замечаний преподавателя. 2. На обложке тетради должны быть аккуратно записаны все данные титульного листа: шифр, специальность, если она не отражена шифре, фамилия, имя, отчество студента, предмет. 3. Каждую задачу нужно начинать с новой страницы. 4. Решение задач желательно располагать в порядке номеров, указанных в задании. 5. Условие задач должны быть обязательно записаны в тетрадь. 6. При оформлении записей в тетради необходимо выполнять общие требования к культуре их ведения. 7. Работа должна быть выполнена чернилами одного цвета, аккуратно и разборчиво. 8. Решения задач должны сопровождаться краткими, но достаточно обоснованными пояснениями, используемые формулы нужно выписывать. 9. Чертежи следует выполнять карандашом с использованием чертёжных инструментов, соблюдая масштаб. 10. В конце работы следует указать список используемых источников, поставить дату выполнения работы и подпись. 11. Если в работе допущены недочёты и ошибки, то учащийся должен выполнить все указания преподавателя, сделанные в рецензии. 12. Контрольная работа должна быть выполнена в срок (в соответствии с планом-графиком). В период сессии работы на проверку не принимаются. 13. Работа, выполненная не по своему варианту, не учитывается и возвращается студенту без оценки. 14. Учащиеся, не имеющие зачёта по контрольной работе, к экзамену не допускаются. 15. Во время экзамена зачтённые контрольные работы представляются преподавателю вместе с данными методическими указаниями. 16. Контрольная работа имеет 100 вариантов. Вариант работы выбирается по двум последним цифрам шифра согласно представленной таблице. В процессе изучения учебной дисциплины студент-заочник должен выполнить одну контрольную работу. После выполнения контрольной работы и практических заданий в сроки, предусмотренные учебным графиком, для проверки знаний студентов проводится экзамен.
Методические указания
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 129; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.185.214 (0.015 с.) |

 или
или  называется мнимой единицей и обозначается буквой i. Таким образом, символ i удовлетворяет условию
называется мнимой единицей и обозначается буквой i. Таким образом, символ i удовлетворяет условию
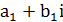 и
и  называются равнымитогда и только тогда, когда равны их действительные части и коэффициенты при мнимой части.
называются равнымитогда и только тогда, когда равны их действительные части и коэффициенты при мнимой части. и
и  называется комплексное число
называется комплексное число  .
.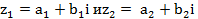 называется комплексное число.
называется комплексное число. на число сопряжённое знаменателю
на число сопряжённое знаменателю 
 и
и  .
. :
:
 с последующей заменой
с последующей заменой  на -1.
на -1.
 и
и  . Найти разность
. Найти разность  и частное
и частное  .
. и
и  :
: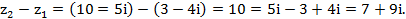
 :
:
 Решением этого уравнения является функция y = 5 ln x. Действительно,
Решением этого уравнения является функция y = 5 ln x. Действительно,  , подставляя y' в уравнение, получим
, подставляя y' в уравнение, получим  – тождество.
– тождество. – решение этого уравнения.
– решение этого уравнения. . Подставляя эти выражения в уравнение, получим:
. Подставляя эти выражения в уравнение, получим:  ,
,  – тождество. А это и значит, что функция
– тождество. А это и значит, что функция  – есть решение этого дифференциального уравнения.
– есть решение этого дифференциального уравнения. ,в которую входит столько независимых произвольных постоянных, каков порядок уравнения. Частным решением дифференциального уравнения называется решение, полученное из общего решения при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находится при определённых начальных значениях аргумента и функции.
,в которую входит столько независимых произвольных постоянных, каков порядок уравнения. Частным решением дифференциального уравнения называется решение, полученное из общего решения при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находится при определённых начальных значениях аргумента и функции.
 .
. - общее решение дифференциального уравнения.
- общее решение дифференциального уравнения. Решением этого уравнения является всякая функция вида
Решением этого уравнения является всякая функция вида  , где С – произвольная постоянная. Действительно, подставляя в уравнения
, где С – произвольная постоянная. Действительно, подставляя в уравнения  ,
,  .
. . Например, непосредственной подстановкой можно убедиться, что функции
. Например, непосредственной подстановкой можно убедиться, что функции  являются решениями уравнения
являются решениями уравнения  , которая содержит одну произвольную постоянную.
, которая содержит одну произвольную постоянную. .
. .
. его значением, получим
его значением, получим
 то есть 3x=3x
то есть 3x=3x откуда C = 0.
откуда C = 0.
 – частное решение.
– частное решение. , где f(x) и g(y) – заданные функции.
, где f(x) и g(y) – заданные функции. , уравнение y'=f(x)g(y) равносильно уравнению,
, уравнение y'=f(x)g(y) равносильно уравнению,  в котором переменная y присутствует лишь в левой части, а переменная x- лишь в правой части. Говорят, «в уравнении y'=f(x)g(y разделим переменные».
в котором переменная y присутствует лишь в левой части, а переменная x- лишь в правой части. Говорят, «в уравнении y'=f(x)g(y разделим переменные». и f(x), C - произвольная постоянная.
и f(x), C - произвольная постоянная. выполняется условие
выполняется условие  , то ряд сходится при l<1 и расходится при l>1.. Признак Даламбера не дает ответа, если l=1 этом случае для исследования ряда применяются другие методы.
, то ряд сходится при l<1 и расходится при l>1.. Признак Даламбера не дает ответа, если l=1 этом случае для исследования ряда применяются другие методы. ; 2)
; 2)  ; 3)
; 3) 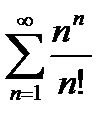 ;
;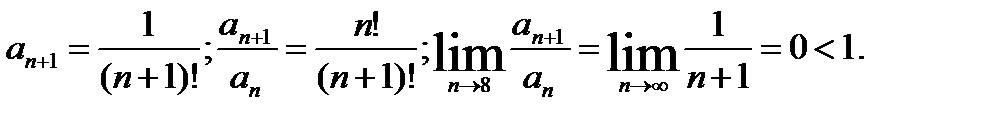

 Ряд расходится.
Ряд расходится.


