Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Евклидовы пространства. Норма вектора. Ортонормированный базис. Процесс ортогонализации. Неравенство Коши-Буняковского.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность равную 3. В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов, определённых ниже. Обычно 1. Конечномерное гильбертово пространство, то есть конечномерное вещественное векторное пространство
в простейшем случае (евклидова норма):
где 2. Метрическое пространство, соответствующее пространству описанному выше. То есть
где 3. Вообще любое предгильбертово пространство (пространство со скалярным произведением Норма вектора Норма в векторном пространстве 1. 2. 3. Эти условия являются аксиомами нормы. Векторное пространство с нормой называется нормированным пространством, а условия (1-3) — также аксиомами нормированного пространства. Нетрудно видеть, что из аксиом нормы вытекает свойство неотрицательности нормы:
Действительно: Из 3 получаем, что
Любой ненулевой вектор Ортонормированный базис удовлетворяет еще и условию единичности нормы всех его элементов. То есть это ортогональный базис с нормированными элементами. Последнее удобно записывается при помощи символа Кронекера:
9.Линейные операторы. Их свойства и действия над ними. Обратный оператор. Преобразование матрицы линейного оператора. Подобные матрицы. Линейным преобразованием (линейным оператором) линейного пространства Поскольку линейное преобразование является частным случаем линейного отображения, к нему применимы все понятия и свойства, рассмотренные для отображений: инъективность, сюръективность, биективность, обратимость, ядро, образ, дефект, ранг и т.д. Матрицей линейного оператора (преобразования) Матрица биективного линейного оператора (преобразования) обратима, т.е. невырождена. Поэтому биективное (обратимое) преобразование называют также невырожденным. Линейные операторы в евклидовом пространстве. Сопряженные и самосопряженные операторы. Собственные векторы и собственные значения. Канонический вид матрицы. Операторы в евклидовом пространстве и их продолжение на комплексификацию. В евклидовом пространстве для оператора 9 определяется сопряженный оператора 10 той же формулой 11 при любых х и у, что и в унитарном пространстве. Доказательство существования и единственности сопряженного оператора ничем не отличается от аналогичных доказательств для унитарного пространства. Матрица оператора 12 в ортонормальном базисе просто транспонирована с матрицей оператора 13 При продолжении взаимно сопряженных операторов 14 с S на 15 они останутся сопряженными. Действительно,
Нормальные операторы в евклидовом пространстве. Нормальный оператор 16 в евклидовом пространстве S остается нормальным и при его продолжении на комплексификацию 17 пространства S. Поэтому в S существует ортонормальный базис из собственных векторов, диагонализующий матрицу оператора А. Для вещественных собственных значений можно взять вещественные собственные векторы, т. е. лежащие в S. Действительно, координаты собственных векторов относительно базиса 18 определяются из линейных однородных уравнений с вещественными коэффициентами в случае вещественности собственного значения.
Комплексные собственные значения появляются парами сопряженных с одинаковой кратностью. Выбрав ортонормальный базис из собственных векторов, принадлежащих некоторому собственному значению 19 при 20 базис из собственных векторов для собственного значения 21 можно взять из векторов, сопряженных с векторами базиса собственных значений для X. Такой базис будет ортонормальный. Теперь натянем на каждую пару и 22 сопряженных векторов двумерное комплексное подпространство.
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 927; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.67.57 (0.011 с.) |

 -мерное евклидово пространство обозначается
-мерное евклидово пространство обозначается  , хотя часто используется не вполне приемлемое обозначение
, хотя часто используется не вполне приемлемое обозначение  .
. ,
,
 (в евклидовом пространстве всегда можно выбрать базис, в котором верен именно этот простейший вариант).
(в евклидовом пространстве всегда можно выбрать базис, в котором верен именно этот простейший вариант). с метрикой, введённой по формуле:
с метрикой, введённой по формуле:
 и
и  .
. ).
). над полем вещественных или комплексных чисел — это функционал
над полем вещественных или комплексных чисел — это функционал 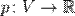 , обладающий следующими свойствами:
, обладающий следующими свойствами: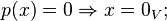
 (неравенство треугольника);
(неравенство треугольника);

 Теперь из 2 получаем
Теперь из 2 получаем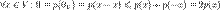 . Таким образом,
. Таким образом, 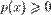 .
. . В частности,
. В частности, 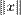 — это норма элемента
— это норма элемента  векторного пространства
векторного пространства 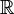 .
.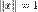 ) называется нормальным или нормированным.
) называется нормальным или нормированным.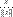 имеет единичную норму. С геометрической точки зрения это значит, что мы берем сонаправленный вектор единичной длины.
имеет единичную норму. С геометрической точки зрения это значит, что мы берем сонаправленный вектор единичной длины.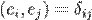
 называется линейное отображение
называется линейное отображение  пространства
пространства  в базисе
в базисе  пространства
пространства 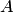 , составленная из координатных столбцов образов базисных векторов
, составленная из координатных столбцов образов базисных векторов  , найденных относительно базиса
, найденных относительно базиса 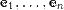 .
.