
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы теории множеств и математической логики. Действительные числа. Грани. Понятие функции. Обратная функция.Содержание книги
Поиск на нашем сайте
Числовые множества задаются на оси действительных чисел R. На этой оси выбирают масштаб и указывают начало отсчета и направление. Наиболее распространенные числовые множества:
Кантор описывает множество следующим образом: Множество Грани. Множество всех рациональных чисел является счетным множеством. Счетным является множество всех точек плоскости (пространства) имеющих рациональные координаты. Множество всех действительных чисел является несчетным: оно имеет мощность, называемую континуумом. Некоторое непустое подмножество Всякое число Непустое подмножество В противоположность этому определению, множество Множество, неограниченное как сверху, так и снизу, называется неограниченным множеством. Наименьшую из верхних граней непустого подмножества множества действительных чисел Примем без доказательства утверждение о том, что всякое ограниченное сверху (снизу) множество имеет точную верхнюю (нижнюю) грань. Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Понятие последовательности и ее предела. Бесконечно малые. Свойства пределов. Монотонные последовательности. Число «е». Числовой последовательностью называется числовая функция, определенная на множестве натуральных чисел. Если функцию Задают последовательность обычно либо перечислением ее элементов Бесконечный предел Наряду с бесконечно малыми существуют и бесконечно большие величины, являющиеся обратными по отношению к бесконечно малым. Поэтому Говорят, что предел последовательности В отличие от бесконечно малых последовательностей, бесконечно большие могут не иметь предела. Например, Свойства пределов: Пределы обладают следующими свойствами: - Если - Если существуют - Если существуют - Если существуют - Если существуют - Если Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств. Последовательность из одного числа не может считаться возрастающей или убывающей. Число «e» — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.254.35 (0.008 с.) |

 ‑ множество натуральных чисел;
‑ множество натуральных чисел; ‑ множество целых чисел;
‑ множество целых чисел;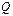 – множество рациональных или дробных чисел;
– множество рациональных или дробных чисел; ‑ множество действительных чисел.
‑ множество действительных чисел. есть любое собрание определенных и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое. Эти объекты называются элементами множества
есть любое собрание определенных и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое. Эти объекты называются элементами множества  .
. множества действительных чисел называют ограниченным сверху (снизу), если существует действительное число
множества действительных чисел называют ограниченным сверху (снизу), если существует действительное число  такое, что
такое, что 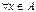 выполняется неравенство
выполняется неравенство  (
( ).
). .
. множества действительных чисел называется ограниченным, если оно ограничено и сверху и снизу.
множества действительных чисел называется ограниченным, если оно ограничено и сверху и снизу. мы бы не предложили в качестве верхней (нижней) границы множества
мы бы не предложили в качестве верхней (нижней) границы множества  называют точной верхней гранью этого множества и обозначают sup
называют точной верхней гранью этого множества и обозначают sup  . Наибольшую из нижних граней непустого подмножества множества действительных чисел
. Наибольшую из нижних граней непустого подмножества множества действительных чисел  называют точной нижней гранью этого множества и обозначают inf
называют точной нижней гранью этого множества и обозначают inf  задать на множестве натуральных чисел
задать на множестве натуральных чисел  , то множество значений функции будет счетным и каждому номеру
, то множество значений функции будет счетным и каждому номеру  ставится в соответствие число
ставится в соответствие число  . В этом случае говорят, что задана числовая последовательность. Числа
. В этом случае говорят, что задана числовая последовательность. Числа 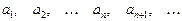 называют элементами или членами последовательности, а число
называют элементами или членами последовательности, а число  – общим или
– общим или  –м членом последовательности. Каждый элемент
–м членом последовательности. Каждый элемент 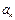 имеет последующий элемент
имеет последующий элемент  . Это объясняет употребление термина «последовательность».
. Это объясняет употребление термина «последовательность». , либо указанием закона, по которому вычисляется элемент с номером
, либо указанием закона, по которому вычисляется элемент с номером  , т.е. указанием формулы ее
, т.е. указанием формулы ее  ‑го члена
‑го члена 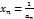 является бесконечно большой (
является бесконечно большой (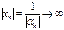 , при
, при  ), если
), если 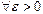
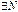 такое, что при
такое, что при 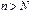
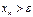 .
.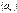 равен
равен 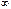 , если для
, если для 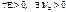 такое, что
такое, что 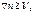 выполняется неравенство:
выполняется неравенство:  .
.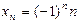 по модулю неограниченно растет, но сама величина
по модулю неограниченно растет, но сама величина 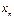 не имеет определенного стремления.
не имеет определенного стремления. – есть постоянная функция, то
– есть постоянная функция, то 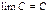 ;
; , и в некоторой окрестности точки
, и в некоторой окрестности точки 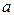 функция
функция 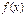 ограничена, т.е.
ограничена, т.е.  , тогда
, тогда  ;
;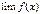 и
и  при каком-то условии, то
при каком-то условии, то 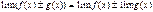 (при том же условии). Это свойство справедливо для любого конечного числа функций;
(при том же условии). Это свойство справедливо для любого конечного числа функций; и
и 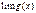 при каком-то условии, то
при каком-то условии, то 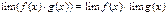 (при том же условии). Это свойство также справедливо для любого конечного числа функций, в частности, справедлива формула
(при том же условии). Это свойство также справедливо для любого конечного числа функций, в частности, справедлива формула 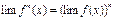 ;
;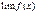 и
и 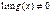 при каком-то условии, то
при каком-то условии, то 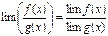 (при том же условии);
(при том же условии);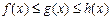 и существуют
и существуют 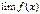 ,
, 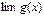 и
и  , то
, то 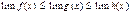 .
.


